В) бесконечная равномерно заряженная плоскость.

3

арядовое состояние поверхностных объектов характеризуется поверхностной плотностью  заряда, которая в случае равномерного заряжения численно равна  = q/S - заряду, приходящемуся на единицу площади заряженной поверхности.

У равномерно заряженной бесконечной плоскости силовые ли­нии обязаны быть перпендику­лярны плоскости, поэтому в качестве замкнутой поверхности, через которую вычисляется поток вектора в теореме Остроградского - Гаусса, целесообразно выбрать цилиндр, ось которого пер­пендикулярна плоскости, а основания равноудалены от нее. Вычислим поток вектора от плос­кости с поверхностной плот­ностью заряда  через замкнутую поверхность цилиндра, расположен­ного симметрично - перпендикулярно заряженной плоскости:

= = = = 2ЕS_осн

Также как и в случае с заряженной нитью, замкнутую цилинд­рическую поверхность разби­ваем на боковую поверхность и поверх­ность двух оснований, причем, здесь поток вектора через боковую поверхность будет равным нулю, т. к. вектор параллелен оси цилин­дра и лишь скользит вдоль его боковой поверхности, не пронизывая её. При вычислении же потока через основания цилиндра учтено, что век­тор перпендикулярен к ним, и его проекция на внешнюю нормаль к ним совпадает с самим модулем вектора , то есть Е_n = Е. Все точки поверхности оснований являются электрически экви­валентными, поэтому вектор в них сохраняет постоянное значение и напряженность Е может быть вынесена за знак интеграла при вычислении потока . Оба основания являются электрически эквивалентными, и поток вектора через них равен удвоенному значе­нию потока через одно из них.

Внутрь выбранной цилиндрической поверхности попадет заряд q_, равный S_осн. Записывая теорему Остроградского - Гаусса для данной поверхности, выразим из нее напряженность ЭСП рав­номерно заряженной бесконечной плоскости, а затем и разность потенциалов (и потенциал):

= = 2ЕS_осн = q_ = S_осн  Е = /2_о = const. Так как ЭСП – однородное, то ₁ - ₂ = (х₂ - х₁)/2_о   = - х/2_о + const.

Для наглядности изобразим зависимость Е и  от удаления х от заряженной плоскости на рис. Э

СП бесконечной равномерно заряженной плоско­сти является настолько сильным, что его напряжен­ность не убывает с удалением х от плоскости, сохраняя постоянное значение: Е = /2_о = const. Саму плос­кость можно представлять как составленную из множества заряженных нитей, а ее ЭСП - как супер­пози­цию полей нитей.

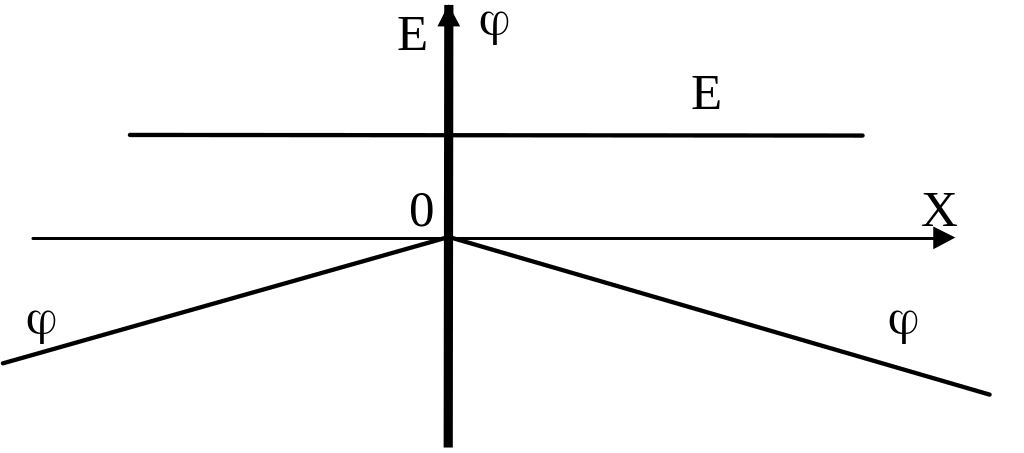
Т. к. Е = соnst и Е = - d/dх - есть пространственная производная со знаком минус от потен­циала, то потенциал должен быть линейно убывающей функцией расстояния от плоскости с отрица­тельными значениями: Е = соnst  означает постоянство быстроты убыли потенциала при удалении от нити.