Б) бесконечно длинная прямолинейная нить (цилиндр).

Основной характеристикой зарядового состояния линейно протяженных объектов (нити, про­вода, цилиндра и т. п.) является линейная плотность заряда , которая, в случае равномерного заря­жения, численно равна заряду, приходящемуся на единицу длины объекта. Осевая (аксиальная) гео­метрическая симметрия прямолинейных заряженных объектов порождает, при условии равно­мер­ного заряжения, соответствующую электрическую симметрию, т. е. осевую симметрию ЭСП, созда­ваемого такими объектами. Поэтому в качестве замкнутой поверхности интегрирования для тео­ремы Остроградского - Гаусса в применении к таким объектам целесообразно выбрать цилинд­риче­скую поверхность, соосную (коаксиальную) с заряженным объектом.

О

кружим отрезок равномерно заряженного проводника длиной l цилиндрической поверхно­стью радиусом r и вычислим поток вектора че­рез эту поверхность. Вследствие радиально-осевой симметрии источника и самого ЭСП, его силовые линии перпендикулярны к боковой поверхности цилиндра и скользят вдоль его оснований, не про­низывая их. Все точки боковой поверхности явля­ются электрически эквивалентными, т. е. числен­ное значение напряженности Е в них имеет одно и то же значение. Поток вектора через ука­занную цилиндрическую поверхность S_ц может быть расписан следующим образом:

Ф_Е = = = + = = = ЕS_бок = Е2rl

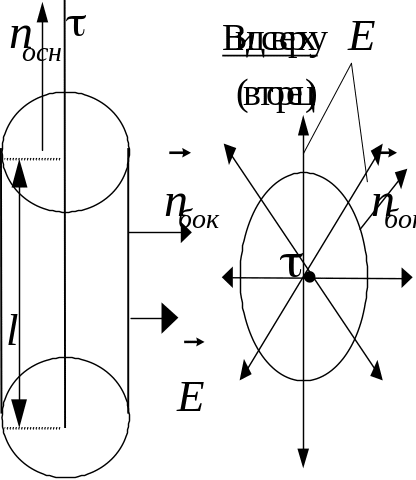
Полная (замкнутая) поверхность S_ц цилиндра высотой h и радиусом основания r разбивается при вычислении потока вектора через нее на боковую поверхность S_бок и поверхность S_осн двух оснований.

Т. к. вектор скользит вдоль оснований, его поток через них равен нулю. При вычислении же потока вектора через боковую поверхность цилиндра учтено, что вектор перпендикулярен боковой поверхности, т. е. его проекция на нормаль к ней равна самому численному значению Е. Учтено также, что во всех точках боковой поверхности значение напряженности Е постоянно, ее можно вынести за знак интеграла.

Полученное значение потока вектора приравниваем, в соответствии с теоремой Остроград­ского - Гаусса, к суммарному заряду, находящемуся внутри замкнутой цилиндрической поверхности, деленному на _о. Внутрь цилиндра высотой h попадает заряд q_,, равный q_ = h. Приравнивая обе части теоремы Остроградского - Гаусса, выразим напряженность Е поля равномерно заряженной нити:

= = Е2rl = q_ = h  Е = /(2_оr) = 2k/r (k = 1/4_о)

Как видно из полученного выражения, напряженность ЭСП равномерно заряженной нити (цилиндра) убывает гиперболически с удалением от нити, т. е. медленнее, чем напряженность Е точечного заряда или равномерно заряженной сферы. Это связано с тем, что при осевой симметрии силовые линии не так быстро расходятся (рассеиваются) с удалением от источника ЭСП, как при сферической симметрии, характерной для точечного заряда и равномерно заряженной сферы. Боль­шую «мощность» ЭСП нити по сравнению с точечным зарядом можно объяснить также тем, что нить представляет собой линейно упорядоченную совокупность точек, то есть, ее ЭСП есть множе­ство ЭСП составляющих ее точек.

Применительно к цилиндру (трубе) полученная формула справедлива лишь в наружной области, то есть при r  R, где R – радиус цилиндра (трубы). Во внутренней же области цилиндра (как и сферы), то есть при r  R, поля нет, его напряженность Е = 0.

Из полученного выражения для напряженности, получим выражение для потенциала и разно­сти потенциалов ЭСП равномерно заряженной бесконечно длинной нити (цилиндра):

₁ - ₂ = = = (2k/) = (2k/)(lnr₂ - lnr₁) = (2k/)lnr₂/r₁ 

 = - (2k/)lnr + const; при r  ,   0

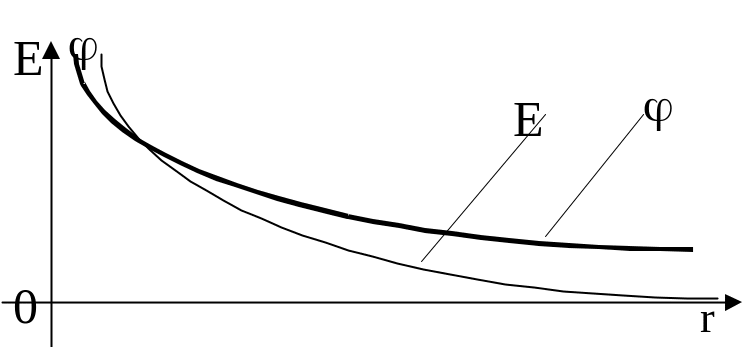
Для наглядности зависимости Е и  от радиаль­ного удаления r от нити изображены на рис. Отметим, что понятие потенциала, вследствие своей неодно­значно­сти, оказывается недоста­точно адекватной ха­рактеристи­кой ЭСП протяженных источников.