Знаходження параметрів криволінійної кореляційної залежності

Припустимо, що на основі результатів випробувань виникла гіпотеза, що

пов”язані квадратичною кореляційною залежністю, тобто

( 43 )

А) Якщо спостерігалось n різних пар , то метод найменших квадратів полягає в мінімізації функції (34) і дає систему рівнянь (35) відносно параметрів a, b, c. Після ділення обох частин кожного рівняння на n отримуємо

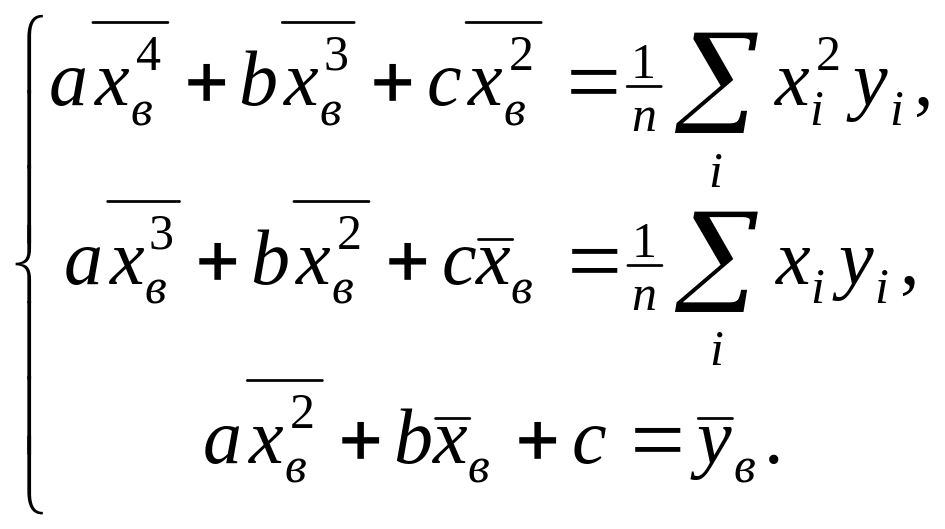( 44 )

В) В загальному випадку розглядаємо задачу на мінімум функції

( 45 )

система рівнянь для знаходження a, b, c має вигляд

( 46 )

або після почленного ділення кожного рівняння на n і деяких перетворень в правих частинах

( 47 )

Поняття про множинну кореляцію

Якщо вивчається кореляційна залежність між більш ніж двома випадковими величинами, кажуть про множинну кореляцію. Ми обмежимось трьома випадковими величинами .

Умовне математичне сподівання випадкової величини за умови, що випадкова величина набула значення x, а - y,

,

називається функцією реґресії на . Аналогічно запроваджують функції реґресії на та на відповідно. Функції реґресії визначають залежність між значеннями двох випадкових величин і відповідними середніми значеннями іншої.

Поруч з функціями реґресії розглядають умовні математичні сподівання однієї випадкової величини за умови, що інша набуває певне значення, а значення третьої фіксоване. Наприклад, - математичне сподівання випадкової величини за умови, що набуває значення x, а значення фіксоване і дорівнює y. Аналогічний сенс мають величини , , які характеризують, поруч з , залежність між двома випадковими величинами при фіксованих значениях третьої.

Задачі множинної кореляції.

1. Визначення вигляду кореляційної залежності між випадковими величинами.

2. Оцінка тісноти зв”язку між двома випадковими величинами та третьою, яка залежить від них.

3. Оцінка тісноти зв”язку між кожними двома випадковими величи­нами при фіксованих значеннях третьої.

Результати n незалежних випробувань над трьома випадковими величинами задаються системою таблиць, кожна з яких фіксує, наприклад, кількість спостережених пар при даному значенні . Як достатньо загальний приклад розглянемо систему таблиць (таблиця 10). З таблиці 10 можна перш за все отримати варіаційні ряди для кожної з складових (див. таблицю 11) та оцінити їх числові характеристики .

Далі, для кожної пари випадкових величин можна скласти кореляцій­ні таблиці (таблиця 12) та оцінити коефіцієнти кореляції .

Таблиця 10. Множинна кореляція

	3			3	3	1		4	1	3		4
	5	1	4	10	5	2	1	8	4	3		7
			3	3			4	4		2	5	7
	8	1	7	16	8	3	5	16	5	8	5	18

Таблиця 11. Варіаційні ряди для складових (n = 50)

	21	12	17		11	25	14		16	16	18

Таблиця 12. Кореляційні таблиці

7 4 11 14 6 5 25 2 12 14 21 12 17 n=50

3 4 4 11 10 8 7 25 3 4 7 14 16 16 18 n=50

8 1 7 16 8 3 5 16 5 8 5 18 21 12 17 n=50

Нехай вивчається лінійна кореляційна залежність між і , тобто припускається, що рівняння реґресії на має вигляд

,

і треба знайти значення параметрів A, B, C. З цією метою використовується метод найменших квадратів, причому для зручності функція лінійної реґресії шукається у вигляді

. ( 48 )

Задля спрощення припустимо ще, що в результаті n випробувань отримано n різних трійок значень , а саме . Тоді значенням відповідають: а) значення , б) значення . Отже, йдеться про мінімізацію такої функції

( 49 )

Після ділення обох частин кожного рівняння на n маємо (для скорочення запису ми опускаємо індекс в (вибірковий) в наступних числових характеристиках випадкових величин)

( 50 )

Тіснота лінійної залежності між і оцінюється сукупним коефіцієнтом кореляції

, ( 51 )

причому .

Тіснота лінійної залежності між і (при фіксованому ), а також між і (при фіксованому ) оцінюється частинними коефіцієнтами кореляції

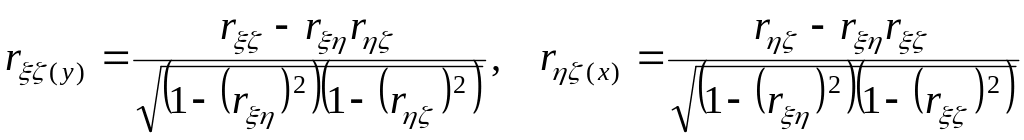( 52 )

Якщо, наприклад, , то вплив на випадкову величину з боку більше, ніж з боку .

Приклад 7 (див. [7, стор. 104, приклад 35]) Кільця підшипників піддаються попередньому і остаточному шліфуванню на двох безцентровошліфувальних верстатах. Статистичними дослідженнями встановлено, що овальність після попереднього шліфування, припуск під остаточне шліфування і овальність після остаточного шліфування характеризуються наступними показниками (все в мм).

На підставі формул (48), (50) параметри a, b і вибіркове (статистичне) рівняння лінійної реґресії на ,

,

.

Сукупний коефіцієнт кореляції згідно з формулою (51) дорівнює

Він є достатньо великим і свідчить про наявність помітної лінійної залежності між і . За формулами (52) знаходимо частинні коефіцієнти кореляції

,

і помічаємо, що вплив овальності після попереднього шліфування сильніше припуска під остаточне шліфування, бо зв”язок між і сильніше, ніж між і . Це ж саме випливає з аналізу отриманого рівняння реґресії на , . Якщо значення y збільшити вдвічі при фіксованому , то збільшиться на 5.75 %; якщо ж вдвічі збільшити x при фіксованому , то збільшиться на 94 %. Звідси випливає велике значення доброї роботи при виконанні першої операції – попереднього шліфування.