Кореляційний момент і коефіцієнт кореляції

Відомо, що для двох випадкових величин дисперсія їх суми дорівнює

Величина

( 8 )

називається кореляційним моментом, а безрозмірна величина

( 9 )

- коефіцієнтом кореляції випадкових величин .

Якщо дискретні, то

( 10 )

Для неперервних випадкових величин

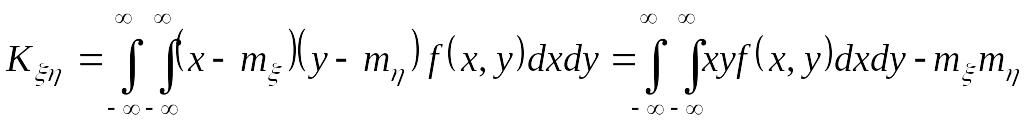( 11 )

Якщо випадкові величини незалежні, то . Обернене твердження, взагалі кажучи, не є вірним: якщо, наприклад, , то і можуть бути залежними.

Випадкові величини (може, залежні), кореляційний момент (чи коефіцієнт кореляції) яких дорівнює нулю, називаються некорельованими (незв”язни-ми). Якщо випадкові величини незалежні, то вони некорельовані, але не навпаки.

Приклад 2. Для розглянутого в прикладі 1 загального нормального розподілу на площині с щільністю розподілу (7) формули (9), (11) дають

,

тобто параметр r є коефіцієнтом кореляції складових . Ми бачимо, що при складові незалежні. Якщо, навпаки, незалежні, то . Отже, для загального нормального розподілу на площині некорельованість складових збігається з їх незалежністю. Для інших двовимірних випадкових величин це, взагалі кажучи, не так.

Відомо, що

.

Якщо, далі, пов”язані линійною залежністю то . Наприклад, якщо , то при , при . Звідси випливає, що коефіцієнт кореляції є мірою лінійної залежності між двома випадковими величинами.

Кореляційне відношення

Кореляційним відношенням випадкової величини до випадкової величини (відповідно ) називається величина

( 12 а ) 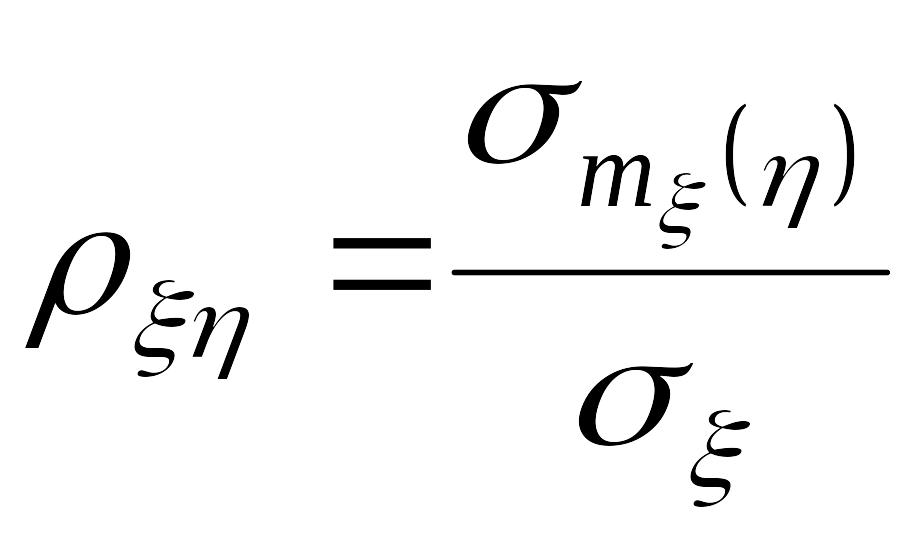( 12 б )

Можна довести, що

причому , якщо пов”язані функціональною (не обов”язково лінійною) залежністю. Інакше кажучи, кореляційне відношння є мірою функці-о­нальної залежності між двома випадковими величинами. Проте, засвідчуючи наявність функціональної залежності, воно нічого не каже про самий вигляд цієї залежності.

Кореляційне відношення двох випадкових величин вперше ввів в розгляд англійський статистик, біолог і філософ Карл Пірсон /1857 - 1936/.

Лінійна кореляція

Нехай функції реґресії лінійні, тобто між випадковими величинами має місце лінійна кореляція. Тоді, як можна показати (див., наприклад, [2, с. 197]),

Рівняння (лінійної) реґресії на і на

( 13 а ) ( 13 б )

Відповідні їм прямі реґресії (рис. 2) перетинаються в точці , мають кутові кеэфіцієнти

, ( 14 )

з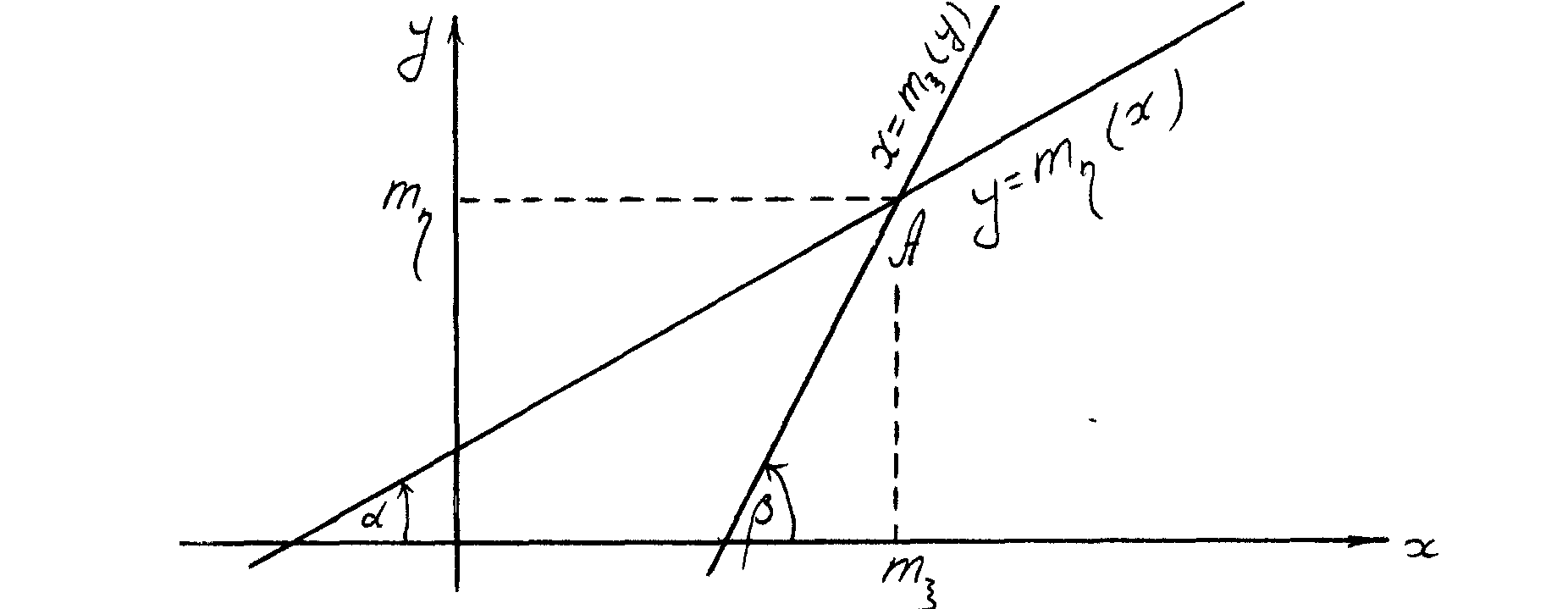 бігаються при (якщо та пов”язані линійною функціональ­ною залежністю), перпендикулярні осям відповідно при , то-бто у випадку некорельованості та . Рис. 2. Прямі реґресії Приклад 3. Для загального нормального розподілу на площині (приклади 1, 2) складові та пов”язані, як показано вище, лінійною кореляційною залежністю.

Статистичні оцінки параметрів кореляційної залежності

Нехай над двовимірною випадковою величиною здійснено n незалежних випробувань та їх результати представлено таблицею

Таблиця 1. Результати випробувань

			...
			...
			...
...	...	...	...	...	...
			...
			...

Значення, набуті випадковими величинами , сгруповані по интервалах, - кількість значень , які потрапили в i-й інтервал ; - кількість значень , які потрапили в j-й інтервал ; - кількість пар значень , які потрапили в i-й інтервал значень та j-й інтервал значень . Оскільки використання інтервалів в наступних розрахунках незручне, вчиняють таким же чином, як сказано в методичці [6], а саме в кожному з інтервалів беруть значення величини (або просто серединну точку), рівне , а в кожному з інтервалів - значение (або серединну точку), рівне , і вважають, що пара з”явилася раз. Отримують таблицю (кореляційну таблицю) 2, яку звичайно використовують в розрахунках. Часто-густо результати випробувань над одразу оформляють таблицею 2.

Таблиця 2. Кореляційна таблиця

			...		...
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
			...		...

Для більшої зручності розрахунків можна замінити частоту появи кожної пари значень відповідною відносною частотою (таблиця 3).

Таблиця 3. Кореляційна таблиця

			...		...
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
			...		...		1

Таблиці 2, 3 дозволяють перш за все отримати дискретні варіаційні ряди для кожної з випадкових величин (складових двовимірної випадкової величини ) (див. таблицю 4) та оцінити їх математичні сподівання, дисперсії й середні квадратичні відхилення:

Таблиця 4. Варіаційні ряди для складових

			...					...
			...					...
			...					...

а) вибіркові (статистичні) середні

, ( 15 )

б) вибіркові (статистичні) дисперсії

, ( 16 )

в) вибіркові (статистичні) середні квадратичні відхилення

, ( 17 )

г) виправлені дисперсії та середні квадратичні відхилення

( 18 )

Детальніше див. нашу методичку [6].

Значення функції реґресії в точці оцінюється так званим умовним середнім , яке отримують з формули (4а) для умовного математичного сподівання заміною умовної ймовірності відповідною умовною відносною частотою , тобто відносною частотою події за умови, що відбулася подія . Отже,

. ( 19 )

Оскільки за означенням умовної відносної частоти

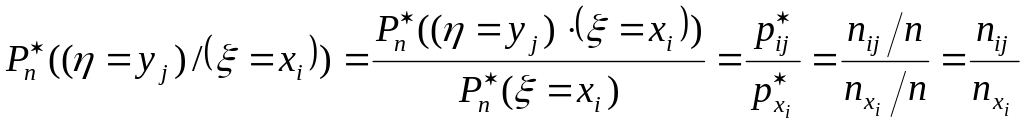, ( 20 )

формулу (19) можна подати в двох різних формах залежно від використання кореляційної таблиці 2 або 3. Якщо послуговуються таблицею 2, то на підставі однієї частини формули (20)

. ( 21 а )

Формула свідчить, що умовне середнє є середнім арифметичним тих значень випадкової величини , які спостерігались разом з значенням .

При послуговуванні таблицею 3 інша частина формули (20) дає

. ( 21 б)

Аналогічним умовним середнім оцінюється значення функції реґ­ресії в точці ,

( 22 а )

, ( 22 б )

- середнім арифметичним тих значень випадкової величини , які спостерігались разом з значенням .

Кореляційний момент випадкових величин можна оцінити вибірковим (статистичним) кореляційним моментом

( 23 )

де сума береться по всіх парах .

Формулу (23) можна подати в дещо простішому вигляді, позначаючи кожну пару значений величин єдиним індексом,

( 23 а )

де - відносна частота (відповідно кількість) появ пари , а сума береться по всіх різних парах.

Якщо припустити, що кожна пара зустрічається по одному разу, отримуємо ще більш просту формулу

. (23 б)

Само вона найчастіше зустрічається в теоретичних дослідженнях.

Формули (23), (23 а), (23 б) дають зміщену оцінку кореляційного момента, оскільки

Незміщеною оцінкою є виправлений кореляційний момент

(24)

Наприклад, для випадку формули (23 а), коли кожна пара значений величин позначається єдиним індексом, отримуємо

( 25 )

Коефіцієнт кореляції можна оцінити вибірковим (статистичним) коефіцієнтом кореляції

( 26 )

Для оцінки кореляциійних відношень використовуються формули

( 27 а )

( 27 б )

Приклад 4. Результати випробувань над випадковими величи­нами представлено таблицею 5 (див. перші вісім рядків і шість стовпчиків). Оцінити числові характеристики і функції реґресії складових, коефіцієнт кореляції та кореляційне відношення до .

Таблиця 5. Кореляційна таблиця до прикладу 4

	10	30	50	70
10	9	1			10	12.00
12	4	10	2		16	27.50
14	1	9	6	1	17	38.24
16		3	14	10	27	55.19
18			6	18	24	65.00
20				6	6	70.00
	14	23	28	35
	10.85	13.22	15.71	17.66

Оцінки числових характеристик випадкової величини (див. ліву частину таблиці 6

Таблиця 6. Характеристики складових прикладу 4

№ 1 10 14 140 100 1400 2 30 23 690 900 20700 3 50 28 1400 2500 70000 4 70 35 2450 4900 171500 100 4680 263600

№ 1 10 10 100 100 1000 2 12 16 192 144 2304 3 14 17 238 196 3332 4 16 27 432 256 6912 5 18 24 432 324 7776 6 20 6 120 400 2400 100 1514 23724

Оцінки числових характеристик випадкової величини (див. пра­ву частину таблиці 6)

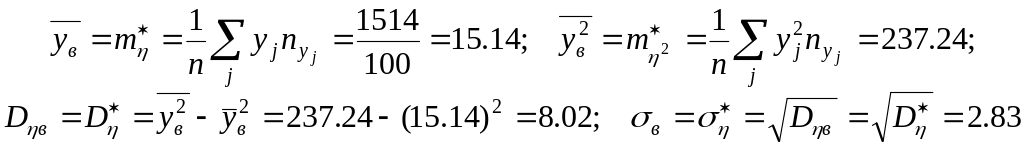
Оцінки значень функції реґресії на , тобто значення умовних середніх , ми дамо за формулами (21 а)

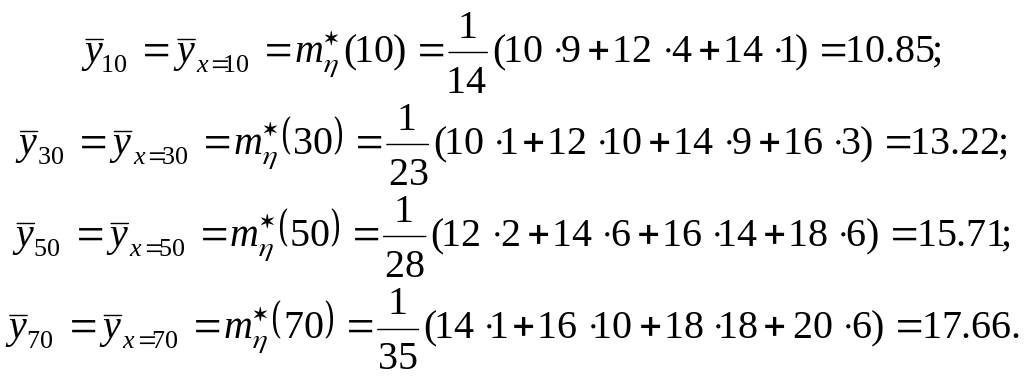
Значення знаходяться в девятому рядку таблиці 5.

Умовні середні , оцінки значень функції реґресії на , знайдемо за формулою (22 а),

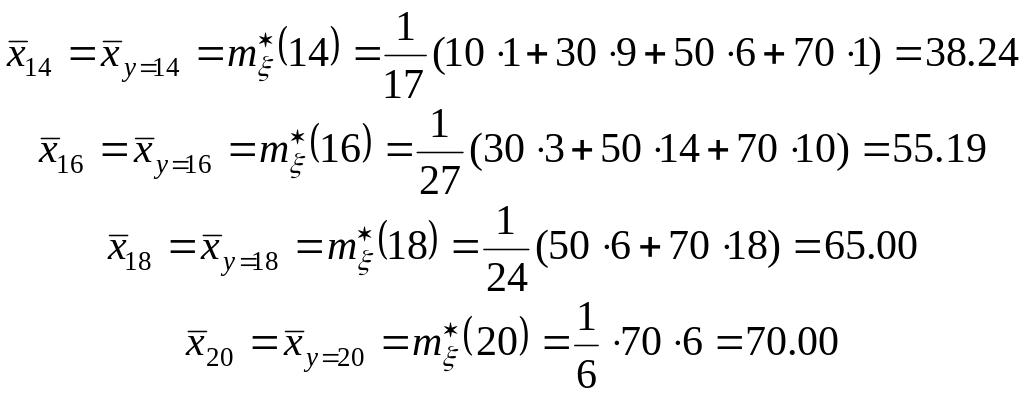
Знайдені оцінки містяться в сьомому стовпчику таблиці 5.

Рис. 3. Статистичі лінії реґресії

На рис. 3 кружечками позначені точки а хрестиками – точки , пунктиром и штрихпунктиром зображені відповідно наближені графіки функцій реґрессії і (ста­тистичні лінії реґресії , ). Близькість статистичних ліній реґресії свідчить про достатьньо тісну кореляційну залежність між випадковими величинами та . Проте чи є ця залежність лінійною чи нелінійною – потрібне дослідження. На рис. 3 лінії реґ-ресії зображені у вигляді прямих, ко­трі перетинаються в точці A, яка мало від-різняється від точки

Кореляційний момент і коефіцієнт кореляції оцінимо за форму­лами (23), (26),

+10∙14∙1+30∙14∙9+50∙14∙6+70∙14∙1+30∙16∙3+50∙16∙14+70∙16∙10+50∙18∙6+70∙18∙18++70∙20∙6) – 46.80∙15.14=

.

Знайдене значення вибіркового (статистичного) коефіцієнта кореляції свідчить про достатньо тісну лінійну залежність між випадковими величинами .

Кореляційне відношення до оцінимо за формулою (27 а). Підкореневий вираз дорівнює

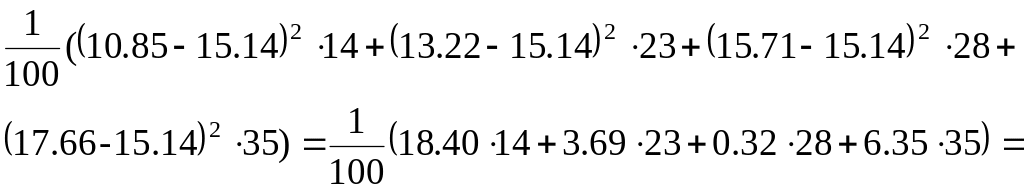
Отже,

Отримали близький до одиниці результат, який свідчить про вельми тіс­ну функціональну залежність між , але ніщо не каже про характер залежності. Статистична ж оцінка коефіцієнта кореляції вказує на те, що ця залежність лінійна.

Переходимо до питання про з”ясування вигляду кореляційної залежності, точніше про визначення параметрів цієї залежності. На підставі основ­ної властивості функцій реґресії питання розв”язується з допомогою методу наймен-ших квадратів (МНК).