5.3.3. Правило Верещагина

Для балок, состоящих из прямолинейных участков с постоянной изгиб-ной жесткостью каждого участка, операция интефирования упрощается. Это упрощение основано на том, что эпюры изгибающих моментов от еди­ничных силовых факторов на прямолинейных участках описываются ли­нейными функциями.

Пусть на прямолинейном участке балки длины / эпюра изгибающего момента от действия заданной системы сил M^f, или грузовая эпюра, опи­сывается функцией fi(,j, т. е. M,f = fi(z), а эпюра изгибающего момента от единичного силового фактора есть линейная функция, т. е.

Рассмотрим интеграл от произведения этих функций:

Таким образом, по правилу (способу) Верещагина операция интегрирования за­меняется умножением площади грузовой эпюры на ординату второй (линейной) эпюры, взятую под центром тяжести первой.

В случае, когда обе функции Мхг и Ми - линейные, операция умножения облада­ет свойством коммунативности, т. е. на результате не сказывается, умножается ли площадь первой эпюры на ординату вто­рой или площадь второй эпюры - на ор­динату первой.

Окончательно математическое выра­жение правила Верещагина записывается следующим образом

Лекции № 6-7-8

Напряженное и деформированное состояние в точке. Понятие о напря­женном состоянии в точке. Напряжения в наклонных сечениях при растя­жении в двух направлениях. Обобщенный закон Гука. Теории прочности.

6. Напряженно-деформационное состояние в точке 6.1. Понятие о главных напряжениях

Основная цель сопротивления материалов - это определение наиболее нагруженной (напряженной) точки анализируемого элемента конструкции (тела) и оценка опасности напряженного состояния в этой точке с позиции прочности. Наиболее нагруженная точка определяется в опасном по за­грузке поперечном сечении по основе анализа эпюр силовых факторов (растягивающей либо сжимающей силы, перерезывающих сил, крутящего момента, изгибающих моментов).

Для характеристики напряженного состояния в выбранной точке (например, т. А, рис. 6.1), через точку проводятся три секущие взаимно перпендикулярные площадки и выделяется элементарный объем в виде

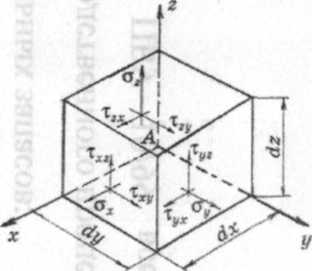
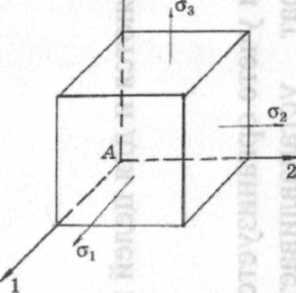
Рне. 7.1. Общее напряженное состояние в т. л и главные напряжения в этой же точке (напряжения указаны на видимых гранях)

прямоугольного параллелепипеда, напряжения на его гранях и рассматри­ваются как напряжения в исследуемой точке.

Таким образом, в общем случае напряженное состояние в точке харак­теризуется совокупностью нормальных (а» о>, oi,) и касательных напряже-

Система сил, приложенных к данному элементарному элементу, должна удовлетворять условиям равновесия. Поэтому из условия равенства нулю суммы проекций всех сил на оси координат следует, что нормальные напряжения на противоположных фанях элемента равны и противополож­но направлены. Условие равенства нулю суммы моментов сил относитель­но осей X, у, Z соблюдается, если выполняется закон парности касательных напряжений, т.е. когда на двух взаимно перпендикулярных площадках со­ставляющие касательных напряжений, перпендикулярные общему ребру, равны и направлены обе либо к ребру, либо от него:

На невидимых фанях элемента действуют такие же напряжения, как на видимых гранях, но противоположно направленные.

В теории упругости доказывается, что около выделенной т. А паралле­лепипед можно повернуть таким образом, что на гранях (площадках) будут действовать только нормальные напряжения. Такое положение фаней око­ло выбранной точки называется главными площадками (рис. 6.1). Нор­мальные напряжения, действующие на главных площадках называются главными напря.жениями, а их направления - главными направлениями. Принято с учетом знака главных напряжений обозначать большее из них Gi, среднее - аг и меньшее - Оз или:

(Т1>сг2>аз. (6.1)

Совокупность трех главных напряжений является обобщенной характе­ристикой трехосного состояния в данной точке (элемента конструкции, де­тали). По их совокупности и делается вывод о прочности.

Экспериментально доказано, что влияние среднего по величине (ог) главного напряжения на прочности не превышает 10... 12%, поэтому для инженерной практики наиболее важен случай двухосного напряженного состояния (плоского), когда отличны от нуля наибольшее (oi) и наимень­шее (оз) напряжения. К этому случаю сводится совместное действие на брус растяжения и кручения, кручения и изгиба.

Рассмотрим аналитическое исследование двухосного напряженного со­стояния.

6.2. Определение напряжений на площадке произвольного положения Пусть у выбранной т. А тела наблюдается плоское напряженное состоя­ние (рис. 7.2).

Выделим в окрестности точки призму abca'b'c', на фани bb'cc' которой действует нормальное напряжение (т„ и касательное г„ (и - нормаль к этой грани, / - касательная). Рассмотрим равновесие данной призмы, приняв площадь наклоненной грани bb'cc' за А. Тогда площадь грани aa'bb', пер­пендикулярной оси X - Acosa, а грани аа'сс', перпендикулярной оси у -Asina. На грани aa'bb', относительно которой на угол а повернута площад-

Сумма проекций всех сил на нормаль п:

Формула для определения по­ложения главных площадок, т.е. площадок, на ко­торых касательные напряжения равны нулю, сле­дует из выраже­ния (6.3) при =0:

Два угла «о и а +90° определя­ют по этой фор­муле положение главных площа­док около анали­зируемой точки А. Подстановкой найденных значе­ний углов Оо и ао+90° в выраже-

Определим из (7.4) напряжение на площадке с углом а + 90°:

аа+90° = Gx sin2a + ay cos2a + zsin2a. Сложив выражения для Оа и <У(ао+90), получим

ffn + Оа^т- = (Тх (sin2a +cos2a) + Оу (cos2a + sm2a)= Ох + ay. Таким образом, сумма нормальных напряжений на любых двух взаимно перпендикулярных площадках есть величина постоянная и равная

мальных напряжении обычно пользуются для проверки правильности их вычислений. Для определе­ния положения площадок, на которых касательные напряжения имеют наи­большее значение рассмот-

Рнс. 7.3. Расчетная схема оценки максимальных рим главный элементарный каеатв.чьных напряжений параллелепипед около т. А и в нем проведем площадку под углом а к главной площадке с напряжением О] (рис. 6.3) и параллель­ную второму главному направлению.

Условие равновесия призмы (рис. 6.3) сводится к равенству нулю суммы проекций всех сил на оси п и t (нормаль и касательную к проведенной пло­щадке):

Из выражения (6.6) следует, что наибольших значений касательные напряжения достигают на площадках, составляющих с направлениями главных площадок углы а = ±45° на этих площадках:

Необходимо отметить, что на площадках наибольших касательных напряжений действуют также и нормальные напряжения, равные полусум­ме главных напряжений. Из (6.6) следует: