3.3.5. Устойчивость и сходимость мер

Когда динамическая система обладает хаотическим поведением, у нее наряду с аттрактором может существовать бесконечное число неустойчивых периодических циклов. Каждый из этих неустойчивых циклов является носителем своей эргодической меры, так что эргодических мер оказывается бесконечно много. С другой стороны, очевидно, что не все меры существенны, и наблюдаемому в эксперименте (вычислительном или физическом) поведению отвечает только одна из них. Такие меры и получили название физических мер. Они связаны с определенными свойствами устойчивости. Как устойчивое инвариантное множество обладает окрестностью, все точки которого стремятся к нему при , так и малые возмущения устойчивой меры должны “затухать” с ростом . Очевидно, что носителем такой устойчивой меры должно быть притягивающее множество, аттрактор.

Существует два способа введения понятия устойчивости меры. Первый связан с добавлением бесконечно малого случайного шума, амплитуда которого стремится к нулю.

Другой способ связан с исследованием сходимости последовательности мер под действием оператора Перрона–Фробениуса. На этом пути возникают трудности. Первая трудность определяется необходимостью исследования спектра оператора Перрона–Фробениуса, а вторая – с тем, что пределом последовательности непрерывных мер часто бывает сингулярная мера. В этом случае уравнение Перрона–Фробениуса следует понимать в обобщенном смысле и использовать интегрирование по мере, а не по плотности вероятности.

Скорость сходимости мер зависит от их гладкости. Например, непрерывные распределения “хорошо” сходятся к инвариантным мерам. Распределение в виде ‑функции сходиться вообще не будет, оставаясь таким всегда.

3.4. Эргодичность и перемешивание

Эргодичность часто определяют как совпадение средних значений по времени и средних по пространству. Понятие эргодичности было введено Больцманом в связи с основаниями статистической механики. Однако и многие динамические системы с фазовым пространством небольшой размерности, траектории которых равномерно и плотно заполняют фазовое многообразие, обладают свойством эргодичности.

Эргодичность – необходимое, но не достаточное условие хаотичности движения динамической системы. Если спустя некоторое время начальная область распределяется по всей гиперповерхности так, что ее “кусочки” можно обнаружить в любой ее части, то система обладает перемешиванием. Свойство перемешивания может служить критерием хаотичности движения.

3.4.1. Эргодичность

Рассмотрим консервативную динамическую систему, для которой имеет место сохранение с течением времени фазового объема. Пусть  – ее фазовые переменные и  – интегрируемая, зависящая от фазовых координат функция.

Средним по времени значением функции называется величина

. (3.24)

Обозначив через  – фазовый поток, для которого справедливо , получим

.

Т. е. среднее значение функции по времени зависит от начального состояния. Однако, для почти всех (кроме множества меры нуль) начальных условий функция является инвариантной (не меняется при перенесении начального условия вдоль траектории). Пусть движение системы в фазовом пространстве происходит в ограниченной области с объемом .

Фазовым средним значением функции называется величина

. (3.25)

Здесь .

Движение системы называется эргодическим, а сама система – эргодической, если для любой интегрируемой функции и для любых начальных условий имеет место равенство временных (3.24) и фазовых (3.25) средних значений.

. (3.26)

Таким образом, для эргодической системы среднее по времени (3.24) не зависит от начальной точки траектории.

Рассмотрим область , и пусть  – характеристическая функция множества :

. (3.27)

Функция (3.27) интегрируема

.

Фазовое среднее характеристической функции (3.27) есть “относительный объем” области . Если движение динамической системы обладает свойством эргодичности, то относительное время, проведенное фазовой траекторией внутри любой области , равно относительному объему этой области и не зависит от выбора начальных условий. Иными словами, фазовая кривая эргодической системы равномерно и плотно заполняет весь объем области .

Относительный объем или относительная площадь некоторой области представляет собой меру этой области. Используя понятие меры, определение эргодичности (3.26) можно записать как

,

где интегрирование ведется по всей доступной области фазового пространства. При этом

.

Примером эргодического поведения может служить квазипериодическое движение гамильтоновой системы, состоящей из двух гармонических осцилляторов с иррациональным отношением частот.

Действие фазового потока на малую область , принадлежащую поверхности двумерного тора представлено на рис. 3.5.

Характерной особенностью эргодического движения Гамильтоновой системы является сохранение не только объема, но и формы исходной области. Фазовая кривая плотно покрывает поверхность тора.

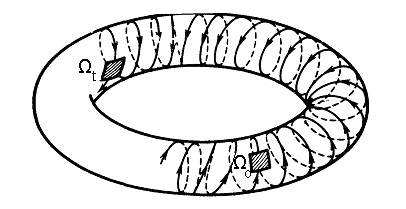
Рис. 3.5. Эргодическое движение на двумерном инвариантном торе