3.2. Характеристические показатели ляпунова

Одна из особенностей нерегулярных режимов – неустойчивость траекторий, принадлежащих хаотическому или странному аттрактору. Количественной мерой этой неустойчивости являются характеристические показатели, введенные первоначально Ляпуновым для исследования поведения одной траектории. Характеристические показатели Ляпунова предлагались как обобщение собственных значений постоянных матриц на случай зависящих от времени матриц, которые возникают при исследовании устойчивости нелинейных динамических систем. Характеристические показатели являются усредненными аналогами собственных значений.

3.2.1. Непрерывные динамические системы

Пусть задана автономная динамическая система

, (3.1)

где  ‑ начальные данные. Определим изменение траектория при бесконечно малом приращении начальных данных , рассматривая бесконечно близкую траекторию . Решение системы (3.1) дифференцируемо по начальным данным для конечных значений времени , поэтому

,

где  – матрица производных от решения по начальным данным.

Для линейных систем матрица совпадает с нормированной фундаментальной матрицей. Для нелинейной системы по заданному начальному возмущению можно найти , решая соответствующую линейную систему

, (3.2)

где  – матрица Якоби.

В силу линейности уравнения (3.2) амплитуда решения несущественна. Важен «коэффициент приращения» решения за время , поэтому от бесконечно малых величин можно перейти к конечным значениям , считая . Бесконечно малая амплитуда , входящая, как в правую, так и левую части уравнений, сокращается. Тогда исследование устойчивости системы (3.1) сводится к исследованию устойчивости линейной системы вида

. (3.3)

Начальное возмущение определяет направление, в котором мы выбираем бесконечно близкую траекторию в точке . Векторы и принадлежат к разным пространствам: принадлежит фазовому пространству динамической системы, а  – касательному пространству в точке (рис. 3.1).

Рис. 3.1. Касательное пространство в точке

Решение системы (3.3) удобно выразить через нормированную фундаментальную матрицу , которая удовлетворяет тем же самым дифференциальным уравнениям

.

Тогда решение системы (3.3) можно представить в виде . Для одних направлений вектора (выбранного вектора начальных условий) близкие траектории будут экспоненциально удаляться. Для других векторов траектории будут экспоненциально сближаться, для третьих – расстояние между траекториями остается постоянным или меняется медленнее, чем экспоненциально. Для неподвижной точки имеем , и эти случаи соответствуют собственным значениям с вещественными частями: . Здесь  – собственные значения матрицы .

А.М. Ляпунов для описания поведения решений динамической системы ввел характеристический показатель функции .

Определение 3.1. Характеристическим показателем функции называется число (или символ ), определенное как

. (3.4)

Характеристический показатель определяет изменение модуля функции по шкале показательных функций . Для этих функций характеристический показатель равен . Для произвольных функций справедливо тождество

,

которое и поясняет определение 3.1.

Определим значения характеристического показателя в случае неподвижной точки системы (3.1) . Пусть все собственные значения матрицы линеаризованной системы (3.3) вещественны, различны и пронумерованы в порядке убывания: . Обозначим соответствующие им собственные векторы , , . Собственные векторы образуют базис в касательном пространстве в точке . Любое решение системы (3.3) можно представить как линейную комбинацию базисных решений , отвечающих начальным данным . Если , то общее решение уравнения (3.3) имеет вид

. (3.5)

Пусть  – номер, при котором , . Тогда решение системы (3.3) будет определяться соотношением

,

и характеристический показатель Ляпунова (3.4) равен

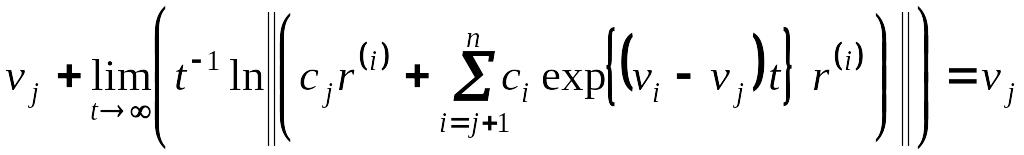= . (3.6)

Соотношение (3.6) имеет следующую геометрическую интерпретацию. Каждый собственный вектор задает инвариантное направление в касательном пространстве векторов . Если вектор начального смещения направлен вдоль одного из векторов , тогда остается параллельным ему. С течением времени расстояние между траекториями возрастает или убывает по экспоненциальному закону: . При таком выборе вектора начального смещения имеем .

В общем случае вектор начального смещения имеет составляющие вдоль нескольких или всех векторов . При больших моментах времени изменение расстояния между двумя траекториями будет определяться слагаемым с наибольшим показателем экспоненты в разложении (3.5) вектора . В зависимости от того, какие собственные векторы присутствуют в разложении вектора начального смещения , доминирующая экспонента будет различна.

Однако при достаточно больших моментах времени расстояние пропорционально какой-либо из экспонент . Следовательно, функция может принимать значения, равные только , и при повороте вектора могут происходить только скачкообразные изменения функции . Таким образом, характеристический показатель может принимать только различных значений в зависимости от начальных данных.

У матрицы могут быть кратные и комплексные собственные значения. В этом случае вещественных векторов может не быть, а будут минимальные инвариантные подпространства (для любого ) размерности , , при этом .

Среди всего набора характеристических показателей Ляпунова наиболее важен наибольший (старший) показатель . Покажем, что при произвольном выборе начального смещения предел (3.4) дает максимальный характеристический показатель Ляпунова. Произвольно взятый вектор будет иметь проекции на все векторы , в том числе и на тот из них, который отвечает максимальному значению собственного числа . При больших временах экспонента с этим значением в разложении (3.5) будет доминировать, а поэтому предел в (3.6) будет давать значение .

Чтобы получить меньшее значение характеристического показателя , необходим специальный выбор начальных данных. Простейший случай соответствует выбору одномерных инвариантных подпространств и

.

Здесь  ‑ линейная оболочка системы векторов, перечисленных выше в фигурных скобках.

Кроме обычных показателей , характеризующих одно решение (растяжение или сжатие в одном направлении), используют показатели Ляпунова порядка , которые определяют изменение ‑мерных фазовых объемов ( ). Пусть  – линейно независимые решения, а  – объем образуемого ими ‑мерного параллелепипеда, который равен

.

Здесь  – скалярное произведение векторов.

Определение 3.2. Характеристическим показателем порядка называется число, определенное как

. (3.7)

Подобно тому, как типичным значением характеристического показателя является , типичным значением характеристического показателя ‑го порядка является .

Среди всех выделяется показатель ‑го порядка. Любой набор линейно независимых решений образует фундаментальную матрицу . Ее определитель называется определителем Вронского . С его помощью фазовый объем можно записать в виде

= .

Для уравнения (3.3) справедливо: или . Отсюда следует, что характеристический показатель  ‑ го порядка равен

.

Если существует точный предел, тогда

.

Здесь  – среднее по времени значение следа матрицы .

В последнее соотношение для характеристического показателя вектор не входит, поэтому этот показатель является характеристикой всей динамической системы, а не ее отдельно взятой траектории. В зависимости от значения характеристического показателя ‑го порядка динамические системы подразделяются на консервативные, сохраняющие ‑мерные фазовые объемы ( ), и диссипативные ( ), фазовые объемы которых сжимаются.

Набор показателей Ляпунова линеаризованной системы (3.3) характеризует устойчивость траектории нелинейной системы (3.1). Если , то траектория асимптотически устойчива; если  ­ неустойчива. Набор характеристических показателей упорядоченных по убыванию называют ляпуновским спектром нелинейной динамической системы (3.1).

Пример. Для системы Лоренца

имеем

,

, .

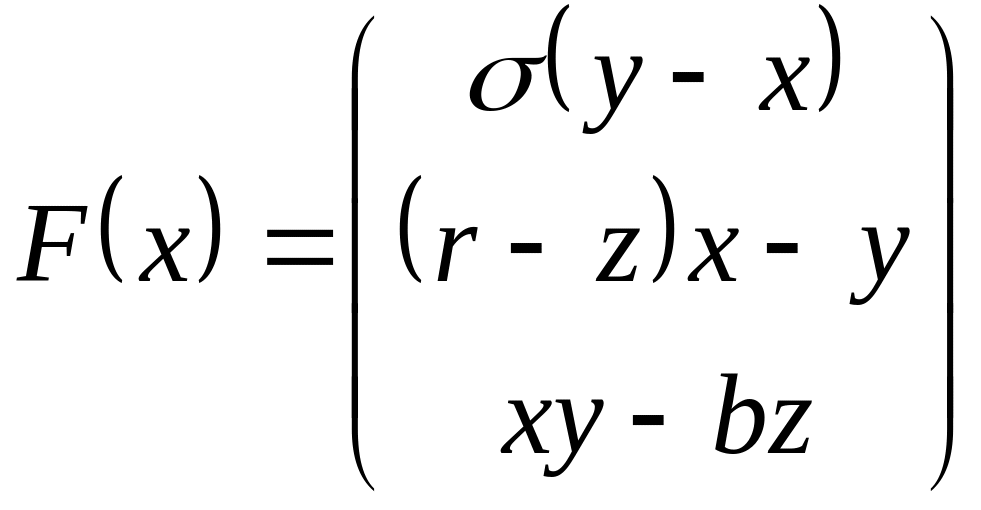Так как след матрицы не зависит от траектории и от времени, он и будет средним значением. Для аттрактора системы Лоренца характеристический показатель (3.7) третьего порядка равен .