7 Применение теории пластичности в омд

7.1 Постановка задач при расчетах процессов омд

В общем случае требуется:

По заданной исходной форме заготовки и инструмента, при известных механических свойствах металла заготовки и условиях трения на поверхностях контакта металла с инструментом, известном распределении температур в заготовке и условиях ее остывания, при заданном перемещении и(или) скорости инструмента относительно заготовки определить:

Задача 1: усилия и моменты, необходимые для осуществления за- данной деформации;

Задача 2: форму тела после деформации, если у заготовки есть свободные поверхности;

Задача 3: распределение напряжений и деформаций по всему телу в процессе деформирования.

Задача 1 является первой задачей, с которой сталкивается технолог при разработке любого процесса деформирования. Будет ли способна данная машина для ОМД осуществить заданную деформацию? Для этого нужно знать нагрузки, которые возникнут при работе. Каковы должны быть энергосиловые возможности машины, если стоит задача ее выбора? Для этого также нужно знать усилия и моменты, которые нужно преодолеть для деформирования. Легко видеть, что первая задача сводится к определению статических граничных условий данного процесса деформации. Действительно, например при прошивке заготовки на прессе усилие прошивки Р будет поверхностным интегралом от распределения нормальных напряжений по торцу пуан-

сона (рис.7.1).

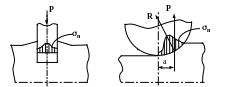
Прошивка на прессе Прокатка

Рисунок 7.1 − Первая задача ОМД

При прокатке таким же интегралом будет равнодействующая усилия прокатки R. Ее вертикальная составляющая Р вызывает поломку валков и поэтому является огрнаничивающим фактором этого процесса, а произведение Р на величину плеча момента а является моментом прокатки, который должен преодолевать двигатель прокатной клети.

Ранее уже указывалось (см.п.5.5), что определение граничных условий по полю внутри тела является т.н. «обратной задачей». Однако в данном случае неизвестно и поле напряжений в деформируемом теле, поэтому первая задача одновременно является и самой трудной.

Вторая задача возникает в тех случаях, когда при деформировании у заготовки есть т.н. «свободные поверхности», т.е. поверхности, на которых металл не контактирует с инструментом. Здесь у металла имеется возможность перемещаться в направлениях, наиболее выгодных в энергетическом отношении и поэтому форму тела после деформации предсказать без расчета нельзя. Между тем во многих случаях ее нужно знать для построения технологического процесса таким образом, чтобы минимизировать отходы металла. Например, при прокатке толстых листов форма раскатов в плане получается далекой от требуе-

мой прямоугольной (рис.7.2).

Рисунок 7.2 − Форма толстолистового раската

Вырезание из раскатов листов сопровождается появлением обрези, ухудшающей технико-экономические показатели производства.

Третья задача как самостоятельная технологическая проблема возникает сравнительно редко. Например, при прокатке на обжимных станах слитков по оси раската возникают растягивающие напряжения, которые могут приводить к появлению разрывов, т.е. к браку. Расчет поля напряжений в металле позволяет так строить процесс, чтобы эти напряжения не превышали допустимых. Однако без определения полей напряжений и деформаций в металле невозможно решить первые две задачи. Поэтому теоретическое значение третьей задачи велико.

В связи со сложностью задач пластического деформирования при расчетах процессов ОМД часто прибегают к различным упрощениям. Например, при расчетах горячей ОМД процессы считают изотермическими, т.е. не учитывается тепловой эффект деформации, изменение температурного поля в металле при его остывании в процессе обработки. Упрочнение учитывается усредненно – сопротивление деформации считается одинаковым во всех точках тела и его значение берется средним от значений в начале и в конце деформирования.