
- •8 Приложения. Элементы векторной и тензорной алгебры
- •1.1 Задачи курса «Механика сплошных сред»
- •1.2 Предмет механики сплошной среды
- •1.3 Методы механики сплошной среды
- •1.4 Основные принципы механики сплошной среды
- •1.5 Элементарный объем
- •1.6 Переменные Лагранжа и Эйлера
- •1.7 Движение и равновесие сплошной среды
- •2 Статика сплошной среды
- •2.1 Напряжение в точке
- •2.2 Напряженное состояние в точке
- •2.3 Соотношения Коши и компоненты напряженного
- •2.4 Тензор напряжений
- •2.5 Доказательство тензорности напряженного состояния*
- •2.6 Условия симметричности тензора напряжений
- •2.7 Доказательство равенства парных касательных
- •2.8 Общий случай напряженного состояния*
- •2.9 Главные напряжения
- •2.10 Нормальные и касательные напряжения
- •2.11 Максимальные касательные напряжения
- •2.12 Шаровой тензор и девиатор напряжений
- •2.13 Изображение напряженного состояния в точке
- •2.14 Октаэдрические напряжения и интенсивности
- •2.15 Уравнения равновесия
- •2.16 Уравнения равновесия в недекартовых системах
- •2.17 Уравнения равновесия в общем случае *
- •2.18 Краевая задача статики сплошной среды
- •3 Кинематика сплошной среды
- •3.2 Абсолютная и относительная деформация
- •3.3 Поле относительных смещений
- •3.4 Составляющие движения сплошной среды
- •3.5 Тензор малых деформаций
- •3.6 Геометрический смысл компонент тензора малых
- •3.7 Тензоры конечных деформаций
- •3.8 Общий случай малых деформаций *
- •3.9 Анализ деформированного состояния в точке
- •3.10 Инварианты тензора малых деформаций
- •3.11 Главные деформации
- •3.12 Максимальные угловые деформации
- •3.13 Октаэдрические деформации и интенсивности
- •3.14 Условия совместности деформаций
- •3.15 Определение перемещений по деформациям*
- •3.16 Поле скоростей
- •3.17 Первая теорема Гельмгольца
- •3.18 Тензор скоростей деформаций
- •3.19 Свойства тензора скоростей деформаций
- •3.20 Вторая теорема Гельмгольца*
- •4 Элементы термодинамики сплошных сред
- •4.1 Термодинамические системы и параметры состояния
- •4.2 Законы сохранения
- •4.3 Теоремы э. Нётер и свойства симметрии
- •4.4 Закон сохранения массы и уравнение неразрывности
- •4.5 Вывод уравнения неразрывности*
- •4.6 Теорема «живых сил»
- •4.7 Первое начало термодинамики
- •4.8 Уравнение теплопроводности
- •5 Основы теории упругости
- •5.1 Предмет теории упругости
- •5.2 Обобщенный закон Гука
- •5.3 Упругое изменение объема и формы
- •5.4 Потенциальная энергия упругого деформирования
- •5.5 Постановка задач в теории упругости
- •5.6 Решение задач теории упругости в перемещениях
- •5.7 Решения задач теории упругости в напряжениях
- •5.8 Плоское напряженное состояние*
- •5.9 Плоское деформированное состояние*
- •5.10 Плоская задача в моментной теории упругости *
- •5.11 Функция напряжений*
- •5.12 Способы решения задач теории упругости*
- •6 Основы теории пластичности
- •6.1 Предмет теории пластичности
- •6.2 Переход в пластическое состояние при растяжении
- •6.3 Условия пластичности
- •6.6 Экспериментальная проверка условий
- •6.7 Теории пластичности
- •6.8 Теория пластического течения
- •6.10 Постулат Друкера и ассоциированный закон
- •6.11 Области применимости различных теорий пластичности
- •6.12 Экстремальные принципы пластического
- •7 Применение теории пластичности в омд
- •7.1 Постановка задач при расчетах процессов омд
- •7.2 Математический аппарат и краевые условия при омд
- •7.3 Способы решения задач теории пластичности
- •1.Численные методы;
- •2.Прямые методы получения решений на основе экстремальных принципов мсс;
- •3.Уменьшения числа независимых переменных и искомых функций.
- •7.4 Частные виды напряженно-деформированных
- •1. Толщина пластины значительно меньше остальных размеров;
- •2. Деформирующие усилия приложены в срединной плоскости пластины.
- •7.5 Особенности плоского деформированного состояния
- •7.6 Осесимметричное деформированное состояние
- •7.7 Метод линий скольжения
- •7.8. Свойства линий скольжения
- •7.9 Простые сетки линий скольжения
- •7.10 Статические граничные условия в млс
- •7.11 Задача о внедрении штампа в полупространство
- •7.12 Основные краевые задачи в млс*
- •7.13 Определение поля скоростей в млс*
- •7.14 Полные решения задач плоской деформации
- •Пластичности в омд”
- •8. Приложения. Элементы векторной и тензорной алгебры и анализа
- •8.1 Скаляры и векторы
- •8.2 Векторный базис
- •8.3 Сложение и умножение векторов
- •8.4 Тензоры 2-го ранга
- •8.5 Преобразование компонент тензора
- •8.6 Сложение и умножение тензоров
- •8.7 Симметрирование и альтернирование тензоров
- •8.8 Умножение тензора на вектор
- •8.9 Главные оси тензора
- •8.10 Определение величины и направления главных компонент тензора
- •8.12 Поверхности уровня и градиент скалярного поля
- •8.13 Векторное поле и векторные линии
- •8.14 Поток и дивергенция векторного поля
- •Теорема Остроградского–Гаусса:
- •8.15 Циркуляция и ротор векторного поля
- •8.16 Оператор («набла»)
- •8.17 Дифференциальные операции 2-го порядка
- •8.18 Потенциальные векторные поля
- •8.20 Гармонические векторные поля
- •8.21 Основная теорема векторного анализа
- •8.22 Производная и градиент векторного поля
- •8.23 Поток тензорного поля
- •8.24 Дивергенция тензорного поля
- •8.25 Производная тензорного поля по направлению
- •Предметный указатель
- •Перечень ссылок
6.12 Экстремальные принципы пластического
деформирования*
В теории пластичности большое значение имеют теоремы об экстремальных свойствах решений пластических задач, поскольку они
дают возможность получать решения без представющего значительные трудности интегрирования систем нелинейных дифференциальных уравнений. Из этих теорем следуют т.н. экстремальные принципы, особенно важное значение имеющие для жестко-пластических сред. Ранее уже указывалось на неединственность решения жестко-пластических задач и возникающей из-за этого проблемы выбора решения. Экстремальные принципы дают критерий выбора.
В деформационной теории экстремальные теоремы являются обобщением соответствующих теорем минимума для упругих сред (теоремы минимума полной энергии системы и теоремы Кастилиано). Они применяются для приближенного решения различных задач прямыми методами, в основном методом Ритца.
Экстремальные
принципы для упруго-пластических сред,
как при наличии упрочнения, так и для
идеальной пластичности, при использовании
теории течения определяют экстремальные
свойства приращений (или скоростей)
смещений
![]() и
приращений напряжений, соответствующих
малым приращениям внешних сил или
перемещений. Но эти принципы в связи с
их локальностью, следующей из
дифференциального характера уравнений
Прандтля-Рёйсса, труднее использовать
для получения решений.
и
приращений напряжений, соответствующих
малым приращениям внешних сил или
перемещений. Но эти принципы в связи с
их локальностью, следующей из
дифференциального характера уравнений
Прандтля-Рёйсса, труднее использовать
для получения решений.
На экстремальных принципах для жестко-пластических сред основаны методы верхней и нижней оценок, ныне применяющиеся в инженерной практике, поэтому остановимся на них подробнее.
Рассмотрим
тело произвольной формы объемом W,
ограниченное поверхностью F
= Fσ+
Fv
(рис.6.22). На части поверхности тела Fσ
задан вектор полного напряжения
с
компонентами
![]()
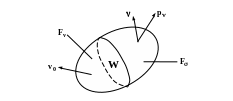
Рисунок 6.22 − К выводу основного энергетического уравнения
На
остальной части - вектор скорости течения
![]() с
компонентами
с
компонентами
![]() Объемные
силы отсутствуют. В теле под воздействием
внешних нагрузок
возникло непрерывное поле напряжений,
удовлетворяющих уравнениям равновесия
и статическим граничным условиям на Fσ
согласно соотношений Коши. Во всем теле
имеется также непрерывное поле скоростей,
удовлетворяющее кинематическим граничным
условиям на Fv.
В остальном поля напряжений и скоростей
произвольны и, в общем случае, не связаны
друг с другом. Форма тела после деформации
мало отличается от начальной или же
характеризует известное текущее
состояние.
Объемные
силы отсутствуют. В теле под воздействием
внешних нагрузок
возникло непрерывное поле напряжений,
удовлетворяющих уравнениям равновесия
и статическим граничным условиям на Fσ
согласно соотношений Коши. Во всем теле
имеется также непрерывное поле скоростей,
удовлетворяющее кинематическим граничным
условиям на Fv.
В остальном поля напряжений и скоростей
произвольны и, в общем случае, не связаны
друг с другом. Форма тела после деформации
мало отличается от начальной или же
характеризует известное текущее
состояние.
При выполнении этих условий для всякой сплошной среды справедливо основное энергетическое уравнение:
![]() ,
(6.26)
,
(6.26)
где первый интеграл характеризует диссипацию (рассеивание) энергии
при пластическом деформировании, а второй – мощность поверхнос-
тных сил, вызвавших деформацию.
Уравнение (6.26) справедливо и для тел, содержащих жесткие (недеформированные) области. Можно доказать (см., например, [28]), что наличие разрывов в напряжениях не сказывается на форме уравнения (6.26). Разрывы в скоростях требуют его некоторого обобщения.
В
общем случае разрывы возможны только
в касательной составляющей скорости,
лежащей в касательной плоскости к
поверхности разрыва
![]() (рис.6.23).
(рис.6.23).
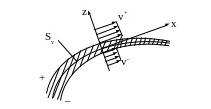
Рисунок 6.23 − Разрыв скорости
В противном случае тело будет терять сплошность. Поверхность разрыва рассматривается как предельное положение тонкого слоя с непрерывным и быстрым изменением касательной составляющей скорости Vx от V+ до V-. Касательное напряжение на поверхности разрыва Sv обозначим τ. Тогда основное энергетическое уравнение примет вид:
![]() (6.27)
(6.27)
где [v] – скачок скорости от V+ до V-,
SΣ – сумма всех поверхностей разрыва скорости.
Уравнение (6.27) справедливо для любых сред, находящихся в равновесии. Скорости и напряжения, входящие в него, в общем случае не связаны друг с другом. Если среда подчиняется уравнениям Сен-Венана-Леви-Мизеса, то поверхность разрыва является поверхностью τmax (поверхностью скольжения).
Наряду с действительными полями напряжений и скоростей можно рассматривать виртуальные (возможные или допустимые) поля. Виртуальным перемещением в аналитической механике называется перемещение, которое допускают наложенные на систему связи. Аналогично вводятся определения:
Поле напряжений является статически допустимым, если оно удовлетворяет уравнениям равновесия и статическим граничным условиям.
В случае идеальной пластичности оно должно удовлетворять и какому-либо условию пластичности.
Поле скоростей является кинематически допустимым, если оно удовлетворяет условию несжимаемости (4.3) и кинематическим граничным условиям.
Известна теорема о минимальных свойствах действительного поля скоростей [3,25,28,36]. Сопоставляя баланс мощности внешних и внутренних сил с учетом разрывов скорости по уравнению (6.27) для действительного и кинематически допустимого полей скоростей при действительном поле напряжений приходят к выводу:
Полная мощность достигает абсолютного минимума для действительного поля скоростей.
Отсюда делается вывод, что если при решении задачи использова-
но не действительное, а только кинематически допустимое поле ско-ростей, то найденная по этому решению нагрузка будет больше дейст-вительной.
Нагрузка, найденная по кинематически допустимому полю скоростей, и поэтому заведомо превышающая действительную, называется верхней оценкой нагрузки.
На этом основан метод верхней оценки (МВО), в котором вместо неизвестного сложного поля скоростей используют довольно простые кинематические допустимые поля скоростей, по которым находится нагрузка. Считается, что эта нагрузка во всех случаях будет больше действительной и поэтому она является верхней оценкой. Более подробно с МВО можно ознакомится по [35].
Известна также теорема о максимальных свойствах действительного поля напряжений. Сопоставляя статически допустимые поля напряжений с действительным при действительном поле скоростей по основному энергетическому уравнению (6.27) с учетом разрывов в ско-ростях и напряжениях, приходят к выводу:
Мощность действительных поверхностных сил на заданных скоростях больше мощности, развиваемой поверхностными силами, соответствующими любому другому статически допустимому полю напряжений.
Отсюда следует вывод: если при решении использовано не действительное, а только статически допустимое поле напряжений, то найденная по нему нагрузка будет заведомо меньше действительной.
Нагрузка, найденная по статически допустимому полю напряжений, и поэтому заведомо меньшая действительной, называется нижней границей нагрузки.
На этом положении основан метод нижней оценки (МНО), по которому строится статически допустимое поле напряжений, соответст
вующее которому поле скоростей не будет кинематически допусти-мым. Найденная по этому решению нагрузка считается во всех случаях нижней оценкой.
МНО менее популярен, чем МВО, поскольку получение статически допустимых полей напряжений является значительно более трудной задачей, чем построение кинематически допустимых полей скоростей.
Путем согласования поля скоростей, соответствующего статически допустимому полю напряжений, с кинематически допустимым полем скоростей, осуществляется сближение верхней и нижней оценок. Считается, что они совпадут при действительных полях напряжений и скоростей.
Доказательства кинематической и статической теорем можно най-ти в учебниках [3,4,28,36] или в монографиях [25,35].
Контрольные вопросы к гл. "Основы теории пластичности"
1. Что изучает теория пластичности?
2. Что называется пределом текучести?
3. Что называется истинным сопротивлением деформации?
4. Что понимается под условиями пластичности?
5. Что называется поверхностью и контуром текучести?
6. Какими свойствами обладает контур текучнсти?
7. Сформулировать условие пластичности Треска-Сен-Венана.
8. Как выглядят уравнения условия Треска-Сен-Венана в общем
случае?
9. Какова геометрическая интерпретация условия Треска-Сен-
Венана?
10.Каковы недостатки условия Треска-Сен-Венана?
11.Почему условие Треска-Сен-Венана используется в ОМД?
12.Дать энергетическую формулировку условия пластичности
Губера-Мизеса.
13.Какова математическая формулировка условия Губера-Мизеса?
14.Выразить условие Губера-Мизеса через интенсивность напряжений.
15.Какова геометрическая интерпретация условия Губера-Мизеса?
16.Дать определение условию Губера-Мизеса как условию постоянства
октаэдрических напряжений.
17.Каковы достоинства и недостатки условия Губера-Мизеса?
18.Какие задачи решают теории пластичности (в узком смысле этого
термина)?
19.Какие модели сплошных сред используются в ОМД?
20.Каковы основные положения теории пластического течения?
21.Что называется параметром Удквиста?
22.Что описывают уравнения Прандтля-Рёйсса?
23.Когда применими уравнения Сен-Венана-Леви-Мизеса?
24.Каковы основные положения деформационной теории?
25.Как диаграмму растяжения превратить в диаграмму деформирова-
ния?
26.Почему применение деформационной теории в общем случае при-
водит к неудовлетворительным результатам?
27.Какое нагружение называется простым?
28.Сформулировать теорему о простом нагружении.
29.Каковы области применимости различных теорий пластичности?
30.Какое поле напряжений является статически допустимым?
31.Какое поле скоростей считается кинематически допустимым?
32.Что доказывает теорема о минимальных свойствах действительного поля скоростей?
33.Что доказывает теорема о максимальных свойствах действительного поля напряжений?
34.Какая нагрузка при деформировании называется верхней оценкой? нижней оценкой?
