6.10 Постулат Друкера и ассоциированный закон
течения*
Процессы
пластического деформирования таких
поликристаллическиих тел, как металлы,
особенно в горячем состоянии, весьма
сложны. Ранее указывалось, что в связи
с этим еще не создана теория пластичности,
которая бы описывала их исчерпывающим
образом. Как деформационная теория,
так и теория течения являются приближенными
моделями этих процессов. Поэтому
возникает вопрос: каковы границы
применимости этих моделей? Чтобы на
него ответить, нужно несколько глубже
вникнуть в основания, на которых построены
указанные теории. Этими основаниями
являются постулат Друкера и ассоциированный
закон течения совместно с условием
непрерывности перехода пластических
деформаций в упругие при непрерывном
изменении направления вектора догружения
.
Известно, что по своим реологическим свойствам металлы не одинаковы. Все холоднодеформируемые металлы и сплавы и начальные стадии их горячего деформирования имеют монотонно возрас-
таюющие
диаграммы деформирования (рис.6.16).
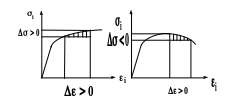
Рисунок 6.16 Рисунок 6.17
Все углеродистые и большинство легированных сталей при температурах горячего деформирования имеют один максимум на диаграмме деформирования (рис.6.17). Цветные металлы и сплавы характерны еще большей реологической сложностью, т.к. имеют два и более экстремума [29].
В
случае рис.6.16 дополнительное нагружение
вызывает дополнительную деформацию
и работа добавочных напряже-ний на
дополнительных деформациях
будет
положительной:
.
В случае рис.6.17 кривая имеет нисходящую
ветвь и де-формация продолжается при
убывающей интенсивности напряжений в
результате разупрочнения металла. На
нисходящей ветви дополнительные
напряжения
выполняют отрицательную работу на
дополнительных деформациях:
<
0, что
уменьшает
всю работу.
Рассмотрим, следуя [28], процесс пластической деформации с упрочнением (рис.6.16), поскольку постулат Друкера обобщает выводы относительно монотонно упрочняющихся сред.
Пусть
элементарный объем деформируемого
тела, способного упрочняться, находится
в некотором исходном напряженном
состянии
.
Увеличим степень деформации этого
элементарного объема, что приведет к
возникновению добавочных напряжений,
а затем снимем их. Будем считать, что
процесс идет достаточно медленно для
того, чтобы он был изотермическим. При
выполнении этих условий Д.Друкер
постулировал, что при любом напряженном
состоянии:
1. В процессе нагружения добавочные напряжения производят положительную работу.
2. За весь цикл дополнительного нагружения и разгрузки добавочные напряжения выполняют положительную работу, если возникли плас-тические деформации; работа будет равна нулю только при упругих деформациях.
Из постулата Друкера следует ряд важных неравенств. Пусть F – текущее положение поверхности нагружения в 9ти-мерном пространстве напряжений (рис.6.18):
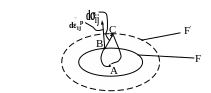
Рисунок 6.18 − К обоснованию постулата Друкера
Рассмотрим
некоторый путь нагружения от начальной
точки А с напряженным состоянием
в упругой зоне до точки В в пластической
зоне, лежащей на поверхности текучести.
Из состояния в точке В произведем
бесконечно малое догружение
,
вызывающее соответствующие упругую
и
пластическую
деформации.
Поскольку материал изотропно упрочняем,
то поверхность текучести равномерно
расширяется (эффектом Баушингера
пренебрегаем, следовательно, трансляционное
смещение будет отсутствовать) и новое
напряженное состояние будет изображаться
точкой С на поверхности F′(рис.6.18).
Затем осуществим разгрузку по какому
либо пути СА. В соответствии с постулатом
Друкера работа добавочных напряжений
за весь цикл положительна, т.е. интеграл:
Т.к. цикл АВСА замкнут, то работа добавочных напряжений на упругих деформациях равна нулю. Поэтому:
Поскольку пластические деформации происходят только на бесконечно малом участке ВС, то последнее неравенство можно представить в виде:
(6.23)
Это неравенство называется локальным принципом максимума.
Равенство нулю для упрочняющихся материалов возможно только при упругих деформациях.
Если цикл нагружения-разгрузки будет начинаться в точке В с исходным напряженным состоянием на поверхности F, то вследствие постулата Друкера:
1.
Для нагружения ВС -
2. Для нагружения и разгрузки ВСВ - .
Согласно
(6.23) скалярное произведение вектора
добавочных напряжений
(вектора АВ по рис.6.19а) и вектора
приращений пластических деформаций
положительно.
Следовательно, эти векторы всегда
должны образовывать между собой острый
угол. Отсюда вытекает необходимость
выпуклости поверхности нагружения (см.
п.6.3) и нормальность вектора
к
поверхности F.
Действительно, если поверхность нагружения F выпукла, то ус-
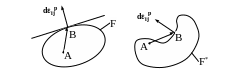
а) б)
Рисунок 6.19 − Обоснование выпуклости поверхности нагружения
ловие
(6.23) будет выполняться только в том
случае, когда вектор
нормален
к F.
В противном случае всегда можно найти
вектор
,
образующий с
тупой
угол. В крайнем случае, когда
совпадает с касательной к F,
работа (6.23) будет равна нулю (см. ниже).
Если поверхность нагружения F* не выпукла (рис.6.19б), то неза-
висимо от наклона к поверхности F*, всегда можно найти найти точку А такую, что вектор будет образовывать с тупой угол, что противоречит постулату Друкера. Отсюда вытекает необходимость ассоциированного закона течения.
Суть
его в следующем. Уравнения теории течения
можно представить через пластический
потенциал
в 9-мерном пространстве напряжений:
(6.24)
По
условию несжимаемости
,
поскольку пластическое изменение объема
пренебрежимо мало. Отсюда:
Пластический
потенциал – это некоторая скалярная
функция в пространстве напряжений,
частные производные от которой дают
величины, пропорциональные компонентам
приращений пластической деформации.
Иначе говоря, градиент от
по векторному аргументу
дает
вектор, пропорцииональный
(
имеется ввиду, что тензор напряжений в
9-мерном пространстве напряжений является
вектором с 9 компонентами). Уравнение
определяет
поверхности уровня пластического
потенциала. Т.к. градиент всегда нормален
к поверхности уровня, то (6.24) означает,
что вектор пластического течения
всегда
направлен по нормали к поверхности
пластического потенциала.
Далее
постулируется, что функция текучести
и пластический потенциал
совпадают:
Это простейший вариант теории; в нем легко доказываются теоремы существования и устанавливаются экстремальные принципы. Поэтому:
(6.25)
Отсюда следует, что пластическое течение развивается по нормали к поверхности течения (рис.6.21а).
Если принимается условие пластичности Губера-Мизеса:
то тогда:
,
и уравнения (6.25) принимают вид:
Это не что иное, как вторая предпосылка теории течения.
Зависимости (6.25) называются ассоциированным законом течения, поскольку в нем пластическое течение ассоциируется с условием текучести. Ассоциированный закон позволяет легко получать новые варианты теории течения посредством введения условий пластичности более сложного вида, чем условие Губера-Мизеса.
Следовательно, постулат Друкера требует выпуклости поверхности текучести и нормальности вектора пластического течения к поверхности F, т.е. ассоциированного закона течения.
В
случае идеальной пластичности (диаграмма
рис.6.9) поверх-ность нагружения фиксирована.
Поскольку в этом случае в пластической
области
,
то работа деформирования
Вектор
догружения
должен лежать в касательной плоскости
к поверхности текучести и должен вызывать
одни только упругие деформации. Это
следует из необходимости непрерывного
перехода пластических деформаций в
упругие при непрерывном изменении
направления вектора догружения и
называется условием непрерывности.
Поскольку работа деформирования равна
нулю, то требование положительности
работы добавочных напряжений заменяется
требованием ее неотрицательности. В
таком виде постулат Друкера справедлив
и для идеально-пластических сред.
Неравенство (6.23) приобретает вид:
Что касается случая деформации с разупрочнением, то постулат
Друкера, в существующем виде, к нему не применим. Если же разупрочнение анизотропно, то сомнительна применимость и всей теории течения.