
- •8 Приложения. Элементы векторной и тензорной алгебры
- •1.1 Задачи курса «Механика сплошных сред»
- •1.2 Предмет механики сплошной среды
- •1.3 Методы механики сплошной среды
- •1.4 Основные принципы механики сплошной среды
- •1.5 Элементарный объем
- •1.6 Переменные Лагранжа и Эйлера
- •1.7 Движение и равновесие сплошной среды
- •2 Статика сплошной среды
- •2.1 Напряжение в точке
- •2.2 Напряженное состояние в точке
- •2.3 Соотношения Коши и компоненты напряженного
- •2.4 Тензор напряжений
- •2.5 Доказательство тензорности напряженного состояния*
- •2.6 Условия симметричности тензора напряжений
- •2.7 Доказательство равенства парных касательных
- •2.8 Общий случай напряженного состояния*
- •2.9 Главные напряжения
- •2.10 Нормальные и касательные напряжения
- •2.11 Максимальные касательные напряжения
- •2.12 Шаровой тензор и девиатор напряжений
- •2.13 Изображение напряженного состояния в точке
- •2.14 Октаэдрические напряжения и интенсивности
- •2.15 Уравнения равновесия
- •2.16 Уравнения равновесия в недекартовых системах
- •2.17 Уравнения равновесия в общем случае *
- •2.18 Краевая задача статики сплошной среды
- •3 Кинематика сплошной среды
- •3.2 Абсолютная и относительная деформация
- •3.3 Поле относительных смещений
- •3.4 Составляющие движения сплошной среды
- •3.5 Тензор малых деформаций
- •3.6 Геометрический смысл компонент тензора малых
- •3.7 Тензоры конечных деформаций
- •3.8 Общий случай малых деформаций *
- •3.9 Анализ деформированного состояния в точке
- •3.10 Инварианты тензора малых деформаций
- •3.11 Главные деформации
- •3.12 Максимальные угловые деформации
- •3.13 Октаэдрические деформации и интенсивности
- •3.14 Условия совместности деформаций
- •3.15 Определение перемещений по деформациям*
- •3.16 Поле скоростей
- •3.17 Первая теорема Гельмгольца
- •3.18 Тензор скоростей деформаций
- •3.19 Свойства тензора скоростей деформаций
- •3.20 Вторая теорема Гельмгольца*
- •4 Элементы термодинамики сплошных сред
- •4.1 Термодинамические системы и параметры состояния
- •4.2 Законы сохранения
- •4.3 Теоремы э. Нётер и свойства симметрии
- •4.4 Закон сохранения массы и уравнение неразрывности
- •4.5 Вывод уравнения неразрывности*
- •4.6 Теорема «живых сил»
- •4.7 Первое начало термодинамики
- •4.8 Уравнение теплопроводности
- •5 Основы теории упругости
- •5.1 Предмет теории упругости
- •5.2 Обобщенный закон Гука
- •5.3 Упругое изменение объема и формы
- •5.4 Потенциальная энергия упругого деформирования
- •5.5 Постановка задач в теории упругости
- •5.6 Решение задач теории упругости в перемещениях
- •5.7 Решения задач теории упругости в напряжениях
- •5.8 Плоское напряженное состояние*
- •5.9 Плоское деформированное состояние*
- •5.10 Плоская задача в моментной теории упругости *
- •5.11 Функция напряжений*
- •5.12 Способы решения задач теории упругости*
- •6 Основы теории пластичности
- •6.1 Предмет теории пластичности
- •6.2 Переход в пластическое состояние при растяжении
- •6.3 Условия пластичности
- •6.6 Экспериментальная проверка условий
- •6.7 Теории пластичности
- •6.8 Теория пластического течения
- •6.10 Постулат Друкера и ассоциированный закон
- •6.11 Области применимости различных теорий пластичности
- •6.12 Экстремальные принципы пластического
- •7 Применение теории пластичности в омд
- •7.1 Постановка задач при расчетах процессов омд
- •7.2 Математический аппарат и краевые условия при омд
- •7.3 Способы решения задач теории пластичности
- •1.Численные методы;
- •2.Прямые методы получения решений на основе экстремальных принципов мсс;
- •3.Уменьшения числа независимых переменных и искомых функций.
- •7.4 Частные виды напряженно-деформированных
- •1. Толщина пластины значительно меньше остальных размеров;
- •2. Деформирующие усилия приложены в срединной плоскости пластины.
- •7.5 Особенности плоского деформированного состояния
- •7.6 Осесимметричное деформированное состояние
- •7.7 Метод линий скольжения
- •7.8. Свойства линий скольжения
- •7.9 Простые сетки линий скольжения
- •7.10 Статические граничные условия в млс
- •7.11 Задача о внедрении штампа в полупространство
- •7.12 Основные краевые задачи в млс*
- •7.13 Определение поля скоростей в млс*
- •7.14 Полные решения задач плоской деформации
- •Пластичности в омд”
- •8. Приложения. Элементы векторной и тензорной алгебры и анализа
- •8.1 Скаляры и векторы
- •8.2 Векторный базис
- •8.3 Сложение и умножение векторов
- •8.4 Тензоры 2-го ранга
- •8.5 Преобразование компонент тензора
- •8.6 Сложение и умножение тензоров
- •8.7 Симметрирование и альтернирование тензоров
- •8.8 Умножение тензора на вектор
- •8.9 Главные оси тензора
- •8.10 Определение величины и направления главных компонент тензора
- •8.12 Поверхности уровня и градиент скалярного поля
- •8.13 Векторное поле и векторные линии
- •8.14 Поток и дивергенция векторного поля
- •Теорема Остроградского–Гаусса:
- •8.15 Циркуляция и ротор векторного поля
- •8.16 Оператор («набла»)
- •8.17 Дифференциальные операции 2-го порядка
- •8.18 Потенциальные векторные поля
- •8.20 Гармонические векторные поля
- •8.21 Основная теорема векторного анализа
- •8.22 Производная и градиент векторного поля
- •8.23 Поток тензорного поля
- •8.24 Дивергенция тензорного поля
- •8.25 Производная тензорного поля по направлению
- •Предметный указатель
- •Перечень ссылок
4.4 Закон сохранения массы и уравнение неразрывности
Закон сохранения массы является одним из фундаментальных законов классической физики. Установлен он опытным путем и в макромире выполняется с очень высокой степенью точности.
Масса любой изолированной физической системы не измняется со временем.
Формально он может быть записан в виде:
![]() ,
,
где m – масса физической системы.
Однако в МСС, где приходится иметь дело с телами, непрерывно заполняющими некоторые части пространства, вместо массы исполь-зуется понятие плотности сплошной среды.
Предел отношения массы m некоторого объема W сплошной
среды к этому объему при его стремлении к нулю называется плотностью среды в точке, к которой стягивается данный объем:
![]()
Используя понятие плотности, закон сохранения массы можно выразить следующим образом:
![]() (4.1)
(4.1)
При решении задач МСС закон сохранения массы обычно используется в виде дифференциального уравнения, именуемого уравнением неразрывности в переменных Эйлера:
![]() (4.2)
(4.2)
Оно выражает закон сохранения массы в дифференциальной форме. Если среда однородна и ее плотность не изменяется со временем (что с достаточной для практики точностью имеет место у металлов в пластическом состоянии), то уравнение неразрывности превращается в уравнение несжимаемости:
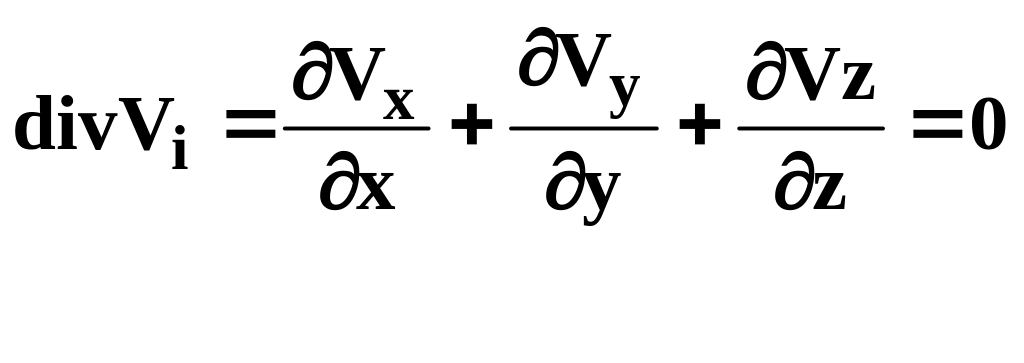 (4.3)
(4.3)
4.5 Вывод уравнения неразрывности*
Чтобы получить уравнение неразрывности, рассмотрим изменение плотности частиц сплошной среды со временем.
Распределение
плотности в сплошной среде можно задать
как с точки зрения Лагранжа, так и с
точки зрения Эйлера. В первом случае
![]() и изменение плотности будет частной
производной по времени
и изменение плотности будет частной
производной по времени
![]() ,
т.к. плотность у частицы, а не у точки
пространства. Координаты частицы
(переменные Лагранжа) при этом постоянны.
,
т.к. плотность у частицы, а не у точки
пространства. Координаты частицы
(переменные Лагранжа) при этом постоянны.
В переменных Эйлера плотность будет функцией координат точек пространства и времени ρ = ρ (х,у,z,τ) и для вычисления той же величины сначала нужно перейти к переменным Лагранжа:
ρ (х,у,z,τ) = ρ [ x (х,у,z,τ); y (х,у,z,τ); z (х,у,z,τ); τ ]
Затем уже можно найти изменение плотности индивидуальной частицы с точки зрения Эйлера, используя правило дифференцирования сложной функции и учитывая, что в данном случае аргументы х, у, z являются функциями только одной переменной τ (т.к. xi = соnst).
Из математики известно, что если функция нескольких переменных F=F(u,v,w,τ) в качестве своих агументов имеет функции u = u (х,у,z,τ); v = v (х,у,z,τ); w = w (х,у,z,τ), и если аргументы u, v, w в частном случае зависят только от одной переменной, например τ, то тогда функция F (u, v, w, τ) является функцией фактически только одной переменной τ. В этом случае ее обыкновенная производная называется полной и она имеет вид:
![]()
Поэтому в нашем случае:
![]() (4.4)
(4.4)
В
(4.4) производные
![]() являются компонентами вектора скорости
являются компонентами вектора скорости
Vi , т.к. берутся при постоянных Xi. Отсюда:
![]() (4.5)
(4.5)
Производная
![]() характеризует
изменение во времени плотности частицы
сплошной среды и называется субстанциональной
или индивидуальной производной.
Производная
характеризует
изменение во времени плотности частицы
сплошной среды и называется субстанциональной
или индивидуальной производной.
Производная
![]() характеризует изменение плотности в
данной точке пространства и называется
локальной или местной производной.
Выражению
характеризует изменение плотности в
данной точке пространства и называется
локальной или местной производной.
Выражению
![]() можно придать вид: Vi
grad
ρ.
Оно называется конвективной производной
по времени и характеризует изменение
плотности за счет перемещения частиц
сплошной среды разной плотности из
одной точки пространства в другую.
можно придать вид: Vi
grad
ρ.
Оно называется конвективной производной
по времени и характеризует изменение
плотности за счет перемещения частиц
сплошной среды разной плотности из
одной точки пространства в другую.
Произведя перегруппировку членов в (4.5), получим искомое выражение для изменения плотности во времени с точки зрения Эйлера:
![]() =
– Vi
grad
ρ
+
=
– Vi
grad
ρ
+
![]()
Из него видно, что изменение плотности в некоторой точке пространства хi обусловлено, во-первых, переносом (приходом в нее новых частиц с иной плотностью), а во-вторых – изменением плотности самих частиц с течением времени.
Перенос описывается конвективной производной. Она может быть равна нулю, когда нет движения сплошной среды (Vi = 0), или когда поле плотности (или любой другой скалярной функции, например, температуры), однородно (grad ρ = 0). Если поле стационарно, то равна нулю субстанциональная производная и изменение плотности в
точке пространства полностью обусловлено переносом.
Теперь рассмотрим изменение во времени интеграла:
![]() (4.6)
(4.6)
Оно
происходит как от изменения плотности
ρ,
так и объема W,
поскольку интеграл берется по объему
части среды, а не пространства (по т.н.
«подвижному объему»). Если бы объем W
был постоянен, то за время dτ
функция
ρ получила
бы приращение![]() ,а
интеграл - приращение:
,а
интеграл - приращение:
![]()
Если функция ρ остается неизменной, а изменяется объем W ,то это происходит потому, что некоторые частицы сплошной среды входят или выходят через поверхность F в объем W (рис.4.2).
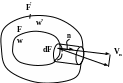
Рисунок 4.2 − Изменение плотности за счет переноса
Через элемент dF этой поверхности за время dτ может выйти
объем
![]() .
За счет этого интеграл (4.6) получит
приращение:
.
За счет этого интеграл (4.6) получит
приращение:
![]() .
.
Следовательно, полное приращение интеграла будет равно:
![]()
Его производная по времени:
![]() (4.7)
(4.7)
Используя теорему Остроградского–Гаусса, преобразуем 2-й интеграл в объемный:
![]()
После подстановки в (4.7) и учета (4.5) имеем:
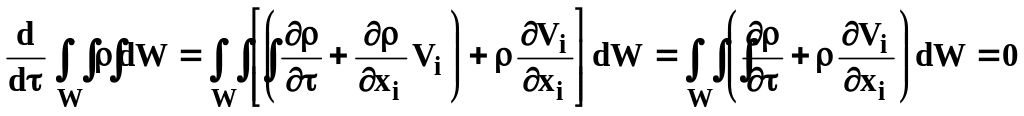
Поскольку объем W был взят произвольным, то:
![]()
Учитывая,
что
![]() ,
окончательно получим:
,
окончательно получим:
![]() ,
,
что и требовалось.
