
- •8 Приложения. Элементы векторной и тензорной алгебры
- •1.1 Задачи курса «Механика сплошных сред»
- •1.2 Предмет механики сплошной среды
- •1.3 Методы механики сплошной среды
- •1.4 Основные принципы механики сплошной среды
- •1.5 Элементарный объем
- •1.6 Переменные Лагранжа и Эйлера
- •1.7 Движение и равновесие сплошной среды
- •2 Статика сплошной среды
- •2.1 Напряжение в точке
- •2.2 Напряженное состояние в точке
- •2.3 Соотношения Коши и компоненты напряженного
- •2.4 Тензор напряжений
- •2.5 Доказательство тензорности напряженного состояния*
- •2.6 Условия симметричности тензора напряжений
- •2.7 Доказательство равенства парных касательных
- •2.8 Общий случай напряженного состояния*
- •2.9 Главные напряжения
- •2.10 Нормальные и касательные напряжения
- •2.11 Максимальные касательные напряжения
- •2.12 Шаровой тензор и девиатор напряжений
- •2.13 Изображение напряженного состояния в точке
- •2.14 Октаэдрические напряжения и интенсивности
- •2.15 Уравнения равновесия
- •2.16 Уравнения равновесия в недекартовых системах
- •2.17 Уравнения равновесия в общем случае *
- •2.18 Краевая задача статики сплошной среды
- •3 Кинематика сплошной среды
- •3.2 Абсолютная и относительная деформация
- •3.3 Поле относительных смещений
- •3.4 Составляющие движения сплошной среды
- •3.5 Тензор малых деформаций
- •3.6 Геометрический смысл компонент тензора малых
- •3.7 Тензоры конечных деформаций
- •3.8 Общий случай малых деформаций *
- •3.9 Анализ деформированного состояния в точке
- •3.10 Инварианты тензора малых деформаций
- •3.11 Главные деформации
- •3.12 Максимальные угловые деформации
- •3.13 Октаэдрические деформации и интенсивности
- •3.14 Условия совместности деформаций
- •3.15 Определение перемещений по деформациям*
- •3.16 Поле скоростей
- •3.17 Первая теорема Гельмгольца
- •3.18 Тензор скоростей деформаций
- •3.19 Свойства тензора скоростей деформаций
- •3.20 Вторая теорема Гельмгольца*
- •4 Элементы термодинамики сплошных сред
- •4.1 Термодинамические системы и параметры состояния
- •4.2 Законы сохранения
- •4.3 Теоремы э. Нётер и свойства симметрии
- •4.4 Закон сохранения массы и уравнение неразрывности
- •4.5 Вывод уравнения неразрывности*
- •4.6 Теорема «живых сил»
- •4.7 Первое начало термодинамики
- •4.8 Уравнение теплопроводности
- •5 Основы теории упругости
- •5.1 Предмет теории упругости
- •5.2 Обобщенный закон Гука
- •5.3 Упругое изменение объема и формы
- •5.4 Потенциальная энергия упругого деформирования
- •5.5 Постановка задач в теории упругости
- •5.6 Решение задач теории упругости в перемещениях
- •5.7 Решения задач теории упругости в напряжениях
- •5.8 Плоское напряженное состояние*
- •5.9 Плоское деформированное состояние*
- •5.10 Плоская задача в моментной теории упругости *
- •5.11 Функция напряжений*
- •5.12 Способы решения задач теории упругости*
- •6 Основы теории пластичности
- •6.1 Предмет теории пластичности
- •6.2 Переход в пластическое состояние при растяжении
- •6.3 Условия пластичности
- •6.6 Экспериментальная проверка условий
- •6.7 Теории пластичности
- •6.8 Теория пластического течения
- •6.10 Постулат Друкера и ассоциированный закон
- •6.11 Области применимости различных теорий пластичности
- •6.12 Экстремальные принципы пластического
- •7 Применение теории пластичности в омд
- •7.1 Постановка задач при расчетах процессов омд
- •7.2 Математический аппарат и краевые условия при омд
- •7.3 Способы решения задач теории пластичности
- •1.Численные методы;
- •2.Прямые методы получения решений на основе экстремальных принципов мсс;
- •3.Уменьшения числа независимых переменных и искомых функций.
- •7.4 Частные виды напряженно-деформированных
- •1. Толщина пластины значительно меньше остальных размеров;
- •2. Деформирующие усилия приложены в срединной плоскости пластины.
- •7.5 Особенности плоского деформированного состояния
- •7.6 Осесимметричное деформированное состояние
- •7.7 Метод линий скольжения
- •7.8. Свойства линий скольжения
- •7.9 Простые сетки линий скольжения
- •7.10 Статические граничные условия в млс
- •7.11 Задача о внедрении штампа в полупространство
- •7.12 Основные краевые задачи в млс*
- •7.13 Определение поля скоростей в млс*
- •7.14 Полные решения задач плоской деформации
- •Пластичности в омд”
- •8. Приложения. Элементы векторной и тензорной алгебры и анализа
- •8.1 Скаляры и векторы
- •8.2 Векторный базис
- •8.3 Сложение и умножение векторов
- •8.4 Тензоры 2-го ранга
- •8.5 Преобразование компонент тензора
- •8.6 Сложение и умножение тензоров
- •8.7 Симметрирование и альтернирование тензоров
- •8.8 Умножение тензора на вектор
- •8.9 Главные оси тензора
- •8.10 Определение величины и направления главных компонент тензора
- •8.12 Поверхности уровня и градиент скалярного поля
- •8.13 Векторное поле и векторные линии
- •8.14 Поток и дивергенция векторного поля
- •Теорема Остроградского–Гаусса:
- •8.15 Циркуляция и ротор векторного поля
- •8.16 Оператор («набла»)
- •8.17 Дифференциальные операции 2-го порядка
- •8.18 Потенциальные векторные поля
- •8.20 Гармонические векторные поля
- •8.21 Основная теорема векторного анализа
- •8.22 Производная и градиент векторного поля
- •8.23 Поток тензорного поля
- •8.24 Дивергенция тензорного поля
- •8.25 Производная тензорного поля по направлению
- •Предметный указатель
- •Перечень ссылок
3.14 Условия совместности деформаций
Компоненты тензора малых деформаций, выраженные через компоненты тензора относительных смещений, называются дифференциальными зависимостями Коши (не путать с соотношениями Коши):
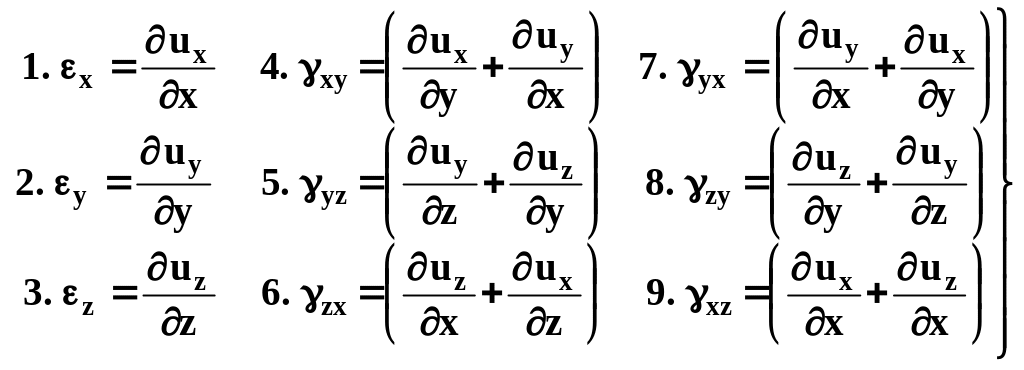 (3.35)
(3.35)
Они позволяют по известным компонентам дифференцированием находить компоненты малой деформации. Чаще, однако, возникает обратная задача: по компонентам εij найти компоненты ui . Решить ее, используя только (3.35) невозможно, т.к. система уравнений переопределена: для 3-х компонент ui имеется девять формул. Чтобы решение стало возможным, нужно устранить переопределенность системы (3.35), наложив на компоненты εij шесть ограничивающих условий таких, чтобы результаты интегрирования соотношений Коши не зависели от пути интегрирования. Геометрически это означает, что компоненты деформируемого тела должны быть связаны между собой таким образом, чтобы после деформации из этих элементарных объемов мож-но было сложить сдеформированное тело без разрывов и наложений частиц друг на друга (рис.3.15).


→ ↓

←
Рисунок 3.15 − К условию неразрывности
Чтобы получить указанные соотношения, продифференцируем
первые два уравнения системы (3.35) дважды по противоположным
индексам:
![]()
![]()
Складывая их почленно, получим:
![]() +
+
![]() .
.
Это – уравнение совместности деформаций в плоскости ХОУ. Аналогично получаются уравнения совместности в плоскостях УОZ и ZОХ.
Чтобы получить уравнения совместности в разных плоскостях, продифференцируем 4, 5 и 6-е уравнения (3.35):
![]()
![]()
![]()
Сложив
два последних соотношения и вычтя
первое, продифферен-ировав полученное
по
![]() и
учтя, что:
и
учтя, что:
![]() ,
,
получим:
![]()
Аналогично находятся еще два уравнения. В итоге имеем систему 6 уравнений, называемую условиями совместности деформаций или уравнениями Сен-Венана, гарантирующими получение непрерывного тела после деформации в соответствии с принципом сплошности. Из них следует, что каждые две линейные деформации определяют соот-
ветствующую угловую, а каждые три угловые – одну линейную:
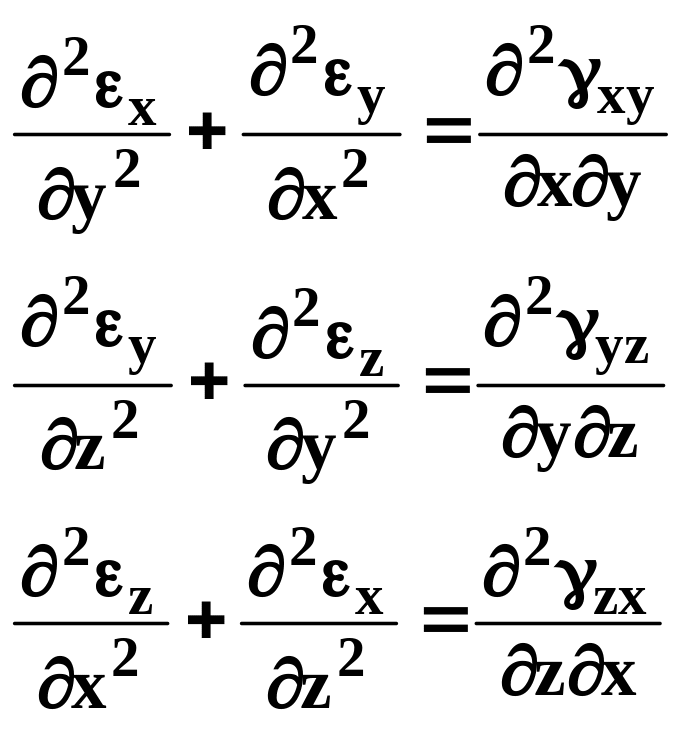 (3.36)
(3.36)
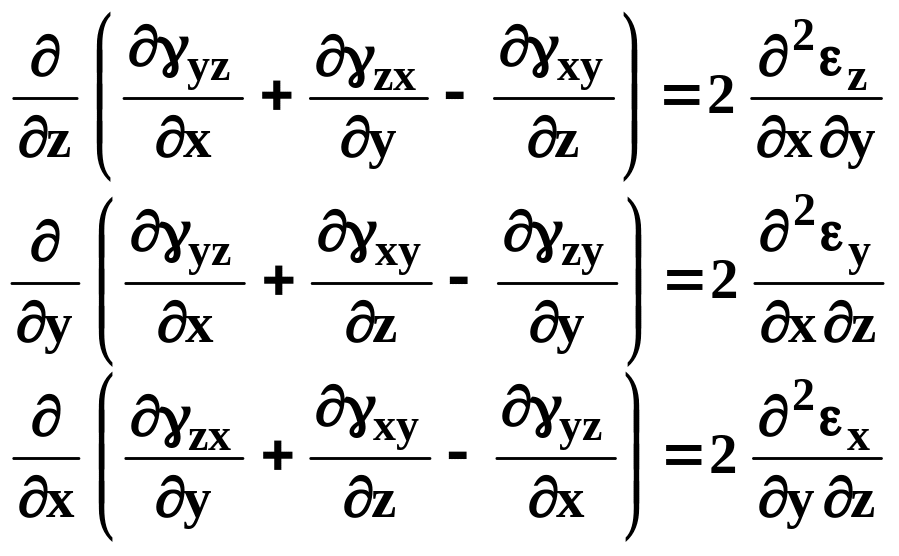 .
.
Уравнения Сен-Венана являются необходимыми и достаточными условиями интегрируемости соотношений (3.35) только в случае односвязной области. Если область многосвязна, например двухсвязна (рис. 3.16), то (3.36) являются только необходимыми условиями.
Рисунок 3.16 − Превращение двухсвязной области в односвязную
Для достаточности их нужно дополнить условием равенства сме-
щений
по обе стороны разреза АВ,
превращающего данную двухсвязную
область в две одно связные:
![]() .
.
В общем случае, когда кроме удлинений и сдвигов имеются также искривления граней, последние должны учитываться в условиях совместности деформаций.
