1.4.8. Бета-розподіл
Випадкова
величина X
має бета-розподіл з параметрами α і β
якщо її щільність імовірності обчислюється
за формулою
(1.52)
Тут
і далі
– гамма-функція Ейлера.
Для
цієї випадкової величини
Якщо
то бета-розподіл одномодальний з модою
у точці
При
бета-розподіл є рівномірним розподілом
на інтервалі
Унаслідок того, що бета-розподіл приймає різні форми, він використовується для опису великої кількості реальних випадкових величин при контролі якості продукції, у теорії надійності, для оцінки тривалості певного етапу роботи при календарному плануванні.
Криві
бета-розподілу для різних значень
параметрів
і
наведені на
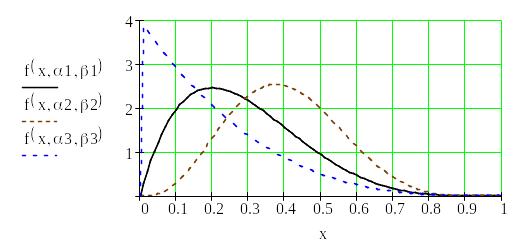
Рис. 1.8. Щільність бета-розподілу
У математичній статистиці бета-розподіл найбільш часто зустрічається у якості розподілу порядкових статистик.
Функції Mathcad для роботи з бета–розподілом: dbeta(), pbeta(), qbeta(), rbeta().
1.4.9. Гамма-розподіл
Випадкова
величина
має гамма-розподіл з параметрами
якщо її щільність імовірності обчислюється
за формулою:
(1.53)
Математичне сподівання і дисперсія цієї величини дорівнюють:
При
мода розподілу знаходиться у нулі, а
при
у
точці
Якщо
то гамма-розподіл співпадає з
експоненціальним розподілом, а при
з розподілом
з
ступенями свободи. У випадку
і
(
натуральне число) цей розподіл називають
розподілом
Ерланга
з параметрами
і
Гамма-розподіл і його частинні випадки широко використовуються у теорії ймовірностей і математичній статистиці.
Графіки
розподілу для
різних значень параметрів
наведені на рис. 1.9.
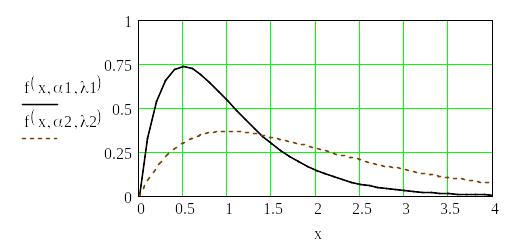
Рис. 1.9. Щільність гамма-розподілу
Функції Mathcad для роботи з гамма–розподілом: dgamma(), pgamma(), qgamma(), rgamma().
1.4.10. Розподіл
Розподілом з ступенями свободи називається розподіл суми квадратів незалежних випадкових величин, розподілених за стандартним нормальним законом, тобто
де
мають нормальний розподіл
Щільність імовірності - розподілу обчислюється за формулою
(1.54)
Для даного розподілу математичне сподівання, дисперсія, коефіцієнт асиметрії і ексцес дорівнюють
При
мода знаходиться у точці
Криві – розподілу, побудовані у Mathcad, для різних значень кількості ступенів свободи наведені на рис. 1.10.
У математичній статистиці розподіл застосовується при побудові цілої низки різноманітних критеріїв, у тому числі при перевірці гіпотез узгодженості вибіркових даних з вибраним законом розподілу та в методі найменших квадратів.
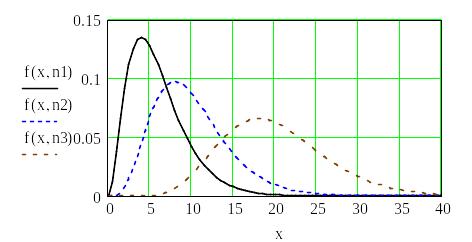
Рис. 1.10. Щільність розподілу
Функції Mathcad
для роботи з розподілом
:
dchisq(), pchisq(),
qchisq(),
1.4.11. Розподіл Стьюдента
Розподілом Стьюдента
(або
розподілом)
називається розподіл випадкової величини
,
де
випадкова
величина, розподілена за стандартним
нормальним законом, тобто
– незалежна від
випадкова величина, яка має
-
розподіл з
ступенями свободи.
Щільність імовірності розподілу Стьюдента має вигляд:
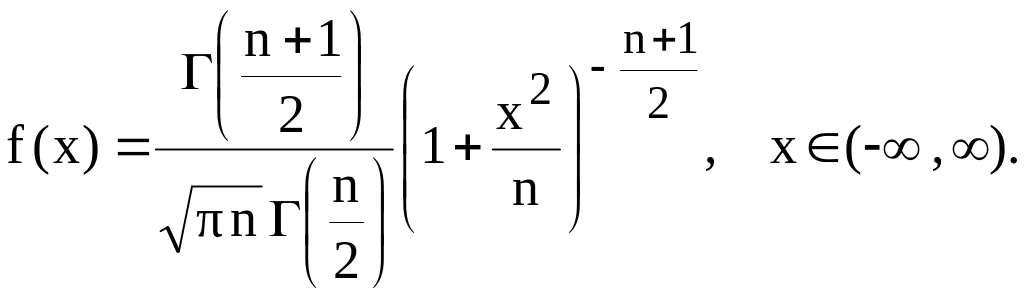(1.55)
Математичне сподівання, дисперсія, коефіцієнт асиметрії і ексцес дорівнюють
При великих значеннях розподіл Стьюдента асимптотично наближається до нормального розподілу.
Розподіл Стьюдента має багаточисельні застосування у математичній статистиці при побудові інтервальних оцінок параметрів розподілів, при побудові критеріїв перевірки статистичних гіпотез.
Функції Mathcad для роботи з розподілом Стьюдента: dt(), pt(), qt(), r().
Криві
розподілу
для різних значень кількості ступенів
свободи
наведені на рис. 1.11.
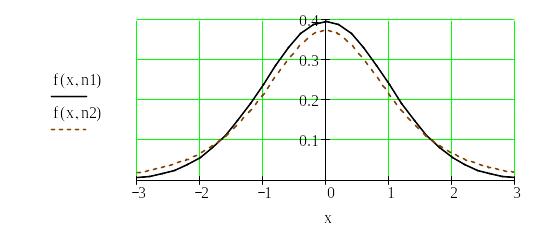
Рис. 1.11. Щільність розподілу Стьюдента
1.4.12. F – розподіл Фішера-Снедекора
Розподілом
Фішера-Снедекора (або
розподілом)
з
ступенями свободи
називається розподіл випадкової величини
де
і
випадкові величини, які мають
розподіл
відповідно з
і
ступенями свободи.
Щільність імовірності розподілу має вигляд:
(1.56)
Математичне сподівання і дисперсія дорівнюють
При
мода знаходиться у точці
розподіл відіграє основну роль при порівнянні вибіркових дисперсій із нормально розподілених сукупностей. Він також широко використовується у регресійному та дисперсійному аналізі.
Графіки
–
розподілу для різних значень кількості
ступенів свободи
і
наведені на рис. 1.12.
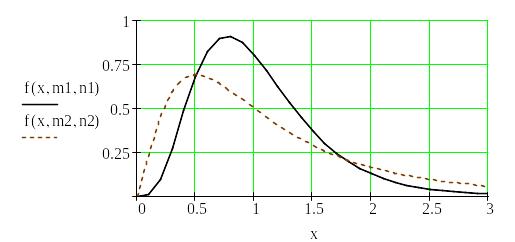
Рис. 1.12. Щільність розподілу
Функції Mathcad для роботи з F – розподілом: df(), pf(), qf(), rf().