1.4. Основні закони розподілу

Наведемо основні закони розподілів дискретних і неперервних випадкових величин, які використовуються для побудови ймовірнісно-статистичних моделей різних явищ і процесів.

1.4.1. Біноміальний розподіл

Випадкова величина X має біноміальний розподіл з параметрами n і p якщо вона приймає значення з імовірностями, які визначаються за формулою Бернуллі

(1.40)

– біноміальні коефіцієнти.

Математичне сподівання і дисперсія біноміально розподіленої величини дорівнюють:

Графіки розподілу для різних значень параметрів і наведені на

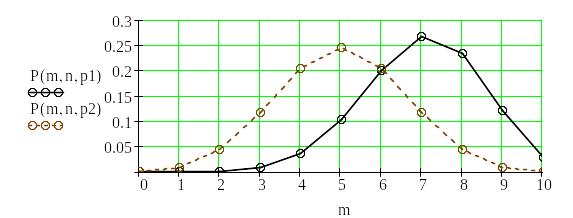
Рис. 1.1. Біноміальний розподіл

Біноміальний розподіл є моделлю випадкових експериментів, які складаються із n незалежних однакових випробувань. У результаті кожного з них з імовірністю p може здійснитись подія А і з імовірністю – протилежна подія. Прийнятою назвою для такої моделі випадкових експериментів є схема Бернуллі. Біноміальний розподіл широко використовується у теорії і практиці статистичного контролю якості продукції, у теорії масового обслуговування й інших прикладних областях математичної статистики.

Функції Mathcad для роботи з біноміальним розподілом: dbinom(), qbinom(), rbinom().

1.4.2. Гіпергеометричний розподіл

Випадкова величина Х має гіпергеометричний розподіл з параметрами , якщо

(1.41)

де біноміальні коефіцієнти,

Для будь-яких значень параметрів, які входять у розподіл

Для цього розподілу математичне сподівання і дисперсія дорівнюють

Існує і інша форма цього розподілу. Нехай де

, тоді

,

У цьому випадку

Типова ситуація, де з’являється гіпергеометричний розподіл, така: перевіряється партія готової продукції об’ємом у якій виробів стандартні і нестандартні. Якщо випадковим чином із усієї партії вибрати контрольну партію із виробів, то кількість стандартних виробів у цій партії буде випадковою величиною можливі значення якої мають гіпергеометричний розподіл.

Графік розподілу для значень параметрів наведений на рис. 1.2.

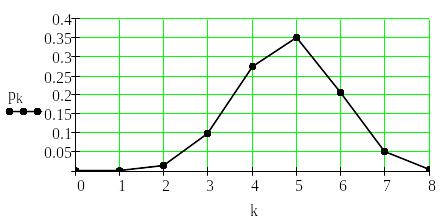
_{Рис. 1.2. Гіпергеометричний розподіл}

Гіпергеометричний розподіл широко використовується у практиці статистичного приймального контролю якості продукції, у задачах, пов’язаних із організацією вибіркових досліджень, і інших областях.

Функції Mathcad для роботи з гіпергеометричним розподілом:

1.4.3. Розподіл Пуассона

Дискретна випадкова величина X має розподіл Пуасcона з параметром якщо вона приймає значення з імовірностями

(1.42)

Для цього розподілу математичне сподівання і дисперсія співпадають, тобто

Графік розподілу для різних значень параметра наведений на рис. 1.3.

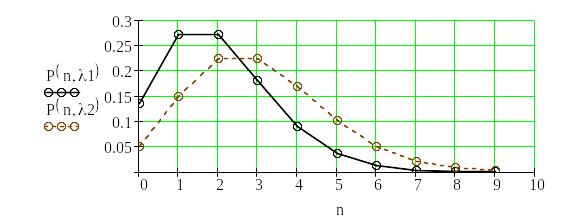
Рис. 1.3. Розподіл Пуассона

Розподіл Пуассона виникає при наступних обставинах. Нехай здійснюється незалежних випробувань, у кожному з яких імовірність появи події дорівнює Для визначення імовірності появ події у цих випробуваннях використовують формулу Бернуллі. Якщо ж велике і ймовірність події мала то прибігають до асимптотичної формули Пуассона.

Розподіл Пуаcсона відіграє важливу роль при моделюванні випадкових потоків подій. Він є моделлю для опису випадкової кількості появ певних подій у фіксований проміжок часу або у фіксованій області простору. Він широко застосовується у теорії масового обслуговування для опису вхідних і вихідних потоків, теорії надійності для характеристики кількості відмов елементів складних систем тощо.

Функції Mathcad для роботи з розподілом Пуассона: dpois (), ppois(), qpois(), rpois().