Рассмотрим вопрос об определении статистических численных характеристик случайных величин в энергетике.

Пусть имеется

статистический ряд наблюдений случайной величины, например, максимальной суточной нагрузки энергосистемы. Отдельные наблю­дения дают значения: х₁, х₂ , ...,x_n . Математическое ожидание и дисперсию определим по следующим формулам;

М*(х}= ∑х_i/n;

D*(x) = ∑{ x_i - ∑ x_i / n}² / (n-1).

Пример 3-15. Пусть, например, наблюдения максимальных нагрузок за 10 рабочих дней дают следующий ряд: 910, 921, 905, 917, 930, 911, 925, 914, 916, 921. Тогда

Μ*(x) = 917; D*(x) = 56 и δ*(х) = 7,5.

Довольно часто случайные величины являются зависимыми, при­чем определение одной величины более доступно, чем другой, от нее зависящей. Зависимость двух случайных величин отличается от обычного понимания функциональной зависимости двух неслучайных величин. Если одна из случайных величин принимает конкретное значение, то это не означает, что и другая принимает конкретное значение. Вторая величина является также случайной величиной, но ее вероятностные характеристики принимают те или иные зна­чения в зависимости от конкретного значения первой случайной величины. Такими случайными величинами в энергетике являются, например, суточная выработка энергии и суточный максимум на­грузки энергосистемы, суммарная нагрузка и температура наруж­ного воздуха, запас снега и паводковый сток реки и т. п.

Таким образом, если две случайные величины ε и η, принимаю­щие различные значения x и у, независимы, то закон распределения вероятностей одной из них не зависит от случайного значения дру­гой. Если же эти величины зависимы, то любому значению одной из них соответствует тот или иной закон распределения вероятно­стей другой величины. Зависимость закона распределения вероят­ностей одной величины от значения другой называется корреля­ционной зависимостью. Простейшим видом корреляционной зависи­мости является, например, известная зависимость м.о. веса взрослого человека от его роста, которая была ранее довольно популярна .в быту: М(y) = x – 100, где у—вес, кгс; x—рост, см.

Математическое ожидание случайной величины η при значении другой случайной взаимозависимой величины ε = x называется условным м.о.:

для дискретных величин

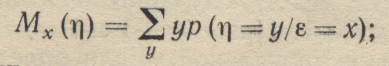(1-38)

Для непрерывных

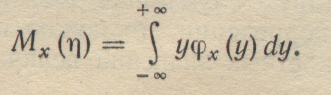(1-39)

В В (1-38) член p (η = у/ε= x) — это условная вероятность того, что когда случайная

величина ε принимает значение х, то случайная величина η получает значение у, где у охщхватывает все возможные значения η.

В (1-39) член φ_x(y)—это условная плотность вероятности, т.е. плотность вероятности η, если ε = x. Очевидно, что M_x(η) зависит от х, т. е. является функцией х:

Μ_x(η) = f (x) (1-40)

и называется функцией регрессии случайной величины η на случайную величину ε; уравнение |

y = f(x) (1-41)

называется уравнением регрессии.

Рассмотрим простейший случай линейной корреляции между двумя зависимыми случайными величинами [Л.2] . При этом уравнение регрессии случайной величины η на случайную ве­личину е имеет вид

М_x ( η) = ρ(η/ε)(x--α) +b, (1-42)

где x—значение случайной величины ε; α—м.о. случайной вели­чины ε; b—м.о. случайной величины η; ρ(η/ε)—коэффициент ре­грессии случайной величины η на ε;

ρ (η/ε) - [Μ (εη) - αb] / δ²_ε , (1-43)

Здесь δ_ε—стандартное отклонение ε.

Аналогично, ρ (ε/η) и δ_η. Введя в рассмотрение коэффициент корреляции

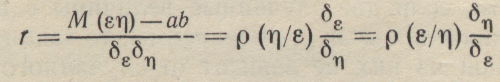(1-44)

получим выражения для м.о. случайной величины η, зависящей от величины ε;

М_x (η) = г (δ_η/δ_ε) (х - а) + Ь, (1-45)

где а и δ_ε—м.о. и стандартное отклонение величины ε ; b и δ_η—м.о. и стандартное отклонение величины η. Аналогично

M_y (ε) = r(δ_ε/δ_η) (y – b) + a.

При r·=0 исчезнет различие между M_x(η) и M(η), а также между Μ_y(ε) и Μ (ε).

Следовательно, коэффициент корреляции характеризует корреля­ционную зависимость между случайными величинами. Величина r изменяется от —1 до +1· При r=—1 или r = +1 корреляционная связь заменяется функциональной. Если определены м. о. и стан­дартное отклонение двух случайных зависимых величин η и ε, а также коэффициент корреляции, то можно найти зависимость м.о. величин η, ε от конкретных значений величин ε, η.

Для статистического определения коэффициента корреляции между двумя случайными величинами η и ε необходимо иметь ряд наблюдении этих величин. Пусть наблюдались следующие пары одновременных значений η и ε; y₁, x_1; у₂, х₂ ...; у_n х_n. Тогда для получения зависимости M_x(η) от x нужно найти а, b, δ_ε, δ_η и r по следующим формулам:

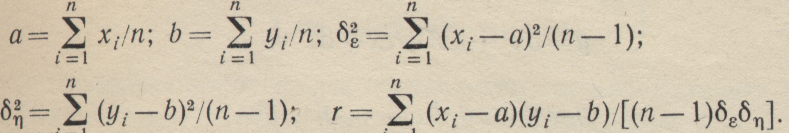(1-46)

Пример 3-16. В течение ряда лет максимум нагрузки энергосистемы Ρ(МВт) и годовая выработка электроэнергии W (млрд. кВт·ч) имели следующие значения:

ε Ρ 1000 1100 1220 1350 η W 5,6 6,6 7,0 7,8

Определим коэффициент корреляции двух случайных величин ε и η (Ρ и W), для чего по формуле (1-36) найдем статистическое м.о. ε и η:

а = М*(ε)=(1000+1100+1220+1350)/4=1167,5, b=M*(η)==(5,6+6,6+7,0+7,8)/4 = 6,75.

Далее по формуле (1-37) найдем статистические дисперсии:

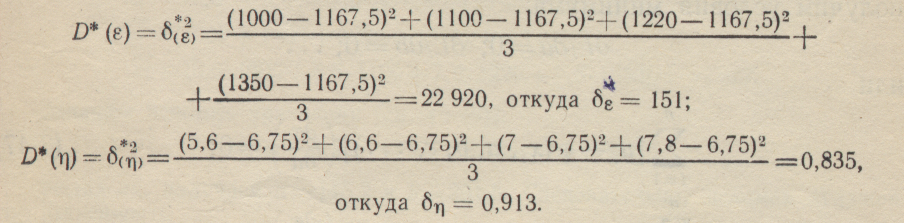
По формуле (1-46) определим величину статистического коэффициента кор­реляции;

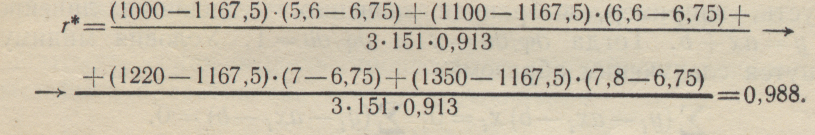
Запишем уравнение регрессии Р на W (т. е. ε на η):

M*w(P)=r*(δ*_ε/ δ_η)(W -- b) + а = 0,988(15l/0,913)(W-6,75) + 1167,5 = 67,5+163,2W. Зная ожидаемое значение W, можно определить м. о. величины Р.

При обработке экспериментальных и статистических материалов,

например, при определении коэффициентов корреляции, желательно избегать случайных ошибок измерения отдельных величин. Для этого экспериментальные зависимости одной случайной величины от другой случайной величины подвергают расчетному сглаживанию. Одним из методов расчетного сглаживания является метод наименьших квадратов.

Если известна экспериментальная зависимость у от x, то можно судить о характере зависимости (линейная, параболическая и т. д.) и выбрать формулу этой зависимости в одном каком-либо виде;

у = ах+b, |

или

у = ах²+bх+с, или

у == αx³ + bх² + сх + d, т. е.

y = φ(x,a,b,c,……)

где коэффициенты а, b, с, ... подлежат определению расчетным путем. Эти параметры выбираются так, чтобы сумма квадратов разностей фактически наблюденной величины у и той же величины, полученной по формуле у~·Ц1(х, а, Ь, с, ...), была наименьшей. Таким образом, критерий выбора величин а, Ь, с, ...

L= ∑[y_i - φ(x_i,a,b,c,…….)]² =min,

где у_i и х_i— полученные экспериментально значения.

Из правила определения минимума функции многих переменных

получим условия минимума:

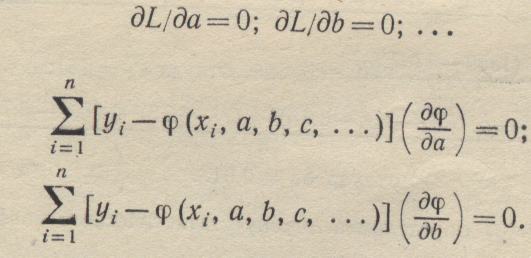(1·47)

(1-48)

Пусть, например, выбранная зависимость является линейной, т.е. у = ах + + в. Тогда dφ/da = x; dφ/db = 1. Условия минимума

запишутся следующим образом;

∑(y_i – ax_i – b)x_i = 0; ∑(y_i -- ax_i –b) = 0.

Если применить обозначения

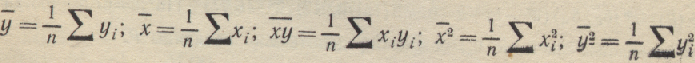
то условия минимума перепишутся:

откуда можно получить два уравнения для определения неизвестных параметров а и b:

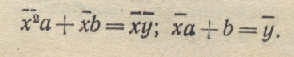(1-49)

Если выбранная зависимость параболическая, т. е.

у == φ (x) = αx'² + bх + с, то условия минимума запишутся тремя уравнениями:

Применяя аналогичные обозначения, можно получить три урав­нения для определения неизвестных параметров а, Ь и с:

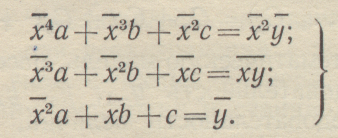
Пример 1-17. Полученную в примере 1-16 экспериментальную зависимость максимума энергосистемы Ρ от годовой выработки электроэнергии W будем сглаживать и виде линейной зависимости Р =аW + b, где Ρ = у.

Найдем искомые уравнения для определения a и b, для чего предварительно найдем следующие величины:

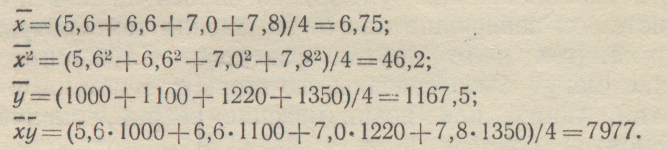
Запишем искомые уравнения [см. (1-49)]:

46,2а+6,75b =7977; 6,75а+b = 1167,5.

Решая их, получаем α =145,2 и b=201,5. Следовательно, искомая сглажен­ная зависимость

P=145,2W+201,5

1-5. Некоторые сведения о случайных процессах

Математическая модель процесса со случайными отклонениями может быть представлена в виде соотношения

x_i = φ(t) + ∆_I .

где x величины, отражающие ряд наблюдений (i=1,2, ..., n)

φ (t) -— некоторая детерминированная функция, отражающая общую тенденцию изменения x_i (иногда называется «детерминированная компонента» или «тренд»); Δ;—случайные отклонения, имеющие место при протекании процесса х_i. Эту величину можно рассматри­вать как появление ошибки по отношению к φ(t_i), благодаря чему процесс и становится случайным. Такой процесс иногда называется «тренд с ошибкой».

Предположим, что функция φ (t) задана некоторой формулой F (t, С₁, ..., С_к), в которую входят неизвестные параметры С₁ .. . С_к, выбранные так. чтобы φ (t) = F (t, C₁ ..., C_к). Для нахождения

С₁,..,С_к отыскивают min ∑ [x_i --F( t_i C₁..., С_к)]², т.е. ^ί=1

применяют метод наименьших квадратов. Если случайность рассматри­вать как основное свойство процесса, а не как отклонения от ос­новной тенденции изменения, то можно оперировать только со

случайными величина у₁,у_2…….,у_n, а не с детерминированными величинами х_i, при случайных к ним добавкам Δ_i.

Часто встречается случай, когда зависимость φ(t) неизвестна. При этом также используют соотношение φ(t) = F (t, С₁ ..., С_k,), однако функцию F выбирают произвольно. Часто представляют ее многочленом

φ(t) = (t, С₁,...., С_k) = С₁ + С₂t + С₃ t² +...+С_k t^k--!

Если расширить математическую модель, рассмотрев бесконечную в обе стороны последовательность у_-1, у₀, у₁,…..,у_n,y_n+1 , то можно получить последовательность величин, которая называется случайным процессом.

Случайные процессы в энергетике связаны, во-первых, с метео­рологическими условиями. К числу их можно отнести изменения располагаемой мощности и энергии гидростанций, зависящие от приточности рек; изменения суммарного спроса мощности и энергии в энергосистемах, зависящие как от изменения температуры наружного воздуха, так и от других факторов. Случайные процессы в энергетике могут быть связаны, во вторых, с потоками однород­ных событий, таких, как возникновение аварий, окончание ава­рийных ремонтов и т. п.

Вероятностные методы определения закономерностей, характе­ризующих случайные процессы в энергетике, пока только разраба­тываются; естественно, что методики использования их еще нет, если не считать применения метода Монте-Карло и теории массового обслуживания, рассматриваемых далее.

Определим количественные характеристики случайного процесса. Для каждого конкретного значения времени t случайный процесс характеризуется некоторой случайной величиной, которая назы­вается сечением случайного процесса. Если фиксируется определен­ное значение времени t, то случайный процесс превращается в слу­чайную величину (сечение случайного процесса); если фиксируется определенный конкретный опыт, то случайный процесс превращается в неслучайную функцию времени (реализация случайного процесса).

Случайный процесс представляет собой бесконечное множество случайных величин или бесконечное множество неслучайных функ­ций времени. Случайные величины, представляющие собой сечения случайного процесса, являются зависимыми величинами, т. е. имеют корреляционную связь. В этой связи и заключается единство процесса.

Естественно, что для случайного процесса невозможно найти общий закон распределения вероятности. Тем не менее, количест­венные характеристики случайного процесса можно получить на основании достаточно большого числа опытов, т. е. на основании статистической обработки большого числа реализации.

Обозначим величину, характеризующую случайный процесс, через Χ (t). Математическое ожидание случайного процесса M[Χ(t)]— это м.о. всех его сечений, в отличие от случайной величины яв­ляется не конкретной величиной, а конкретной функцией времени. Если обозначить м. о. сечения процесса для данного значения t через m (t), то очевидно, что

M [X(t) ] = m_x (t). (1-51)

Таким образом, искомая неслучайная функция времени M[Х(t)] может быть получена следующим образом. Для каждого значения времени путем статистической обработки наблюдении случайных значений находится конкретная величина m_x, равная м.о. случайной величины, которая наблюдалась при. данном значении t. Совокуп­ность значений m_x для всех значений t и определяет м. о, случай­ного процесса в виде функции времени. Аналогично могут быть определены значения дисперсии и стандартною отклонения:

D[X(t)] = D_x(t)·, (1-52) δ [Χ (t)] = δ_x (t). (1-53)

Обе эти величины являются также неслучайными функциями времени и определяются для каждого момента времени сечения на основании обработки наблюдений за значениями случайной вели­чины, в которую превращается процесс при конкретном значении t.

Значений м. о. и дисперсии случайного процесса недостаточно для его полной характеристики, так как отдельные сечения процесса имеют корреляционные связи, т. е. не являются независимыми слу­чайными величинами. Для полной характеристики случайного про­цесса нужно знать еще одну величину—так называемую корреля­ционную функцию процесса, которая представляет собой м.о. произ­ведения центрированных значений двух случайных величии для двух произвольных конкретных значений времении t и t'. Обозначая корреляционную функцию для моментов времени t и t' через Κ_x (t , t'), из определения получим

К _x (t ,t’) = M [ X”(t) X”(t’)] (1 – 54)

где центрированное значение Χ” (t) равно разности случайной функ­ции времени и ее м.о.:

X”(t) = X(t) – m_x (t). (1-55)

У близких по времени сечений корреляционная связь обычно

сильная и величина Κ_x{t, t'} может быть значительной.

Если t' = t, то корреляционная функция превращается в диспер­сию для данного сечения:

K_x (t , t) = M[X (t )]² = D_x(t). (1-56)

Если использовать понятие нормированной случайной величины

X_N(t) = [X(t) – m_x (t)] / δ_x (t) = X(t) / δ_x(t), (1-57)

то очевидно, что м. о. произведения двух нормированных сечений равно коэффициенту корреляции этих сечений:

ρ_x (t,t’ ) = K_x (t,t’) / [ δ_x (t)δ_x (t’)] = M[ X_N(t) X_N (t’)]. (1-58)

При t = t’ этот коэффициент

ρ_x (t,t) = D_x (t) / δ_x² (t) = l. (1-59)

Пусть имеется n реализаций некоторого случайного процесса, причем n достаточно велико. Найти основные количественные харак­теристики случайного процесса: м. о. m_x (t) , дисперсию Dx(t), коэф­фициенты корреляции ρ_x (t ,t').

Для этого выбирают ряд сечений процесса, соответствующих дискретным значениями времени t₁ ,t₂ ,……t_m .

Обычно это сечения, равноотстоящие по времени. Однако иногда уменьшают интервалы между сечениями в определенных промежут­ках времени для более тщательного изучения закономерностей случайного процесса в данной области. Составляют таблицу значе­ний наблюденной случайной функции времени Χ(t).

x(t)	Значения зафиксированной случайной функции времени
	t1	t2	t3			tm
x1(t) x2(t) x3(t)	x1 (t1) x2 (t1) x3 (t1)	x1(t2) x2 (t2)	x1(t3) x3(t3)	··		x1(tm)
…. xn(t)	……. xn(t1)	……	……	…

В этой таблице каждая строка соответствует конкретному опыту, т.е. какой-нибудь реализации процесса; каждый столбец—конкрет­ному значению времени, т. е. какому-нибудь сечению процесса. Тогда м. о. для сечения t_k

_n

m_x (t_k ) = ∑ x _i (t_k ) / n (1-60)

_{i = 1}

Дисперсия для сечения t_k

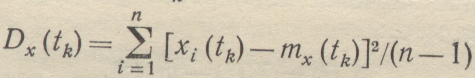(1-61)

Корреляционный коэффициент для сечений t_k и t_l

(1-62)

По формулам (1-60) и (1-61) строят зависимости m_x(t) и D_x(t) по точкам.

Значения ρ_x (t, t') получают в виде таблицы, где число строк и столбцов равно m и соответствует моментам времени t₁,t₂ ,…..

В каждой клетке для строки t_k и столбца t_l помещают вычисленное значение ρ_x Полученные числовые значения характеризуют данный случайный процесс. Таким способом могут быть обработаны статистические данные по спросу мощности, пока­затели изменения приточности рек, определяющие располагаемые мощности и энергию гидростанций, данные но изменению темпера­туры наружного воздуха, влияющие на спрос мощности бытовыми потребителями, и т. п

.

Пример 1-18. Пусть в энергосистеме и течение пяти суток наблюдались сле­дующие мощности спроса (в 1000 МВт) за характерные часы суток 4, 10, 16, 19 и 24,

Часы суток	Мощность спроса за сутки
	первые	вторые	третьи	четвертые	пятые
4	5	6	4	6	5
10	12	11	10	13	11
16	9	8	8	10	8
19 ·	18	17	17	19	18
24	10	9	8	11	11

Рассматривая спрос как случайный процесс, можно найти м. о., дисперсии, стандартные отклонения и корреляционные коэффициенты для указанных сече­ний процесса и на основе этих данных предсказать спрос в 19ч, если в 10 ч утра наблюдался спрос в 12000 МВт.

Определим м. о. сечений по (1-60);

М₁ = (5+6+4+6+5)/5 = 5,2; М ₂ = (12+11+10+13+11)/ 5 = 11,4;

М₃ = (9+8+8+10+8) /5 = 8,6; М₄ = ( 18 + 17+17+19+18) /5 =17,8;

М₅ = (10+ 9+8+11+11) / 5 =9,8.

М,

Вычислим дисперсии по (1-61) и стандартные отклонения

D₁ = (5-5.2)²ⁱ+(6-5,2)²+(4--5,2)²+(6—5,2)²+(5—5.2)² / 4 =0,7; δ₁= 0,837;

D₂ = 1.3: δ₂ = 1,14;

Dз=0,8; δ₃=0,895;

D₄ = 0.7; δ₄ =0,837;

D₅ = 1.7; δ₅ = 1,31.

Найдём коэффициенты корреляции по (1-62):

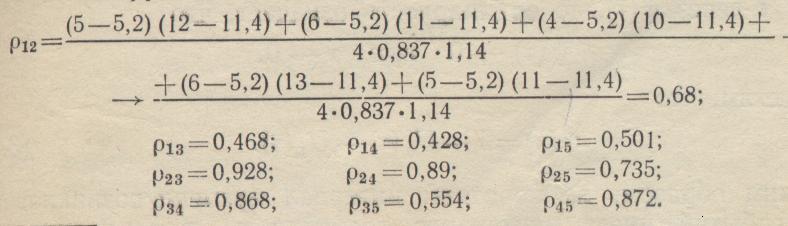
Как видно, наиболее сильная корреляционная зависимость имеет место

между спросом в 10 и 14, 10 и 19, 14 и 19, 19 и 24 ч.

Если в 10 ч утра спрос был 12 тыс. МВт, то по (1-45) найдем м. о. спроса в 19 ч:

M_{P 10} (P₁₉) = ρ₂₄ (δ₄ / δ₂) (Ι2-1Ϊ,4)+ 17,8= ' =0,89(0,837/1,14)0,6+17,8=0,39+17,8=18,19 тыс. МВт.