Условной вероятностью события а по в называется вероятность события а, если происходит событие в. Она обозначается через р{а/в}.

Основные законы для взаимозависимых случайных событий фор­мулируются следующим образом :

1) условная вероятность события А по В при их совместимости и взаимозависимости равна отношению вероятности одновременного наступления событий А и В к вероятности события В:

Р{А/В}==Р(АВ)/Р(В}, (1-7)

причем Р(АВ) в этом случае не равно Ρ (Α}· Ρ {В};

2) вероятность одновременного наступления двух взаимозависимых и совместимых событий, как это следует из (1-7), равна произ­ведению условной вероятности первого события по второму на ве­роятность второго события:

Ρ (АВ) = Ρ (А/В) Ρ (В). (1-8)

Взаимозависимыми событиями в энергетике являются, например,

повреждения отдельных фаз линии передачи. При повреждении одной фазы линии передачи в сети с незаземленной нейтралью на­пряжения других фаз возрастают в √3 раз, что увеличивает веро­ятность повреждения других фаз. Но даже в сети с заземленной нейтралью, где повышение напряжения на других фазах не проис­ходит, ионизация воздуха, обусловленная коротким замыканием на одной фазе, способствует перекрытию других фаз. Если исходное повреждение одной фазы является независимым случайным собы­тием, то одновременное повреждение фаз в том же месте является зависимым случайным событием.

Пример 1-3. Пусть статистическая вероятность повреждения любой фазы линии составляет 0,001. Примем также, что если повреждение одной фазы про­изошло. го повреждение любой другой фазы будет иметь статистическую вероятность 0.2, т. е. условная вероятность повреждения второй фазы при повреждении первой равна 0,2. Кроме того, пусть аналогичные вероятности повреждения третьей фазы при повреждении двух других составляют 0,5. Определим соотношения вероятностей одно-, двух- и трехфазных коротких замыканий при условии, что авария началась с повреждения одной фазы.

Вероятность аварийного повреждения двух фаз [см. (1-8)] p’=0,2.0,001 =0,0002.

Вероятность аварийного повреждения трех фаз р"==0,5·0,0002=0,0001.

Определим условные вероятности развития аварии, т. е. условные вероят­ности повреждения других фаз. Пусть статистические наблюдения установили, что однофазных коротких замыканий в данной сети за некоторый длительный период времени было 100, а в 20 случаях из них повредилась и другая фаза. Тогда на основании формулы (1-7) можно получить условную вероятность по­вреждения и другой фазы;

Р(А/5)==Р(АВ)/Р(В)=20/100==0,2,

так как число аварий можно считать пропорциональным вероятности.

Таким образом, соотношения вероятностей одно-, двух- и трехфазных повреж­дений будут: 0,001; 0,0002; 0,0001 или примерно 77% однофазных, 15% двух­фазных и 8% трехфазных.

При большом числе однотипных агрегатов в электрической системе вероятности повреждения различного числа агрегатов могут быть определены по биноминальной формуле вероятности для схемы не­зависимых испытаний (схема Бернулли).

Во многих практических случаях при многократных независимых испытаниях могут быть только два исхода: случайное событие А произойдет или не произойдет. Пусть вероятность того, что в каж­дом из этих независимых испытаний событие А произойдет, равна р, где р— статистическая вероятность. Тогда вероятность противопо­ложного события (событие А не происходит)

q = 1 – p.

Зная р или q, можно определить вероятность того, что в n не­зависимых испытаниях событие А, например повреждение агрегата, случится m раз. Обозначим эту вероятность через Р^m_n. Она_равна, произведению числа комбинаций из n по т на вероятность события в степени т и на противоположную вероятность в степени {п—т):

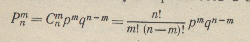(1-9)

Выражение (1-9) называют формулой биноми­нального распределения. Очевидно, что

(1-10)

так как эта сумма охватывает все возможные события (т варьиру­ется от 0 до n).

Формулу (1-9) можно получить также, рассуждая следующим образом. Рассмотрим выражение (q + p)^m Оно, очевидно, равно еди­нице, так как (q +p) = 1. Разлагая п-ю степень бинома (q+р) в ряд по известному закону, получим

(1-11)

Нетрудно понять смысл членов разложения. Первый член qⁿ соответствует вероятности того, что в n испытаниях событие А не произойдет ни разу, т. е. равен Р⁰; второй член—вероятности того, что в n испытаниях событие А произойдет только один раз; т. е. равен P¹_n.Действительно, вероятность того, что событие произойдет при каком-то одном определенном испытании, будет pq ^n--1 , а веро­ятность того, что событие произойдет при каком-то любом одном испытании, в n раз больше и т. п. Член разложения (m+1)-й, соответствующий вероятности того, что событие происходит т раз, равен C^m_n q^n-m p^m , т.е. Р^m_n [см. (1-9)].

Вместо различных испытаний рассмотрим различные однотипные агрегаты, предполагая, что вероятность аварийного состояния для каждого из агрегатов одинакова и равна q.

Пример 1-4. Пусть р, энергосистеме имеется группа из п однотипных агрега­тов (например, котлов или турбин), находящихся в совершенно одинаковых ус­ловиях; вероятность исправного состояния агрегата равна р, а вероятность

противоположного события, т. е. неисправного состояния агрегата (аварийного ре­монта), равна q . Найдем вероятность рабочего состояния m агрегатов из числа n,

причем т изменяется от 0 до п·

Нетрудно убедиться в том. что разложение по (1-11) определяет искомый ряд вероятностей. В самом деле, qⁿ—это. очевидно, вероятность того, что все агре­гаты повреждены и число работоспособных агрегатов равно нулю; npq^n--1—ве­роятность того, что только один агрегат находится в рабочем состоянии;

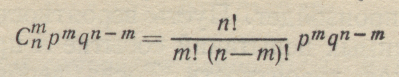
—вероятность рабочего состояния т агрегатов; pⁿ—вероятность того, что все агрегаты находятся в исправном.и состоянии.

Если определять вероятность не рабочего состояния, а аварийного повреж­дения различного числа агрегатов, то целесообразно записать тот же ряд в сле­дующем порядке:

(1-11а)

где( m + 1)·й член определяет вероятность выхода из работы т агрегатов, рав­ную

C^m_n p^{n – m} q^m.

Если, например, п=5, р==0,98 и q=0,02, то вероятность отсутствия ава­рийных выходов

рⁿ = 0 ,98⁵ = 0,905. Вероятность аварии с одним агрегатом

и т. д.

Пример 3-5. Определим вероятность выхода из строя какого-либо количества агрегатов в -энергосистеме. Если в системе имеется пять групп однотипных агре­гатов с числом агрегатов n₁ – n₅ и вероятностями повреждения агрегатов q₁ – q_5, тο вероятности любых комбинаций одновременных повреждении агрегатов можно найти из разложения выражения

Так, например, вероятность аварийного выхода двух агрегатов 1-й группы, одного агрегата 3-й группы и одного агрегата 5-й группы равна

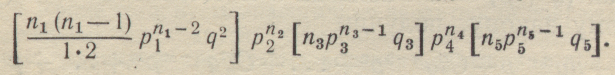
1-3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

К случайным величинам в энергетике относятся такие важные

параметры режима, атокак спрос электрической мощности и энергии, отклонения частоты и напряжения в электрических сетях от номи­нальных значений, располагаемая мощность электростанций, мощ­ность агрегатов в аварийном ремонте, длительности безаварийной работы и аварийного ремонта отдельных агрегатов, напор на гидро­станциях и т. д. Знание закономерностей изменения этих случай­ных величин необходимо как при проектировании, так и при экс­плуатации энергетических систем. Основой для их изучения является статистический материал и методы теории вероятности.

Прежде чем рассматривать случайные величины в энергетике, остановимся на

методах описания их закономерностей. Случайные величины можно разделить на два класса: дискретные и непрерыв­ные. Дискретная случайная величина может принимать только дискретные значения, например число агрегатов, вы­шедших аварийно из работы. Это число в ограниченном интервале является конечным. Значения непрерывных случайных величин могут изменяться непрерывно, т. е. даже в ограниченных интервалах такие величины могут иметь бесконечно большое число значении, напри­мер -- ошибка прогнозирования суммарного спроса мощности. Для дискретных случайных величин распределение вероятностей различ­ных их значений может быть наиболее просто задано с помощью таблиц распределения, в которых в верхней строке указываются все значения, принимаемые данной дискретной случайной величиной, а в нижней — вероятности соответствующих ей значений. Очевидно, что сумма вероятностей должна равняться единице, если данная случайная величина всегда принимает одно из возможных значений.