Раздел 3 математический аппарат для изучения переходных процессов с учетом нелинейностей

3-1. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОГО процесса С ПОМОЩЬЮ ЧИСЛЕННЫХ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

При исследовании переходных процессов

в электрических системах необходимо решать системы обыкновен­ных дифференциальных уравнений. В большинстве случаев эти уравнения не линейны и их нельзя решить в общем виде. Иногда по условиям задачи может быть выбрана линейная модель, однако ее порядок высок, тогда более эффективными оказываются числен­ные методы решения. Отметим, что численное интегрирование — наиболее общий метод исследования переходных электромеханиче­ских процессов в электрических системах, особенно с учетом не­линейностей.

Прежде чем говорить о некоторых наиболее распространенных методах численного решения численного дифференциальных уравнений, рассмотрим первого порядка их общий подход на примере уравнения первого порядка

x^′ = f (t, x ) (3-1)

Рассмотрение одного уравнения первого порядка не уменьшает общности получения результатов, так как все методы численного решения, применимые для уравнения (3-1). обобщаются для систем уравнений первого порядка, а уравнение n-го порядка можно свести к п уравнениям первого порядка. Пусть имеется уравнение второго порядка

x״ + ax′ = t².

Оно эквивалентно системе двух уравнений первого порядка :

x′ = y; y′ = t²– ay.

Как известно, общим решением уравнения (3-1) называется ре­шение, зависящее от произвольной постоянной интегрирования и содержащее все частные решения исходного уравнения. Очевидно, что подобное решение получить численными методами нельзя. Они используются для нахождения частного решения уравнения, удов­летворяющего заданным начальным условиям:

t = t_0, x(t₀) = x_{0 .} (3-2)

Заменим в уравнении (3-1) производную х' отношением конеч­ных малых приращений Δх и Δt:

Δx/Δt=f{t, x),

откуда

Δ x = f{t, х)Δt (3-3)

Зная начальные условия интегрирования согласно (7-3), запи­шем приращение искомой функции на первом шаге в следующем виде:

Δx₁ = f (t₀ , x₀) Δt, т.е. x₁ = x₀ + Δx₁.

Аналогично получим приращения искомой функции на втором шаге, зная значение правой части уравнения (3-1) при t=t₁ и x = x₁

Отмечая нижним индексом «k-» значения переменных на k-м шаге интегрирования, представим (3-3) как

Δx_k+1 = f (t_k , x_k ) Δt (3-4) или

Δx_{k + 1} = x_k + f ( t_k , x _k ) h (3-5)

где Δ t = h -- шаг интегрирования.

Рассмотрим геометрический смысл выражения (3-4),

зная, что

для производной—это тангенс угла наклона касательной L к интег­ральной кривой х (t) в заданной точке (t _k , x _k ) по отношению к оси абсцисс (рис. 3-1). Метод численного решения дифференциального уравнения сводится к замене реальной интегральной кривой конеч­ным числом прямолинейных отрезков. При этом возникают ошибки двух видов: ошибка ограничения (локальная ошибка интегрирова­ния, показана на рис. 3-1 отрезком e) и накапливаемая (интеграль­ная) за время интегрирования ошибка. Наличие этих ошибок может приводить в некоторых случаях к совершенно неприемлемым результатам. Для их уменьшения есть только один путь—уменьшение шага интегрирования, что при неизменном полном времени

интегрирования ведет к удлинению счета. Таким образом, при не­обходимости получения более точного результата при том же шаге следует использовать другие, более точные методы интегрирования. Решение с помощью рядов Тейлора, Если функция х {t} в окрестности точки i достаточное число раз дифференцируема, то для нахождения ее значения при t+h можно воспользоваться разложени­ем Тейлора

n

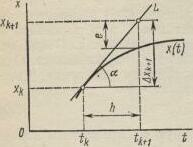Рис.3-1

Δx = x(t + h) – x(t) = ∑(x^(m)/ m!) h ^m + 0(hⁿ⁺¹), (3-6)

где все производные вычислены в исход- ной точке; O(h⁽ⁿ⁺¹⁾)означает, что в следующие члены ряда величина h входит в степени не ниже n+1 ,

т. е. ошибка ограничения в пер­вом приближении равна, Кhⁿ⁺¹, где K -- некоторая константа.

Данный метод теоретически пригоден для решения любых диф­ференциальных уравнений, однако при его практическом использо­вании встречаются довольно серьезные трудности. Они обусловлены тем, что при нахождении высших производных функций х в случае нелинейной правой части уравнения (7-1), выражения .для произ­водных все время усложняются по мере роста порядка производ­ной. Действительно, уже для второй производной имеем

x"=df(t, x)/dt+f{t, x)df(t, х)/дх.

Однако данный метод может служить эталоном при при сравнении с другими методами интегрирования поскольку все они в той или иной степени согласуются с разложением Тейлора. Так, например, метод, описанный выше и известный в литературе как метод Эйлера, является методом первого порядка, в котором выражение (3-5) согласуется с разложением Тейлора до членов с первой степенью h , т.е. в первом приближении ошибка ограничения этого метода равна Kh² .

Таким образом, каждый метод интегрирования характеризуется порядком, хотя это не единственная характеристика метода. По­скольку все методы в той или иной степени согласуются с разло­жением Тейлора, то в методах, порядок которых выше единицы, высшие производные разложения (5-6) находятся косвенным обра­зом. При этом возможны два подхода. Первый—нахождение про­межуточных значений правой части уравнения (5-1) на интервале (t_k, t_k + h ) , а второй—использование значений функции х на пре­дыдущих шагах интегрирования. В случае метода п-го порядка при первом подходе необходимо n раз пересчитать правую часть уравнения (5-1), при втором—для определения x_k+1 дополнитель­ных пересчетов правой части уравнения делать не требуется и это обстоятельство является крайне благоприятным, так как умень-

шается продолжительность счета. Однако с помощью методов, по­рядок которых выше единицы, невозможно начать интегри­рование, поскольку они не содержат предшествующей информа­ции о ходе решения уравнения.

'Таким образом, все методы дополнительно можно классифици­ровать на одношаговые (самоиачинающие) и многошаго­вые, не дающие возможность начать решение.

Рассмотрим методы, наиболее широко используемые при ре­шении практических задач.

Методы Рунге — Кутта. Эти методы обладают

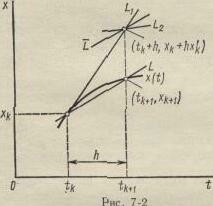
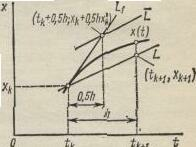
Рис. 3-2 Рис. 3-3

следующими свойствами:

1)являются одношаговыми;

2) согласуются с разложением Тейлора до членов порядка h^p, где p имеет различное значение для каждого метода и называется его порядком;

3) не требует вычисления производных от f( t, x).

можно трактовать как метод Рунге – Кутта первого порядка.

Причина значительных погрешностей метода Эйлера заключается в том, что для экстраполирования искомой функции на шаге интегрирования используется наклон касательной только в точке (t_k,x_k).

В методах Рунге—Кутта второго порядка для экстраполяции используется определенным образом усредненный наклон касатель­ных на шаге интегрирования. Методы Рунге—Кутта описываются формулой вида

x_k+1 = x_k + h Ф ( t _k, x_k , h). (3-7)

Усреднить тангенс наклона касательной на шаге интегрирования

можно следующим образом (рис. 3-2). С помощью метода Эйлера находится точка (t _k + h, x_k + hx^′_k), лежащая на прямой L₁. В этой точке вновь вычисляется тангенс угла наклона касательной (пря­мая L₂). Усреднение тангенсов дает прямую L. Через точку (t_k , x_k) проводится прямая L, параллельная L, и находится искомая точка (t_k+1 , x_k+1 ).

В этом случае, очевидно, функция Ф [см. (3-7)] запишется как

Ф = 0,5[ f(t_{k ,} x_k ) + f( t_k + h, x_k + hx^′_k )], (3-8)

где x'k==f(tk. Xk)-

Можно поступить иначе, определив тангенс наклона касатель­ной в средней точке интервала экстраполяции (шага интегрирова­ния), как это показано на рис. 7-3. В этом случае

Ф = f(t_k + 0,5 h, x_k + 0,5hx^′_k ). (3-9)

Без вывода приведем формулы, описывающие метод четвертого порядка, один из самых употребительных методов интегрирования дифференциальных уравнений. Этот метод применяется настолько широко, что в литературе по вычислениям на ЦВМ он называется «метод Рунге—Кутта» без всяких указаний на тип или порядок. Этот классический метод Рунге—Кутта описывается системой сле­дующих соотношений:

x_k+1 = x_k + h(k₁ + 2k₂ +2k₃ +k₄)/ 6,

где

k₁ = f ( t _k , x _k ); k₂ = f ( t_k + 0,5 h, x_k + 0,5 h k₁ ); k₃ = f(t_k + 0,5hk₂);

k₄ = f(t_k + h, x_k + hk₃).

Данный метод самоначинающий, но один из его недостатков—

сложность оценки локальной ошибки интегрирования -является об­щим недостатком всех методов Рунге —Кутта. Поэтому при реализации метода с автоматическим выбором шага интегрирования поступают следующим образом. Вычисляют значение искомой функции в каж­дой точке с полным и с половинным шагом и сравнивают два по­лученных значения. Если модуль разности между ними окажется меньше некоторого заданного положительного числа, то считается, что интегрировать с данным шагом можно; если же это не так, то шаг делится пополам. Этот метод выбора шага интегрирования при­водит к увеличению времени счета как минимум в три раза по сравнению с методом постоянного шага.

Некоторые особенности анализа переходных процессов в элект­рической системе. Рассмотрим особенности анализа переходных про­цессов в электрической системе с точки зрения метода решения за­дачи:

1) численное интегрирование дифференциальных уравнении при­меняется, как пронзило, при анализе динамической устойчивости системы после короткою замыкания на линии электропередачи или после наброса нагрузки на генераторы системы. При этом в моменты возникновения коротких замыкании и их отключении ряд режим­ных параметров терпит разрывы первого рода, что приводит к скач­кам производных. При использовании многошаговых методов даль­ней шее интегрирование с использованием предшествующей инфор­мации невозможно, т. е. возникает ситуация, подобная начальному этапу интегрирования, а многошаговые методы не являются само­начинающими;

2) порядок системы уравнений, описывающих поведение слож­ной электрической системы, высок, что, с одной стороны, приводит к естественному увеличению времени счета, а с другой,—к столь же естественному увеличению объема оперативной памяти ЦВМ, нани­маемого программой;

3) переходные процессы в элементах электрической системы раз­личаются но времени протекания (электромеханические, электро­магнитные и т, д.), а также по интенсивности изменения режимных параметров, связанной с тем, насколько близок, например, генера­тор или группа генераторов системы к точке короткого замыкания. Это обстоятельство при численном решении задачи можно было бы использовать с целью сокращения времени счета, выбирая раздельные шаги интегрирования для различных групп уравнений системы.

Таким образом, наиболее целесообразным был бы самоначинающий, быстродействующий_и легко программирующийся метод, поз­воляющий легко оцепить локальную ошибку интегрирования для каждой интегрируемой переменной и независимо выбрать для них шаг интегрирования.

Метод последовательных интегралов. При исследовании динами­ческой устойчивости электрических систем применяется простой метод интегрирования дифференциальных уравнений, дающий удовлетворительную точность решения.

Пусть необходимо проинтегрировать систему дифференциальных уравнений следующего вида:

T_{J I} d²δ_i/dt² = P_{T i} -- P_Эi , (5—10) где

Рэ_i = y_ii E²_i sin α_ii -- ∑ y_imE_i E_m sin (δ_i –δ_m –α_im), i=l, 2, ..., η.

От системы n уравнений второго порядка (7-10) можно перейти к системе 2п уравнении первого порядка

dδ / dt = ω_i ; T_J dω/ dt = P_Ti -- P_Эi. (5-11)

Предположим, что в системе происходит короткое замыкание. Тогда, если в исходном режиме δ_i = δ_{i 0} , ω = 0 , ΔP = 0 для каж­дого генератора, то после короткого замыкания ΔР не равно О. При этом изменяются и значения проводимостей схемы, а следовательно, и значения Рэ и ΔР==Рг—,Рэ . Обозначая ускорение ротора i-го генератора через α=ΔP/Τ_J и считая его постоянным, запишем приращение угла генератора ηа первом шаге интегрирования h

Δδ_i.= 0,5α₀h².

Применяя для каждого генератора формулу δι=δο+Δδι, найдем значения углов δ к началу второго шага интегрирования. Очевидно, что ко второму шагу интегрирования ω не равна нулю. Прираще­ние ω на первом шаге интегрирования определим по среднему ускорению генератора, т. е. по формуле

Δω₁ == 0,5h (α₁+ α₀),

где α = ΔP₁ / T_J..

k-ι

••Σ

s=l

Для второго интервала

Δδ = Δω₁h + 0,5 α₁h².

Таким образом, интегрирование для всех последующих интервалов производится по формулам:

ω_k = ω_k—1 + 0,5h (α_k + α_k—1); (3—12)

δ_k+1 = δ_k + ω_k h + 0,5α_k h², ( 3—13)

т.е. это метод второго порядка, однако в отличие от метода Рунге – Кутта того же порядка, не требуется дважды пересчитывать правые части исходной системы уравнений при определении приращений искомых переменных на шаге интегрирования.

Последние выражения можно преобразовать к более удобному для вычислений виду:

ω_k = h/2∑(α_S + α_S—1) = 0,5α_kh + h∑ α_s + 0,5 α₀h;

δ_k+1 = δ_k + h² ∑α_s + 0,5α₀ h². (5—14)

Очевидно, что

δ_k = δ_k---1 + Δδ_k = δ_k—1 + h²∑ α_s + 0,5α₀h²,

и Δδ_k = h² ∑α_s + 0,5α₀ h²

Следовательно, (5-14 ) можно переписать:

δ_{k +1}= δ_k + Δδ_k + α_kh².

Δδ_{k+ 1} = Δδ_k+ α_kh^{2 ;}

δ_k+1= δ_k + Δδ_k+1;

α_k = 18000ΔP_k/T_J,

где углы δ измеряются в электрических градусах, время интегри­рования и постоянная инерции T_J—в секундах, небаланс мощно­сти Δρ—в относительных единицах. Алгоритм метода следующий;

1/Установить m = 1 2/ Определить константу k = (18000/Tj} h².

3.ВычислитьΔΡ₀=Рт-Рэ (Пункты 1 – 5 выполняются однократно)

вы-одно-

4. Определить Δδ₁==0,5kΔΡο.

кратно

5. Найти δ₁=δ₀ + Δδ₁

6. Вычислить ΔР_m=Р_T—Рэ .

7. Определить Δδ_{m+ 1}=Δδ_m +kΔP_m.

8. Найти δ_m+1 = δ_m+ δ_m+ Δδ_m+1.

9. Увеличить m на единицу {m—>m+ 1}.

10. Если mh не больше заданного времени интегрирования, то перейти к п. 6, если mh больше, то счет оканчивается.

Данный алгоритм справедлив как во время короткого замыкания, так и после его ликвидации. Однако непосредственно в момент отключения ускорение α претерпевает разрыв первого рода, по­этому п. 6 алгоритма для моментов коммутаций следует изменить и определить небаланс мощности по формуле

ΔΡ_m=0,5(ΔΡ_{m +} +ΔΡ_M-),

где индекс «+» свидетельствует о том, что ΔΡ необходимо вычислить при послеаварийных значениях проводимостей у, а «_» о том, что значения проводимостей отвечают аварийному состоянию в системе (короткое замыкание).

Данный метод можно использовать и в тех случаях, когда ис­следуется устойчивость регулируемой системы с учетом изменения ЭДС генераторов. Однако в этом случае он уже не является мето­дом второго порядка, так как «новые» значения ЭДС определяются по формуле Эйлера.

Среднеиитервальный метод. Этот метод относится к методам про­гноза и коррекции первого порядка. Вообще говоря, методы про­гноза и коррекции не являются самоначииающими, за исключением методов первого порядка, поэтому данным методом можно начать решение.

Для прогноза в данном методе используется формула Эйлера

x_k+₁ = x_k + hf ( t_k ,x_k),

с помощью которой грубо экстраполируется значение искомой функ­ции на шаге интегрирования. Локальная ошибка данного метода велика и задача состоит в том, чтобы скорректировать ее, Для коррекции используется следующая формула второго порядка (за­метим, что в ней верхние индексы указывают на порядок итера­ционного приближения решения, а нижние—на интервал интегри­рования):

x^(m+1)_k+1 = x_k+ 0,5h[ f(t_k,x_k ) + x′_{k +1}], (3-15)

где x′_k+1 = f( t _k + h, x^m_k+1).

Данный метод имеет сходство с методом Рунге—Кутта второго порядка. Однако при использовании метода Рунге—Кутта формула (5-15) применяется во всех случаях один раз, а при использовании данного метода корректировка проводится до тех пор, пока не вы­полнится условие

[ x^m+1_k+1 -- x^m_k+1 ] ‹ έ (3-16)

где ε—заданная положительная величина.

В данном методе в зависимости от того, сколько итераций не­обходимо сделать для выполнения условия (5-16), можно выбирать шаг интегрирования: если этих итераций много—шаг следует умень­шить, если итерация одна, то шаг можно увеличить.

3-2. ПОНЯТИЯ КАЧЕСТВЕННЫХ ХАРАКТЕРИСТИК ДЛЯ ВОЗМОЖНЫХ ВИДОВ ДВИЖЕНИЯ НЕЛИНЕЙНОЙ СИСТЕМЫ

Несмотря на широкое применение компъюторов, расширяющее возмож­ности построения переходных процессов с помощью численных ме­тодов, актуальным является использование простых, приближенных методов исследования нелинейных дифференциальных уравнений. Приближенные методы особенно ценны, когда они приводят к ана­литической форме решения, позволяющей получить важные практи­ческие рекомендации более общего характера, имеющие силу не только для данной конкретной системы, но и для целого класса аналогич­ных систем. Приближенная оценка основных динамических свойств нелинейной системы позволяет наметить пути последующего приме­нения вычислительных машин. Эти соображения являются особенно важными при исследовании нелинейных дифференциальных уравнений, описываю­щих электрическую систему.

Характерные особенности регулируемой электрической системы— возможность существования нескольких состоянии равновесия, на­личие разных видов движения и, в частности, периодических дви­жений—устойчивых и неустойчивых предельных циклов. Дадим наглядную иллюстрацию на фазовой плоскости (в координатах откло­нения и первой производной переменной) качественных особенностей возможных видов движений в нелинейной электрической системе.

Рассмотрим понятие фазовой плоскости для системы, движение которой описывается уравнением второго порядка

d^2.x./ dt² + ω₀² x = 0. (3-17)

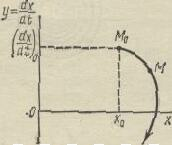
Состояние системы в данный момент времени t₀ определяется двумя координатами:

(x)_{t = t0} = x₀ ; (dx/dt) _{t =t0} = (dx/dt)_0.

Примем величины x и y = dx/dt в качестве декартовых коорди­нат на плоскости (рис. 3-4). Точка .М на плоскости, имеющая координаты x₀ и (dx/dt)₀ будет соответствовать некоторому состоя­нию системы, движение которой описывается уравнением (5-17). Точка М, положение которой полностью характеризуется состоя­нием системы, называется изображающей точкой, а плоскость (.x , dx/dt} — фазовой плоскостью. При движении системы ее состоя­ние изменяется и изображающая точка М, находящаяся в началь­ный момент времени t==t₀ в положении М₀, описывает некоторую кривую (см. рис. 5-4), которая называется траекторией изобра­жающей точки на фазовой плоскости. Запишем решение уравнения (3-17)

x = A sin (ω₀ t + φ) . (3-18)

Здесь А и φ—постоянные, определяемые из начальных условий.

Дифференцируя выражение (3-18), находим

у = dx/dt = Αώ_o cos (ω_o t + φ). (3-19)

Исключая величину ω_ot +φ из (3-18) и (3-19), получаем урав­нение

x²/A² + y²/ (A²ω_o² ) = 1,

представляющее собой уравнение эллипса с полуосями A и ω_o Α.

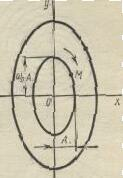
Итак, если система находится в движении, описываемом урав­нением (5-17), то изображающая точка движется по эллипсу (рис. 5-5). При этом время нигде не отображено на фазовой плоскости и можно лишь представить себе, что с течением времени изображающая точка Μ будет двигаться по траектории в направлении, указанном стрелкой. При других начальных условиях частное решение урав­нения (5-17) дает другую траекторию, например траекторию, на которой находится точка N.

Две траектории не могут пересечься, так как после пересечения последующее движение становится неоднозначно определенным. Между тем любая реальная система при определенных заданиях

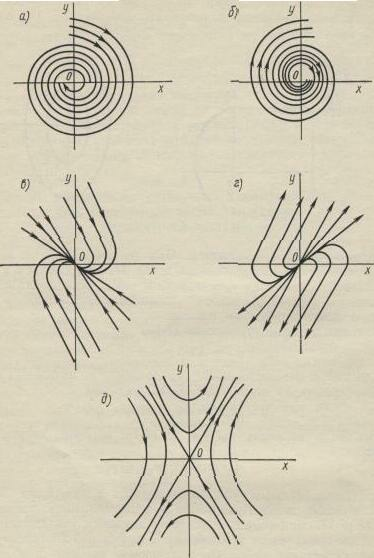
Рис. 3-6

начальных условий имеет лишь одно определенное движение, а не 'два или более «возможных» движений. Исключение составляют особые точки на фазовой плоскости, соответствующие состояниям равновесия системы. В нелинейной системе может быть несколько состояний равновесия.

Так, в нелинейной системе, описываемой уравнением второго порядка

d²x/dt² + 2βdx/dt + ω_o² sin x = ω_o² sin x_o,

может быть два состояния равновесия, определяемые как sinx= sin x_o,

где х==x_o и х=л – x_o.

Первое состояние равновесия (2β)² < ω_о ² называется устойчивым

фокусом (рис. 3-6, а).

Второе неустойчивое состояние равновесия называется седлом (рис. 3-6. д). На рис. 3-6, б, в, г приведены и другие возможные

a

Рис. 3-7

особые точки- неустойчивый фокус, устойчивый узел и неустойчи­вый узел соответственно.

Исследуя характер движения нелинейной системы на фазовой плоскости для распознания всей картины траекторий, т. е. так на­зываемый фазовый портрет системы, необходимо уделить особое внимание особым траекториям. Заметим, что точки равновесия являются частными случаями особых траекторий.

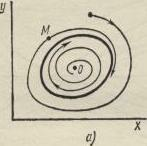
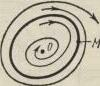
Периодические движения, при которых через каждый период времени Т исходное состояние системы повторяется, представляются замкнутыми фазовыми траекториями. В консервативных системах кривые, соседние с периодической кривой, обычно также пери­одические. Характерной картиной при существовании периоди­ческих движений в консервативной системе является совокупность замкнутых траекторий, «вложенных» одна в другую (см. рис. 3-5). Нет никаких оснований назвать какую-либо из этих траекторий особой. Однако в неконсервативных системах замкнутые траектории имеют принципиально другое значсние. Здесь существуют только изолированные замкнутые траектории, представляющие собой осо­бые траектории, называемые предельным циклом.

На рис. 3-7, а, б приведены примеры устойчивого и неустой­чивого предельных циклов. Начальная точка М, лежащая в области,

окружающей устойчивый предельный цикл (внутри или снаружи его), с течением времени переходит на траекторию предельного цикла, и в системе устанавливаются периодические движения, на­зываемые автоколебаниями,

Малое отклонение начальной точки, лежащей вокруг или на самом неустойчивом предельном цикле (рис. 5-7. б) приводит к уда­лению движения системы от периодического. Поэтому движение но неустойчивому предельному циклу физически нереализуемо. Устой­чивые и неустойчивые предельные циклы служат «водоразделами»,

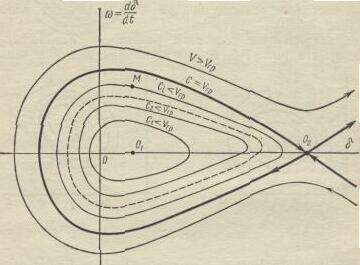
Рис. 3.8

отделяющими область с одним типом траекторий («разматывающиеся») от области с другим типом траекторий («сматывающиеся»». В неконсервативной системе имеется обычно конечное число предельных циклов.

При достаточно большом удалении от окрестности седла «усы» также служат «водоразделами» между движениями различного ха­рактера и называются сепаратрисами (кривая С =V_гр на рис. 3-8). Особые траектории— точки равновесия, сепаратрисы, предельные циклы разбивают всю фазовую плоскость на ряд областей, которые определяют полную качественную характеристику всех возможных видов движения системы. Для электрической системы с устройст­вами автоматического регулирования характерны все описанные виды особых траекторий. Сепаратриса разделяет затухающие пери­одические движения и расходящиеся апериодические движения. Она имеет важное техническое значение, так как область начальных условий, находящихся внутри сепаратрисы, определяет условия устойчивости после больших возмущений (динамической устойчивости электрической системы).

3-3. НАХОЖДЕНИЕ ДОСТАТОЧНЫХ УСЛОВИЙ УСТОЙЧИВОСТИ ПРИ БОЛЬШИХ ВОЗМУЩЕНИЯХ С ПОМОЩЬЮ ПРЯМОГО (ВТОРОГО) МЕТОДА ЛЯПУНОВА

Для определения устойчивости после больших возмущений (дина­мической устойчивости электрической системы) необходимо знать совокупность начальных отклонений параметров режима и их производных, при которых система вернется в положение равновесия (область устой­чивости). Эта совокупность ограничена в фазовом пространстве сепаратрисной поверхностью. Для отыскания поверхности, лежащей внутри области устойчивости и прибли­жающейся к сепаратрисной поверхности, можно применить прямой (второй) ме­тод Ляпунова, заключающийся в следующем. Обобщив известное положение физики (равновесное положение устойчи­во, если в нем потенциальная энергия имеет минимум), Ляпунов предложил на­ходить при выводе условий устойчивости вспомогательную функцию координат х_i изображающей точки в фазовом простран­стве V{x_i)- Эта функция должна быть одно­значна, дифференцируема, определенно по­ложительна вне положения равновесия и обращаться в нуль в по­ложении равновесия.

Если удается подобрать такую функцию V, что при любом дви­жении системы она уменьшается, т. е. dV/dt < 0, то система оказы­вается «устойчивой в большом».

Примером функции Ляпунова может служить функция

v = x₁² + x₂² +x₃².

В этом случае поверхность V =С в фазовом пространстве (рис. 5-9) есть сфера. Поверхности V=C, построенные для различных значе­ний С(С₁, C₂, С₃), не пересекаются, так как — V --

Рис. 3-9

однозначная функ­ция координат. Поэтому семейство представляет собой вложенные одна в другую замкнутые поверхности, причем поверхность с мень­шим С вложена в поверхность с большим С. Поверхность V=С при С—>0 стремится к точке равновесия О.

Пусть в какой-либо момент времени изображающая точка М₁ (рис. 5-9) находится на поверхности V › C₃; если при движении системы производная dV/di < 0, то с течением времени изображаю­щая точка перемещается к поверхности V =С₂ , где С₂< С₃. Следо­вательно, фазовая траектория пронизывает вторую поверхность, лежащую внутри первой. Если изображающая точка при движении пронизывает поверхности семейства в направлении снаружи внутрь и с течением времени неограниченно приближается к точке равно­весия, то выполняются достаточные условия устойчи­вости в большом. Однако условие dV/dt < 0 не является необ­ходимым признаком устойчивости, так как могут существовать

фазовые траектории, идущие от внутренних поверхностей к наруж­ным, но направляющиеся к особой траектории, например устойчи­вому предельному циклу.

Недостатки прямого метода Ляпунова—отсутствие общих приемов

отыскания функции Ляпунова и невозможность оценки, насколько достаточные условия устойчивости в большом (С_i < V_гр , рис, 5-8) уже, чем необходимые условия устойчивости, определяемые сепара­трисой С=V_гр· Одно из достоинств метода Ляпунова—сокращение времени численного счета переходных процессов после приложения большого возмущения для определения динамической устойчивости.

Численными методами рассчитывается переходный процесс от момента приложения до момента снятия возмущающей силы (на­пример, такая кратковременная аварийная ситуация, как короткое замыкание в электрической системе, длится 0,1—0,4с).

Если значения переменных послеаварийного режима, определен­ные в конце аварийной ситуации, находятся внутри фазовой пло­скости, ограниченной предварительно построенной функцией Ляпу­нова, то система устойчива в большом (или динамически устойчива).

Пример 3-1. Найти прямым методом Ляпунова условия устойчивости в боль­шом электрической системы, представленном схемой «станция - шины».

Запишем нелинейное дифференциальное уравнение движения синхронной ма­шины, соединенной с системой, в простейшей (консервативной) идеализации:

dδ/dt=ω; dω/dt=P_o/T_J—[EU/{xT_J )] sinδ. (3-20) Введем обозначения:

A=P_o /T_J ; b=eu/(x t_J).

Найдем функцию Ляпунова. Для электрической системы в консервативной идеализации при выборе функции Ляпунова используем энергетический подход, Функцию Ляпунова запишем в виде первого интеграла движения синхронной ма­шины—интеграла энергии. Разделив второе уравнение (5-20) на первое,получим

(dω/dt)(dδ/df) = (A—Bsinδ)/ ω (5-21)

Разделяя переменные и интегрируя уравнение (5-21), найдем

0,5ω² – Аδ – В cos δ = C. (5-22 )

Выражение (5-22) характеризует полную энергию системы (5-20). состоящую из кинетической Ο.5ω² и потенциальной Aδ + B cos δ. Траектории рассмотренной электрической системы на фазовой плоскости [δ, ω] являются контурами ( кри­вые C_i на рис. 5-8) постоянной полной энергии. Изменение полной энергии по времени запишем как

dC/dt = (дС/дω) (dω/dt) + (дС/дδ) (dδ/dt).

Используя (3-22) и (3-20), найдем

dC/dt=ω(A—B sinδ)—Aω)+Bωsinδ=0. (3-23)

Следующий из (3-23) вывод о равенстве нулю изменения полной энергии в контуре С физически означает, что система, переведенная в результате какого-либо возмущения из точки 0 в точку М, лежащую на траектории со значением Сi (рис. 3-8), будет совершать движение по этой траектории. Если эта траектория замкнутая, то движение будет устойчивым. Так как функция (3-22) знакоопределенная, то ее можно принять за функцию Ляпунова, поскольку она удовлетворяет требованиям, предъявляемым к функциям этого класса, а именно:

1) V (δ, ω) > О в некоторой области вокруг начала координат, совмещенного с устойчивым положением равновесия;

2) dV/dt > 0 во всем пространстве.

Областью устойчивости системы (3-20) является часть окружающего начало координат пространства,ограниченного самой большой замкнутой поверхностью C ==Vrp. соответствующей граничному значению функции Ляпунова. Эта гранич­ная—сепаратрисная—поверхность проходит через седловую точку (точка О₂ на рис. 5-8), которую необходимо определить.

Как известно, особые точки находятся приравниванием нулю правых частей исходных дифференциальных уравнений переходного процесса (5-20):

ω=0; A -- Bsinδ=0; δ_о=arcsin {А/В).

При А < В имеется два положения равновесия—центр Ο₁ [δ_о, 0] и седло О₂ [π—δ_о, О) (рис. 5-8).

Замкнутая часть сепаратрисной поверхности Vrp, проходящей через седло, определяет область устойчивости системы в большом Критерий устойчивости математически запишется как V = V_гр,

3-4. ИССЛЕДОВАНИЯ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ С ПОМОЩЬЮ ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ НЕЛИНЕЙНОСТЕЙ

Построение длительных колебательных процессов численными методами решения нелинейных дифференциальных уравнений может дать большую ошибку; кроме того, при этом невозможно получить какие-либо общие закономерности. Эти обстоятельства заставляют искать особые приемы для приближенного определения периодиче­ских решений нелинейных дифференциальных уравнений, характер­ных для синхронных машин в электрической системе. В этих при­емах используется разложение нелинейности в ряд Фурье при отыскании периодических решений и совокупного решения уравне­ний для каждой гармоники (метод гармонического баланса).

В случаях, когда амплитуды колебаний высших гармоник по от­ношению к первой малы и когда в ряду Фурье можно оставить только постоянные составляющие и первые гармоники, метод гар­монического баланса превращается в метод гармонической линеари­зации. Заметим, что условиями малости составляющих высших гармоник выполняются, если система обладает свойством фильтра. Объект исследования электрической системы—синхронная машина—обла­дает свойством фильтра тем сильнее, чем меньше ее демпфирование (амплитудно-частотная характеристика колебательной системы имеет резко выраженный резонанс, см, рис. 3-23). Цель метода гармони­ческой линеаризации состоит в том, чтобы вычислять параметры колебательного процесса—координаты средней точки колебаний (постоянные составляющие), максимальные отклонения от нее (ам­плитуды первой гармоники), время одного полного колебания, пе­риод или частоту. Однако предварительно нужно определить, будет ли процесс при данных параметрах системы, данном внешнем воз­действии и данных начальных условиях колебательным или моно­тонным. Иными словами, надо найти границы существования пери­одических решений. Для синхронной машины, работающей в элек­трической системе, синхронные колебания ограничиваются условиями

динамической устойчивости. При некоторых начальных условиях и внешних возмущениях, приводящих к нарушению динамической устойчивости, периодические решения (синхронные качания роторов синхронной машины) уже не существуют. Чтобы периодическое движение реально существовало, необходимо выполнение не только условия существования, но и условия устойчивости. Условия устой­чивости установившихся периодических движений в регулируемых электрических системах делят периодические границы областей ста­тической устойчивости на опасные и безопасные участки.

Пример 5-2. Определить максимально допустимую амплитуду колебаний не­линейной колебательной системы, превышение которой приводит к неустойчивости в большом. Применительно к синхронной машине, работающей параллельно с электрический системой, появление колебания ротора (либо свободного—вслед­ствие начального возмущения, либо вынужденного—вследствие внешней гармо­нической силы) с амплитудой выше критической oзначает нарушение синхронной динамической устойчивости, т, е. неустойчивости в большом. Определение макси­мально допустимых амплитуд колебаний, таким образом, является практически важной задачей для электрической системы.

Нелинейное дифференциальное уравнение, описывающее в некоторой идеали­зации электромеханические переходные процессы простейшей электрической системы, имеет вид:

d² δ/dt² + β dδ/dt + ω_o² sin δ = F(t).

Здесь

β = P_d[рад]/ T_J[c] ; ω_o² = E_qoU2πf/ T_J[c] x_d∑ [1/c²]

F (t}—внешняя сила; f—50 Гц—частота сети.

Если рассматривать большие колебания угла δ ротора синхронной машины относительно вектора напряжения системы и искать приближенное (гармоническая линеаризация) периодическое решение в виде ряда Фурье:

δ = a_o+ a₁ sin (ωt + φ₁ ),

где a_o—постоянная составляющая; a₁—амплитуда первой гармоники, то нелиней­ная функция в комплексной форме запишется как

sinδ = sin[a_o+a₁ sin (ωt + φ₁)] = ∑S_ne^jωnt = S_o +(S_—1 + S₁)e^jωt.

Здесь S_n—коэффициенты разложения в ряд Фурье:

S_o = J_o(a_o) sin a_o; S₁ = [2J₁ (a₁/a]ξ₁ cos a_o;

S_—1 [2J₁ (a₁)/a₁]ξ_—1cos a_o.

При этом J_o(a₁) и J₁(a₁) -- функции Бесселя первого рода; ξ₁ и ξ_--1—компексно - сопряженные

амплитуды колебания угла δ, связанные с действительной

амплитудой следующим соотношением:

ξ₁e^jωt + ξ_—1e^—jωt = a₁ sin(ωt + (a₁/2j )[e^{j(ωt + φ1)} e^{—j(ωt +φ1)}], откуда

ξ₁ = (a₁/2j) e^jφ1; ξ_—1 = --(a₁/2j) e^—jφ1.

Рассмотрим свободные колебания, когда в правой части (5-24) стоит момент турбины, определяющий установившееся значение угла δ = δ_o, т.е F(t) = ω_o² sin δ_0. Приравнивая коэффициенты при одинаковых гармониках, получим уравнении n = 0 и n =1) для постоянных составляющих и первых гармоник соответственно:

J_o( a₁) sin a_o = sinδo ; (3--25 )

(--ω² + jβω)ξ₁ + ω² [2J(a₁)/a₁]ξ₁ cos a_o = 0. (3—26)

(7-26)

Уравнение (3-25) определяет связь между средней точкой и амплитудой ко­лебания угла:

sin a_o = sinδ_o/[ J_o (a₁)] (3-27.)

Функция Бесселя J_o(a₁₎ уменьшается с увеличением a₁ (рис. 3-10), начинаясь при a—-0 от J_o (a₁ ). Уравнение (3-27) показывает, что при малых a₁ система

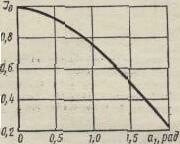
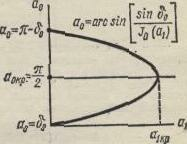
Рис. 3-10 Рис. 3.11