Статистика в электроэнергетике

Решение любых задач с применением теории вероятностей в тех случаях, когда используется их статистическое определение, невоз­можно без получения соответствующего статистического материала, базирующегося на большом количестве опытов или наблюдений. При этом возникают задачи, связанные с правильной обработкой статистических материалов и приданием им формы, удобной для последующего применения методов теории вероятностей. Раздел теории вероятностей, занимающийся регистрацией, обработкой и анализом статистических материалов, называется математической статистикой. .

Рассмотрим вопрос о точности определения статистической вероят­ности какого-либо события на основании опытов или наблюденийпо схеме независимых испытаний. Закон больших чисел (теорема Бернулли) утверждает) [Л.2]: при неограниченном возрастании числа испытаний вероятность того, что разность между наблюденной относительной частотой некоторого события А (равной m/n, где n—число испытаний, а m—число появлений события) и истинной вероятностью события p будет меньше любого самого ма­лого числа ε, стремится к единице, т. е. при достаточно большом числе испытаний вероятность ошибки в замене вероятности случайного события относительной частотой его появления стремится к нулю.

Однако бесконечно большое число испытаний недостижимо прак­тически приходится довольствоваться некоторым большим числом испытаний. При этом ошибка в определении вероятности по отно­сительной частоте события является также случайной величиной, имеющей ту или иную вероятность. Интегральная предельная тео­рема Муавра—Лапласа позволяет определить вероятность той или иной ошибки. Согласно этой теореме

где a и b --

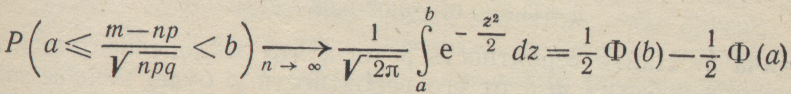
произвольные числа; р— истинная вероятность события; q = 1 – p.

Одно из следствий этой теоремы записывается следующим образом:

поэтому (при достаточно большом n)

(1-35)

где m/n— относительная частота появления события; ε—произволь­ное число; Φ(x) — интеграл вероятности [ Л.2 ] .

Это дает возможность определить приближенно вероятность ошибки ε в оценке вероятности события р. При определении ста­тистической вероятности какого-либо случайного события могут возникнуть три различных задачи, решение которых основывается на использовании формулы (1-35).

Пусть, например, событием будет аварийный выход в часы ве­чернего максимума энергосистемы какого-либо агрегата. Тогда числом испытаний будет число дней наблюдения п, а числом появлений события—число дней, когда данный агрегат находится в период максимума в аварийном состоянии т. При этом возможны три задачи.

Задача 1. Найти наименьшее число испытаний п, при котором разность относительной частоты m/n и вероятности события р не превышает заданной величины ε с заданной вероятностью β.

Согласно (1-35) _________

β=Φ[ε √n / (pq) ].

По таблицам интеграла вероятностей , используя зависимость β = Φ(α), при заданном значении β определяем α

_____

= ε√n /(pq) и далее находим минимальное число испытаний;

n=(α² / ε²)рq.

Пример 3-12. Пусть q = 0,02; p = 0,98; β = 0,99; ε = 0.01. Найдем наимень­шее число испытаний, при котором с вероятностью 0,98 разность относительной частоты и вероятности события не· превышает 0,01.

По таблицам интеграла вероятностей для Ф(а)==0,99 находим а=2,58. Тогда n = (2,58²./ 0,01²) * 0.02*0,98 = 1305.

Если требования к значению вероятности β понизить до β=0,95,то Φ (α) = =0,95; α = 1,96. При -атом n = (1,96 ² /0,01² ) * 0,98 * 0.02 = 753.

Наоборот, если требования к значению вероятности β повысить до 0,999, то Ф(а)==0,999; а=3,3. При этом

n = (3,3²/0,01²)*0,02*0,98=2134.

Задача 2. Найти вероятность β того, что отклонение относитель­ной частоты события т / п от его вероятности ρ будет меньше задан­ного числа ε при заданном числе испытаний п. Согласно (1-35) искомая величина

________

β = Ф[ ε√n / (pq) ],

поэтому сначала определяют α = ε√n /{pq), а затем по таблицам интеграла вероятности находят β = Φ(α).

Пример 3-13. Определить вероятиость того, что максимальное отклонение относительнон частоты события т/п от вероятности р==0,98 будет меньше

ε = 0,005 при числе испытании n = 1000, Исходя из условия, ______

α = ε √n / (pq) ] = 0,005 √1000/0,98·0,02 = 1,11.

По таблицам интеграла вероятности находим Ф(1,11) = 0,733. Следовательно, искомая вероятность равна 0.733. Если снизить требование к точносги. приняв ε = 0,01, то α = 2,22; β = Ф (2,22) = 0.973, т, с. верояность непревышения такой ошибки возрастет с 0 733 до 0.973. Если еще снизить требование к точности, то при ε = 0,02 значение α = 4,44 и β = Φ (4,44) = 0,999994.

Задача З. Найти макснмальное отклонение относительной частоты

события от его вероятности ρ при числе испытаний п, имеющее заданную вероятность β. По величине вероятности β = Φ (α) из та­блиц интеграла вероятности находим α, а затем

ε = √ pq/n.

Пример 3-14. Найти максимальное отклонение относительной частоты события от вероятности ρ =0,98, имеющее при числе испытаний n = 1000 вероятность β = 0.98.

Πυ значению Φ (α) =0,98 с помощью таблиц интеграла вероятности опреде­ляем α = 2,33, тогда

ε = 2,33)√0,02.0,98/1000 = 0,0105.