3.Транспортная задача линйного программирования

Симплекс-метод решения задачи линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые допускают решение более простыми методами. К ним, в частности, относится и транспортная задача.

Классическая транспортная задача ЛП формулируется следующим образом.

Имеется m пунктов отправления: А_1, А_{2, . . . . . .} : Аm_., в которых сосредоточены запасы какого-то однородного товара в количестве соответственно а₁, а₂, а_m , единиц. Имеется также n пунктов назначения:

В_1, В_{2, . . . . . . . .} В_m, подавших заявки соответственно на b₁, b₂, . . . . .b_n, единиц товара.

Предполагается , что сумма всех заявок равна сумме всех запасов.

(3.1)

Известна стоимость с _ij перевозки единицы товара от каждого пункта отправления Ai до каждого пункта назначения Bj . Таблица (матрица) стоимостей перевозки с _ij задана:

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех перевозок была минимальной.

Дадим этой задаче математическую формулировку. Обозначим x _{i j} - количество товара , направляемого из i-го пункта отправления Ai в j – й пункт назначения Bj ( i = 1, . . ., m; j = 1, . . . n). Неотрицательные переменные х₁₁, х₁₂,. . . ., х_mn ( число которых, очевидно, равно ( m × n ) должны удовлетворять следующим условиям:

1. Суммарное количество товара, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу товара в данном пункте. Это дает нам m условий-равенств;

х₁₁ + х₁₂ +. . . . + х_{1 n} = а₁ ,

х₂₁ + х₂₂ +. . . . + х_{2 n} = а₂ , (3,2)

. . . . . . . . . . . . . . . .. . . . . . . .

х m1 + х_m2 +. . . . + х_{m n} = а _m .

2. Суммарное количество товара , доставляемое в каждый пункт назначения изо во всех пунктов отправления , должно быть равно заявке, поданной каждым пунктом. Это даст n условий-равенств:

х₁₁ + х₂₁ +. . . . + х _m1 = b₁ ,

х₁₂ + х₂₂ +. . . . + х_m2 = b₂ , (3.3)

. . . . . . . . . . . . . . . .. . . . . . . .

х _1n + х_2n +. . . . + х_{m n} = b_n .

3. Суммарная стоимость всех перевозок, т.е. сумма величин х _{i j} , умноженных на соответствующие стоимости с _{i j} должна быть минимальной:

L = c₁₁ x₁₁ + c₁₂ x₁₂ + . . . . + c_1n x_1n + c₂₁ x₂₁ + c₂₂ x₂₂ + . . . .

c_2n x_2n + . . . . + c_m1 x _m1 + c_m2 x _m12 + . . . . + c_{m n} x _m n = min. (3.4)

Функция (3.4) линейна, ограниченная – равенства (3.2),(3.3) также линейны. Перед нами типичная задача с ограничениями – равенствами (ОЗЛП).

Как и всякую другую задачу линейного программирования, ее было бы решить симплекс-методом , но данная задача имеет некоторые особенности, позволяющие решить ее более просто. Причиной является то, что все коэффициенты при переменных в уравнениях (3.2),(3.3) равны единице. Кроме того имеет значение структура связи между условиями. Нетрудно убедиться, что не все m + n уравнений нашей задачи являются независимыми. Действительно, складывая между собой все уравнения (3.2) и все уравнения (3.3) мы должны получить одно и то же, в силу условия (3.1). Таким образом, условия (3.2) , (3.3) связаны одной линейной зависимостью , и фактически из этих уравнений только m + n -- 1, а не m + n являются линейно независимыми. Значит, ранг системы уравнений (3.2),(3.3) равен

r = m + n --1

а , следовательно, можно разрешить эти уравнения

относительно m + n --1 базисных переменных, выразив их через остальные, свободные.

Подсчитаем количество свободных переменных. Оно равно:

k = mn -- (m + n –1 ) = mn -- m – (n –1) =

= m(n -- 1) – (n –1) = (m—1) (n –1).

Мы знаем, что в задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР , где по крайней мере k переменных обращается в нуль. Значит в нашем случае для оптимального плана перевозок по крайней мере (m—1) (n –1) значений x _{i j} должны быть равны нулю.

Терминология. Независимо от того , что, транспортируется, откуда и куда ( в условиях электроснабжения это может быть передача электроэнергии от электростанций потребителям)

значения x _{i j} количества единиц транспортируемого продукта, направляемых из пункта А_i

в пункт В_j мы будем называть п е р е в о з к а м и.

Любую совокупность значений (x _{i j} ) (i = 1,. . . . , m ; j = 1, . . . n) , будем называть планом перевозок, или просто планом.

План (x _{i j} ) будет называться д о п у с т и м ы м , если он удовлетворяет условиям (3.2).(3.3)

(балансовым условиям)6 все заявки удовлетворены, все запасы исчерпаны.

Допустимый план будет о п о р н ы м , если в нем отличны от нуля не более r = m + n --1

базисных перевозок x _{i j ,} а остальные равны нулю.

План (x _{i j} ) будем называть оптимальным, если он среди всех допустимых планов приводит к наименьшей стоимости всех перевозок.

Методы решения транспортной задачи сводятся к простым операциям непосредственно с таблицей, где в определенном порядке записаны все условия транспортной задачи. Такую таблицу называют т р а н с п о р т н о й т а б л и ц е й.

В транспортной таблице записываются

1) пункты отправления и назначения,

2) запасы, имеющиеся в пунктах отправления,

3) заявки, поданные пунктами назначения,

4) стоимости перевозок из каждого пункта отправления в каждый пункт назначения.

Стоимости перевозок помещают в правом верхнем углу каждой ячейки, с тем чтобы в самой ячейке при составлении плана помещать перевозки x _{i j} .

Образец заполнения транспортной таблицы

Таблица 3.1

пн по\	B1	B2		Bn	Запасы ai
А1	С11	С12		С1n	a1
А2	с21	с22		с2n	a2
………………	………………	………………………….	…………………………	…………………….
Аm	сm1	сm2		сmn	a m
Заявки	b1	b2		bn	∑ai = ∑bJ

Поскольку ранг системы уравнений-ограничений ТЗ равен r = n + m – 1, где

m – число строк , а n – число столбцов, следует утверждать, что в каждом опорном плане, включая и оптимальный, будут отличны от пуля не более чем r = n + m – 1 перевозок.

Ячейки (клетки) таблицы, в которых записываются отличные от нуля перевозки,

Называют базисными, а остальные (пустые) свободными.

З.1. Нахождение опорного плана

Наибольшее распространение для нахождения начальных опорных планов получили:

-- метод северо- западного угла и

-- метод минимального элемента .

Метод северо-западного угла используют для нахождения произвольного опорного плана ТЗ. Основную идею метода рассмотрим на конкретном примере.

Пример 1. Условия ТЗ заданы транспортной таблицей (табл. 3.1).

Таблица 3.1

Требуется найти опорное решение (построить опорный план).

Решение. Будем заполнять таблицу 3.1 перевозками постепенно , начиная с левой верхней ячейки(1.1) ( северо-западного угла).Будем рассуждать при этом следующим образом.

Пункт В₁ подал заявку на 18 единиц товара . Удовлетворим эту заявку за счет запаса 48, имеющегося в пункте А₁, и запишем перевозку 18 в клетке (1.1). После этого заявка пункта В₁ удовлетворена, а в пункте А₁ осталось еще 30 единиц товара. Удовлетворим за счет них заявку пункта В₂ (27 единиц), запишем 27 единиц в клетке (1,2); оставшиеся 3 единицы пункта А₁ назначим пункту В₃ . В составе заявке пункта В₃ остались неудовлетворенными 39 единиц. Из них 30 покроем за счет пункта А₂ , чем его запас будет исчерпан, и еще 9 возьмем из пункта А₃. Из оставшихся 18 единиц пункта А₃ 12 выделим пункту В₄ ; оставшиеся 6 единиц назначим пункту В₅, что вместе со всеми 20 единицами пункта А₄ покроет его заявку (табл. 3.2).

Таблица 3.2

На этом распределение запасов закончено. Каждый пункт назначения получил согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке равна запасу, а в столбце – заявку.

Таким образом, нами составлен план перевозок , удовлетворяющий балансовым условиям. Полученное решение является не только допустимым , но и опорным решением ТЗ.

Клетки таблицы , в которых стоят ненулевые перевозки , являются базисными, их число удовлетворяет условию r = n + m – 1 = 8. Остальные клетки -- свободные , в них стоят нулевые перевозки , их число равно (n – 1)(m – 1) = 12.Значит, составленный план -- опорный и поставленная задача построения опорного плана решена.

Но является ли этот план оптимальным? Нет, так как при его совершенно не учитывались стоимости перевозок с_{i j} . И даже, если мы стоимость этого плана перевозок

18 10 + 27 8 + 3 5 + 30 8 + 9 10 + 12 8 + 6 7 + 20 8 = 1039

гарантировать, что этот план оптимальный еще нельзя. Ниже мы рассмотрим способы улучшения

плана с целью получения оптимального.

Пример 2. Особенности построения «вырожденного плана»

План , в котором некоторые из базисных перевозок оказываются равными нулю , называют «вырожденным»

Дана транспортная таблица (табл.3.3) Построить опорный план.

Решение. Применяя метод северо-западного угла, получим таблицу 3.3.

Опорный план составлен. Особенностью его является то, что в нем только шесть, а не восемь отличных от нуля перевозок. Значит, некоторые из базисных перевозок , которых должно быть

быть m + n -- 1 = 8, оказались равными нулю.

Отчего это произошло ? При распределении запасов по пунктам назначения

в некоторых случаях остатки оказывались равными нулю и в соответствующую клетку не попадали.

Такие случаи «вырождения « могут возникать не только при составлении опорного плана, но и при его преобразовании, оптимизации.

В дальнейшем нам удобно будет всегда в транспортной таблице m + n -- 1 базисных клеток , хотя в некоторых из них, может быть, будут стоять и нулевые значения перевозок. Для этого можно ничтожно мало изменить запасы или

Таблица 3,3

Таблица 3.4

Таблица 3.5

заявки , так чтобы общий баланс не нарушился , а лишние «промежуточные» балансы уничтожались. Достаточно в нужных местах изменить запасы или заявки , например, на величину ε , а после нахождения оптимального решения положить ε = 0.

Как перейти от вырожденного плана к невырожденному можно понять на примере таблиц 3.4 и 3.5. Изменим слегка запасы в первой строке и положим их равными 20 + ε . Кроме того, в третьей строке проставим запасы 25 + ε. Чтобы «свести баланс» , в четвертой строке ставим запасы 20 -- 2 ε (табл. 3,5). Для этой таблицы строим опорный план методом северо-западного угла.

В табл. 3,5 уже содержится столько базисных переменных, сколько требуется:

m + n -- 1 = 8. В дальнейшем после оптимизации плана , можно будет положить

ε = 0.

Метод минимального элемента позволяет построить начальный опорный план

транспортной задачи и является вариантом метода северо-западного угла , учитывающего специфику матрицы С = c _{i j .} В отличие от метода северо-западного угла данный метод позволяет сразу получит достаточно экономичный план, сокращая количество итераций.

Смысл метода заключается в том , что элементы матрицы С нумеруют , начиная от минимального в порядке их возрастания , затем в этом же порядке заполняют матрицу Х. Другими словами сначала удовлетворяют заявки , используя самые дешевые перевозки, а затем по мере возрастания их стоимости.

3.2. У л у ш е н и е п л а н а п е р е в о з о к.

Ц и к л п е р е с ч е т а

План перевозок можно улучшить, перенося некоторые перевозки без нарушения баланса из клетки в клетку по замкнутому циклу. Ц и к л о м в транспортной таблице называют несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90 ˚. Ценой цикла называют увеличение перевозок при перемещении одной единицы груза по означенному циклу. Обозначим цену цикла через γ, При перемещении k единиц товара по циклу Ц стоимость перевозок увеличивается на k γ,

Очевидно для перемещения плана имеет смысл перевозки только по тем циклам, цена которых отрицательна. Каждый раз , когда нам удастся совершить такое перемещение, стоимость , стоимость плана уменьшается на соответствующую величину k γ.

Так как перевозки не могут быть отрицательными, Мы будем пользоваться только теми циклами, отрицательные вершины которых лежат в базисных клетках таблицы, где стоят положительные перевозки. ( условимся отмечать знаком «+» те вершины цикла, в которых перевозки увеличиваются, знаком «-« -- » - те вершины, в которых они уменьшаются.

Метод последовательного улучшения плана перевозок и состоит в том, что в таблице отыскиваются циклы с отрицательной ценой, по ним перемещаются перевозки, и план улучшается до тех пор , пока циклов с отрицательной ценой уже не останется. Приэтом при каждом шаге (цикле) заменяют одну свободную переменную на базисную, т.е. заполняют одну свободную клетку и взамен ее освобождают одну из базисных клеток. Общее количество базисных клеток остается неизменным и равным

m + n -- 1 .

Пример 3. Найти оптимальный план для транспортной задачи, приведенной в таблице 3.6.

Таблица 3.6

Решение. Составляем опорный план методом северо-западного угла .(табл.3.7)

Стоимость этого плана равна: 22 • 10 + 9 • 7 + 25 • 6 + 23 • 5 + 18 • 6 + 20 • 7 = =796.

Число базисных переменных, как и полагается в невырожденном случае, равно

r = m + n – 1 = 3 + 4 -- 1 = 6.

Попробуем улучшить план, заняв свободную клетку (2,4) с минимальной стоимостью 4. Цикл, соответствующий этой клетке, показан в табл. 3.7. Цена этого цикла равна γ = 4 –7 + 6 = -- 2.

Таблица 3.7

По этому циклу мы можем переместить максимум 20 единиц товара (чтобы не получить в клетке (3,4) отрицательной перевозки).Новый улучшенный план показан в табл. 3.8.

Таблица 3.8

Cтоимость этого плана L₂ = 796 + 20 ( -- 2) = 756. В нем по-прежнему шесть базисных клеток.

Для дальнейшего улучшения плана обратим внимание на свободную клетку (2,1) со стоимостью . Цикл, соответствующий этой клетке, показан в табл. 3.8; цена его 7 – 6 + 5 –10 = --4. По этому циклу переместим 22 единицы товара , чем уменьшим стоимость перевозок до L₃ = 756 + 22 (--4) = 668 (см. табл. 3.9).

Таблица 3.9

Продолжаем дальше улучшить этот план , подсчитывая цены циклов, начинающихся положительной вершиной в свободной клетке. Просматриваем имеющиеся свободные клетки таблицы 3.9 и определяем цену цикла каждой из них. Все эти цены (можно проверить) или положительные или нулевые , следовательно, никакое дальнейшее циклическое перенесение перевозок не может улучшить план перевозок.

Таким образом, план, полученный в табл. 3.9 является оптимальным.

3.3. Р е ш е н и е т р а н с п о р т н о й з а д а ч и

м е т о д о м п о т е н ц а л о в

Распределительный метод решения ТЗ обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. Предлагаемый далее м е т о д п о т е н ц а л о в позволяет автоматически выделять циклы с отрицательной ценой и определять их цены.

Идея метода потенциалов сводится к следующему. Представим себе, что каждый из пунктов отправления А _i вносит за перевозку единицы товара какую-то сумму α _i ; в свою очередь , каждый из пунктов назначения В_j также вносит за перевозку товара (все равно куда) сумму β _j ; Эти платежи передают ся некоторому третьему лицу «перевозчику».

Обозначим

α _i + β _j = с_{ί j} * ( i = 1, . . ., m; j = 1, . . . , n)

и будем называть величину с_{ί j} * «псевдостоимостью» перевозки единицы товара из

А _i в В_{j .} Платежи не обязательно должны быть положительными.

Примем без доказательств следующие положения.

1. Суммарная псевдостоимость любого допустимого плана перевозок при заданных платежах (α _i , β _j ) одна и та жа и от плана к плану не меняется.

2. Если для всех базисных клеток плана (х_{i j} > 0)

α _i + β _j = с_{ί j} * = с_{ί j ,}

а для всех свободных клеток (х_{i j} = 0)

α _i + β _j = с_{ί j} * ≤ с_{ί j ,}

то план является оптимальным и никакими способами улучшен быть не может.

Можно показать, что эта теорема справедлива и для вырожденного плана, в котором некоторые из базисных переменных равны нулю.

Итак, признаком оптимальности плана (х_{i j} ) является выполнение двух условий:

с_{ί j} * = с_{ί j} для всех базисных клеток; (3.5)

с_{ί j} * ≤ с_{ί j} для всех свободных клеток. (3.6)

План, обладающий таким свойством, называется п о т е н ц и а л ь н ы м, а соответствующие ему платежи (α _i , β _j ) -- п о т е н ц а л а м и пунктов А _i , В_j

( i = 1, . . ., m; j = 1, . . . , n).

Свойство платежей. При улучшении плана нам помогает следующее свойство платежей и псевдостоимостей:

Какова бы ни была система (α _i , β _j ) , удовлетворяющая условию (3.5), для каждой свободной клетки цена цикла пересчета равна разности между стоимостью

с_{ί j} и псевдостоимостью с_{ί j} * в данной клетке:

γ _{i j} = с_{ί j} -- с_{ί j} * .

Пример. Решить методом потенциалов ТЗ, заданную в таблице 3.1, где имеется первый опорный план, составленный по способу северо-западного угла.

Таблица 3.10

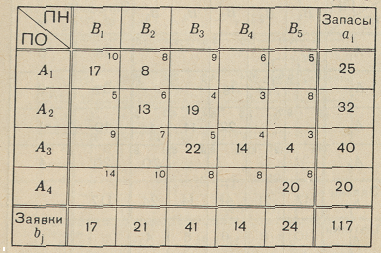
Решение. Приписываем к таблице 3.10 снизу добавочную строку для платежей β _j , справа – добавочный столбец для платежей α _i (табл. 3.11).

Таблица 3.11

Псевдостоимости с_{ί j} * = α _i + β _j записываем в левом верхнем углу каждой клетки, а стоимости – в правом верхнем углу.

Один из платежей , например, α ₁ , выбираем произвольно, полагая, скажем ,

α ₁ = 0. Для каждой базисной клетки псевдостоимость с_{ί j} * = α _i + β _j должна быть равна стоимости с_{ί j} .

Итак, положим α ₁ = 0 , находим из условия

α ₁ + β ₁ = 10; 0 + β ₁ = 10; β ₁ = 10,

а из условия

α ₁ + β ₂ = 0 + 8 ; β ₂ = 8.

Продолжая эту процедуру, находим:

α ₂ + β ₂ = α ₂ + 8 = 6; α ₂ = -- 2;

-- 2 + β ₃ = 4; β ₂ = 6;

α ₃ + 6 = 5; α ₃ = -- 1;

-- 1 + β ₄ = 4; β ₄ = 5;

--1 + β ₅ = 3, β ₅ = 4;

α ₄ + 4 = 8, α ₄ = 4.

Так как не все псевдостоимости в свободных клетках табл.3.11 удовлетворяют условию с_{ί j} * ≤ с_{ί j} , план, приведенный в табл, 3.11, не является оптимальным. Попробуем улучшить его , переводя в базисные одну из свободных клеток, для которых

с_{ί j} * > с_{ί j ,} например, клетку (2,1). Строим соответствующий этой клетке цикл (показан в табл. 3.11) . Цена этого цикла 5 -- 8 = -- 3.Перенесем по этому циклу 13 единиц товара (больше нельзя, чтобы перевозки в клетке (2,2) не стали отрица -- тельными), уменьшим стоимость плана на 13 • 3 = 39 и перейдем к таблице 3.12.

Таблица 3.12

Вычисляем для плана табл. 3.12 новые значения платежей, по-прежнему полагая

α ₁ = 0. Видим, что в табл. 3.12 все еще есть свободные клетки, для которых с_{ί j} * > с_{ί j ,}

например, (1,4). Цикл этой клетки показан в табл. 3.12. Перенос четырех единиц по этому циклу приводит к плану, представленному ( со своими платежами и псевдостоимостями) в таблице 3.13. Этот план все еще не оптимальный. Перенося по циклу, соответствующему свободной клетке (4,3) , 20 единиц товара, получаем новый план (табл. 3.14) с новыми платежами и псевдостоимостями.

В табл. 3.14 уже все псевдостоимости не превосходят соответствующих стоимостей, значит, этот план о п т и м а л ь н ы й . Потенциалы пунктов найдениы и равны соответственно:

α ₁ = 0; α ₂ = --3; α ₃ = -- 2; α ₄ = 1;

β ₁ = 8; β ₂ = 8 ; β ₃ = 7; β ₄ = 6; β ₅ = 5.

Таблица 3.13

При анализе этих значений нельзя забывать, что одно из них (в нашем случае α ₁ ) назначено произвольно (α ₁= 0), поэтому потенциалы (или равносильные платежи) пунктов достаточно условны. Важно, что их сумма для всех перевозок, отличных от нуля, равна сумме стоимостей , проставленных в соответствующих клетках. Если смотреть на эти платежи не с точки зрения каждого пункта в отдельности, а с точки зрения всей совокупности пунктов (А,В) , то безразлично, какой из пунктов платит больше, а какой – меньше.

Таблица 3.14

В случае, если план будет вырожденным, сценарий применения метода потенциалов будет аналогичным. Разница в том, что для получения первоначального опорного плана вводят ε – изменения запасов.

Мы рассмотрели только такую транспортную задачу, в которой сумма запасов равна сумме заявок. Однако существуют и другие типы ТЗ, например, ТЗ с неправильным балансом т др. Подходы к решению подобных задач широко описаны литературе, например, [Л 1,2 ].

Темы расчетно-графических работ

по математическим задачам электроэнергетике

РГР № 1

Составить реферат по разделу «Применение методов теории вероятности в задачах электроэнергетики (12 – 15 с ). В реферате обязательно отразить следующие вопросы:

1) понятие случайного события, случайной величины, случайного процесса. Примеры из области электроэнергетики.

2) определение математического ожидания, дисперсии, стандартного отклонения.

3) понятие о корреляции. Определение коэффициента корреляции.

4)понятие о математической статистике.

РГР № 2 Задача (Пример расчета смотри : Пример 1-18 стр 35)

В энергосистеме в течение шести суток наблюдались следующие мощности в 1000 МВт за характерные часы суток.

( 4 12 16 19 24 )

Часы суток	Мощность спроса за сутки в 1000 МВт
	первые	вторые	третьи	четвертые	пятые	шестые
4	а1	б1	в1	д1	е1	ж1
10	а2	б2	в2	д2	е2	ж2
16	а3	б3	в3	д3	е3	ж3
19	а4	б4	в4	д4	е4	ж4
24	а5	б5	в5	д5	е5	ж5

Рассматривая спрос как случайный процесс, 1. определить математические ожидания, дисперсии, стандартные отклонения и корреляционные коэффициенты для указанных сечений; 2. предсказать на основе этих данных спрос в 19 часов, если в 10 часов утра наблюдался спрос а2 МВт. Данные для расчета
№вар	1	2	3	4	5	6	7	8	9	10
а1	5	5	5	6	4	5	4	5	5	6
а2	12	11	13	11	11	12	11	11	12	12
а3	10	8	9	8	7	9	9	8	9	8
а4	19	17	20	17	16	17	18	19	20	21
а5	9	9	12	9	10	10	10	9	11	10
б1	6	4	5	4	7	6	5	4	6	7
б2	10	10	12	10	11	12	10	9	8	11
б3	8	8	9	8	9	10	9	8	9	10
б4	17	17	18	18	17	19	20	18	17	18
б5	9	8	10	9	9	8	9	8	7	9
в1	4	6	7	6	6	5	4	5	4	5
в2	10	11	11	12	13	12	13	11	12	12
в3	8	8	9	9	8	7	8	7	8	8
в4	17	18	19	18	17	18	19	20	21	20
в5	9	10	9	8	8	9	8	10	10	10
д1	7	4	6	5	7	6	5	7	6	6
д2	14	10	11	12	13	14	14	14	13	12
д3	11	8	8	10	9	8	9	8	9	8
д4	20	17	17	19	19	19	17	18	20	17
д5	11	9	9	9	10	9	10	9	11	9
е1	5	6	6	6	5	5	6	6	6	6
е2	12	11	13	11	12	11	12	11	12	13
е3	9	8	9	8	9	8	9	7	8	9
е4	18	19	20	18	19	20	17	18	19	20
е5	9	8	10	9	8	10	9	8	9	10
ж1	4	5	6	4	6	6	4	5	6	7
ж2	12	11	12	11	12	11	13	12	12	12
ж3	7	8	7	8	7	8	7	8	7	8
ж4	18	19	18	20	21	22	21	20	21	22
ж5	8	9	8	8	9	9	8	10	10	9

. Данные для расчета (продолжение)
№вар	11	12	13	14	15	16	17	18	19	20
а1	5	6	5	6	5	5	5	6	6	6
а2	12	11	13	11	12	11	12	11	12	13
а3	9	8	9	8	9	8	9	7	8	9
а4	18	19	20	18	19	20	17	18	19	20
а5	9	8	10	9	8	10	9	8	9	10
б1	4	5	6	4	6	6	4	5	6	7
б2	12	11	12	11	11	11	13	12	12	12
б3	7	8	7	8	8	7	7	8	7	8
б4	18	19	18	20	22	21	21	20	21	22
б5	8	9	18	8	9	8	8	10	10	9
в1	5	4	5	4	4	5	6	5	5	4
в2	11	10	12	12	12	10	12	11	13	10
в3	8	7	8	7	8	7	8	7	8	9
в4	19	20	20	20	20	18	19	18	17	18
в5	9	10	9	9	7	8	9	9	8	9
д1	4	5	6	5	4	6	5	6	6	5
д2	14	12	14	12	12	13	12	13	12	15
д3	9	8	7	8	9	8	7	8	7	9
д4	20	21	22	19	19	19	20	19	20	20
д5	9	7	7	9	8	9	8	7	11	9
е1	5	6	6	6	5	5	6	6	6	6
е2	12	11	13	11	12	11	12	11	12	13
е3	9	8	9	8	9	8	9	7	8	9
е4	18	19	20	18	19	20	17	18	19	20
е5	9	8	10	9	8	10	9	8	9	10
ж1	4	5	6	4	6	6	4	5	6	7
ж2	12	11	12	11	12	11	13	12	12	12
ж3	7	8	7	8	7	8	7	8	7	8
ж4	18	19	18	20	21	22	21	20	21	22
ж5	8	9	8	8	9	9	8	10	10	9

Пример расчета смотри : Пример 1-18 стр 35

РГР № 3 ( См. стр 47-57)

Имеется m электростанций: А₁, А₂,. . . . А _m, которые могут вырабатывать электроэнергию в количестве соответственно а₁, а_{2 ., . . . .} а _m МВТ.ч . Имеется n потребителей электроэнергии В₁, В₂,. . . ., В n, подавших заявки соответственно на в_1, в_2, . . . . , в _n МВТ.ч . Предполагается, что сумма всех заявок равна равна суммарной мощности всех электростанций.

Известна стоимость с _{i j} передачи электроэнергии от каждой электростанции A_i

до каждого потребителя В _j .Условия задачи заданы транспортной таблицей.

Требуется составить такой план передачи энергии от электростанций потребителям, чтобы все заявки были выполнены и при этом суммарная стоимость передачи энергии

была минимальна.

Вариант 1 Вариант 2

					a i
	1	8	2	3	30
	4	7	5	1	50
	5	3	4	4	20
bj	15	15	40	30

					a i
	2	4	5	1	60
	2	3	9	4	70
	3	4	22	5	20
bj	40	30	35	45

Вариант 3 Вариант 4

					a i
	2	9	3	4	30
	4	7	5	1	50
	5	3	4	4	20
bj	15	15	40	30

					a i
	2	4	5	1	60
	3	4	10	5	70
	3	4	22	5	20
bj	50	30	40	30

Вариант 5 Вариант 6

					a i
	2	4	5	1	60
	2	3	9	4	70
	3	4	2	4	20
bj	40	30	30	50

					a i
	3	4	5	1	60
	2	4	8	4	70
	3	4	12	6	20
bj	40	30	30	50

Вариант 7 Вариант 8

					a i
	2	9	3	5	30
	4	7	6	1	50
	5	4	3	4	20
bj	15	15	40	30

					a i
	2	3	4	1	60
	3	4	10	5	70
	3	4	2	5	20
bj	40	35	45	30

Вариант 9 Вариант 10

					a i
	10	5	7	4	40
	7	4	9	10	25
	6	14	8	7	35
bj	15	15	40	30

					a i
	2	4	3	2	60
	3	1	2	3	65
	5	4	1	5	70
bj	40	60	70	25

Вариант 11 Вариант 12

					a i
	3	9	3	4	40
	4	2	5	1	25
	5	3	8	4	35
bj	15	15	40	30

					a i
	1	4	5	1	60
	3	2	10	5	70
	3	4	3	5	20
bj	40	30	50	30

Вариант 13 Вариант 14

					a i
	2	4	5	2	60
	2	3	8	4	70
	3	6	2	4	45
bj	40	50	30	55

					a i
	3	5	6	1	60
	2	7	8	4	50
	3	9	10	6	70
bj	40	45	35	60

Вариант 15 Вариант 16

					a i
	3	10	4	6	20
	5	8	7	1	50
	4	5	3	4	70
bj	55	15	40	30

					a i
	4	3	4	3	60
	3	1	10	5	50
	8	5	2	9	20
bj	40	30	30	30

Вариант 17 Вариант 18

					a i
	5	4	5	2	60
	2	6	1	4	70
	3	6	2	4	40
bj	40	50	30	50

					a i
	3	5	6	1	60
	2	6	9	4	50
	3	7	10	6	40
bj	40	15	50	45

Вариант 19 Вариант 20

					a i
	3	11	4	6	20
	5	8	7	1	50
	4	5	3	9	60
bj	15	45	40	30

					a i
	4	3	4	9	60
	3	2	10	5	50
	1	5	2	9	20
bj	40	45	15	30