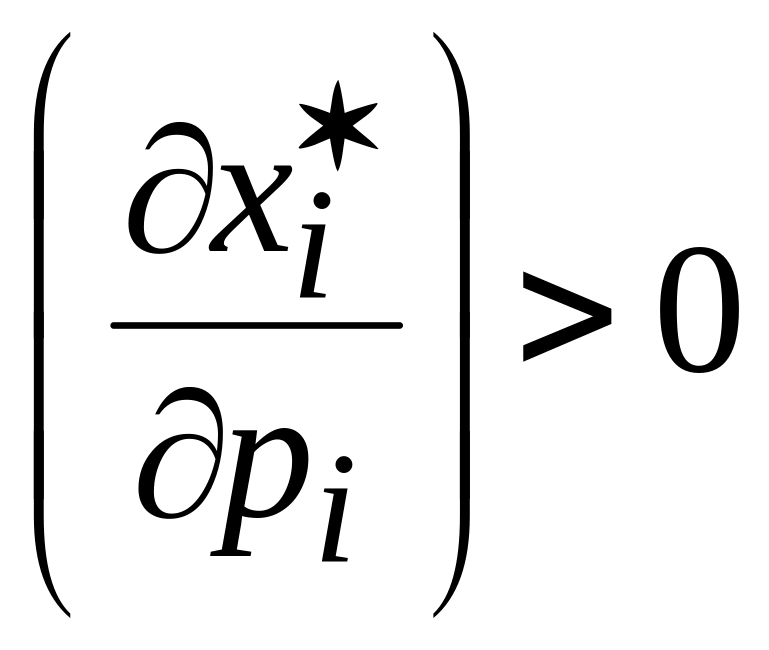2.3.Задача оптимального потребления

Введем бюджетное ограничение, которое означает, что денежные расходы на товары и услуги не могут превышать дохода. Обозначим

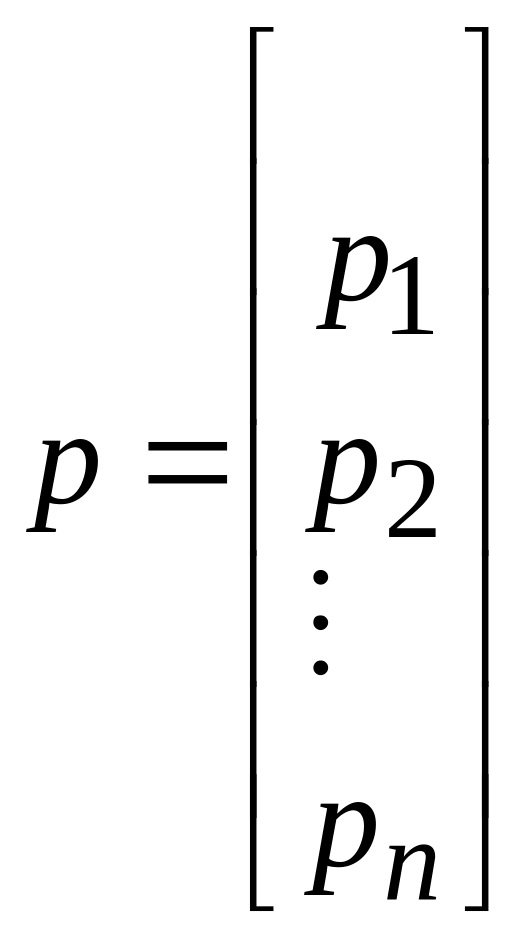вектор цен товаров. Его компонента р_і - цена единицы i-го товара .

Обозначим I - денежный доход. Тогда бюджетное ограничение:

(2.16)

Оптимальная задача потребления состоит в следующем: необходимо найти вектор , который является решением задачи

, (2.17)

где - строго вогнутая функция.

Ранее было принято допущение о том, что матрица вторых производных отрицательно определена. Левая часть ограничения в задаче (2.17) – линейная функция. Поэтому она – выпуклая функция х. Таким образом ограничение в (2.17) выпуклую допустимую область. Следовательно, (2.17) – представляет задачу максимизации строго вогнутой функции на выпуклом множестве. Такая задача имеет единственное решение. Поэтому согласно теоремы Куна-Таккера необходимые и достаточные условия максимума:

, (2.18)

где - градиент , - множитель Лагранжа, - нулевой n-мерный вектор.

Решим (2.17), используя (2.18). Пусть =0, тогда из (2.18) , что противоречит предположению (2.12). Тогда > 0. Следовательно, из (2.18) .

Таким образом, решение х^* удовлетворяет условию: , оно определяет точку в С. Эта точка называется точкой спроса.

Пример. Пусть n=2, тогда из (2.18) получаем:

- соответствует первому ограничению (2.18),

- второе ограничение в (2.18).

Координаты точки спроса является решением данной системы уравнений. Геометрически решение находится в точке касания бюджетной прямой и кривой безразличия (линии равного уровня), см. рис.2.4.

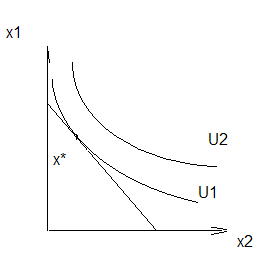
Рис.2.4.

На нем точка касания прямой и кривой безразличия U1 – решение. . - называется точкой спроса.

Оптимальный множитель Лагранжа

> 0 (2.19)

называется предельной полезностью добавочного дохода. Иногда называют иногда предельной полезностью денег. Согласно (2.19) -количество, на которое увеличится оптимальный уровень полезности, если доход увеличится на малую величину.

Решение (2.17), может быть представлено в виде функций коэффициентов левой части и правой части ограничения, т.е.

,

где f(p,I) – вектор-функция: f(p,I)=

Первое векторное выражение можно записать:

. (2.20)

Это уравнение называется функцией спроса на -й товар.

Важное свойство функций спроса – их однородность нулевой степени. Это означает, что

f(λp,λI)=λ⁰f(p,I)=λf(p,I), (2.21)

где .

Это свойство вытекает из постановки задачи. Если обе части ограничения умножить на λ, то результат не изменится, т.к. не изменится ограничение.

В силу свойства (2.21) спрос зависит от отношения цен.

Положим в (2.21) λ= , тогда

.

Можно выбрать .и

Краткое резюме: - вогнутая функция, имеет линии равного уровня. Точка спроса – единственная. Точка спроса находится на касательной к кривой равного уровня, которая в тоже время является кривой безразличия: функция полезности для всех точек на этой кривой одинакова.

2.4.Сравнительная статика потребления

В предыдущем разделе было установлено, что точки спроса удовлетворяет уравнению . Оно вытекает из второго уравнения в (2.18). Но должно удовлетворять и первому условию из двух необходимых и достаточных условий максимума (2.18). Таким образом,

(2.22)

Представляет интерес определение чувствительности и предельной полезности к изменению цен и дохода. Эту чувствительность будем измерять с помощью частных производных этих величин. Введем матрицу

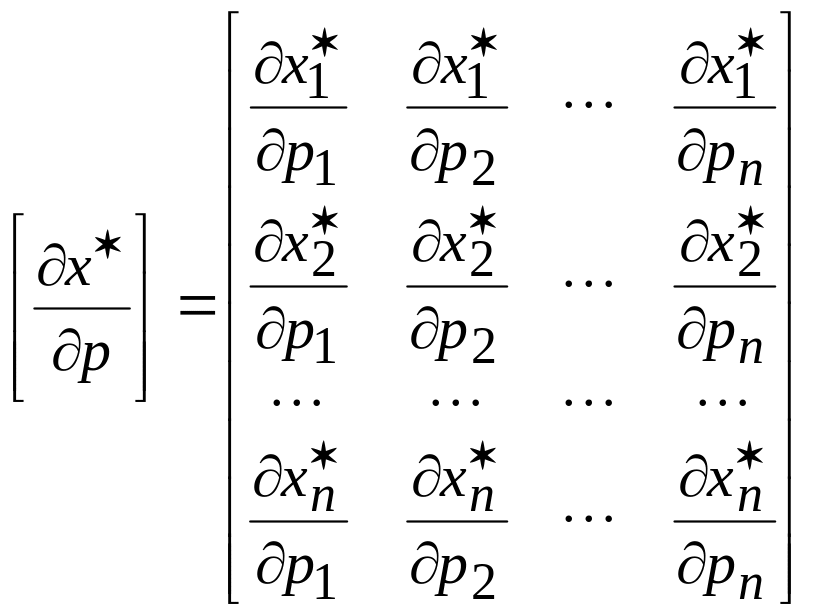(2.23)

Размерность

Чувствительность определяется градиентом

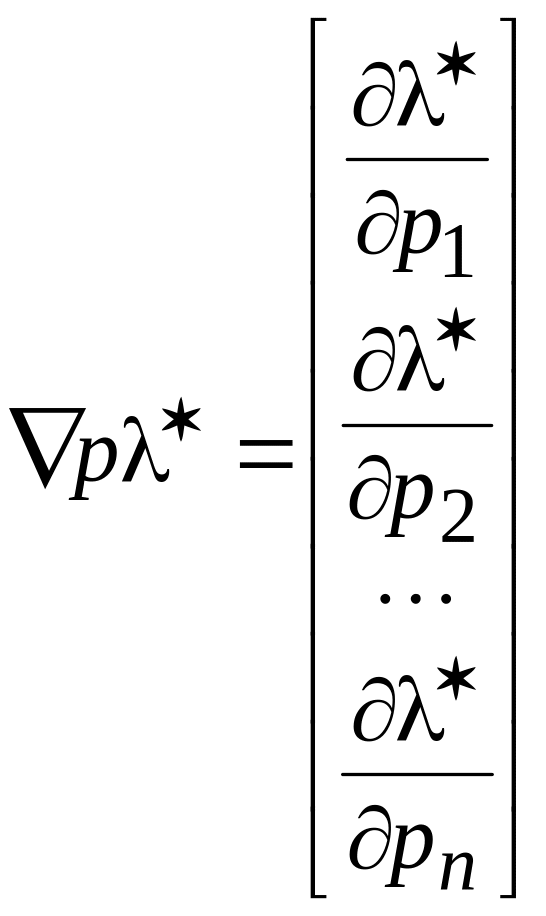. (2.24)

При определении и важно определить компенсированное изменение цены, т.е. такое ее изменение, которое компенсируется таким образом, чтобы функция полезности не изменилась. Это означает, что потребитель ничего не потеряет от изменения цены, т.е. его функция полезности не изменится. При этом величины, характеризующие чувствительность отношений спроса к вектору цены , а именно матрицы и градиента должны равняться некоторым величинам:

, ,

где матрица и вектор неизвестны и их необходимо найти.

Определим теперь чувствительность точки спроса и предельной полезности к изменению дохода I с помощью выражений:

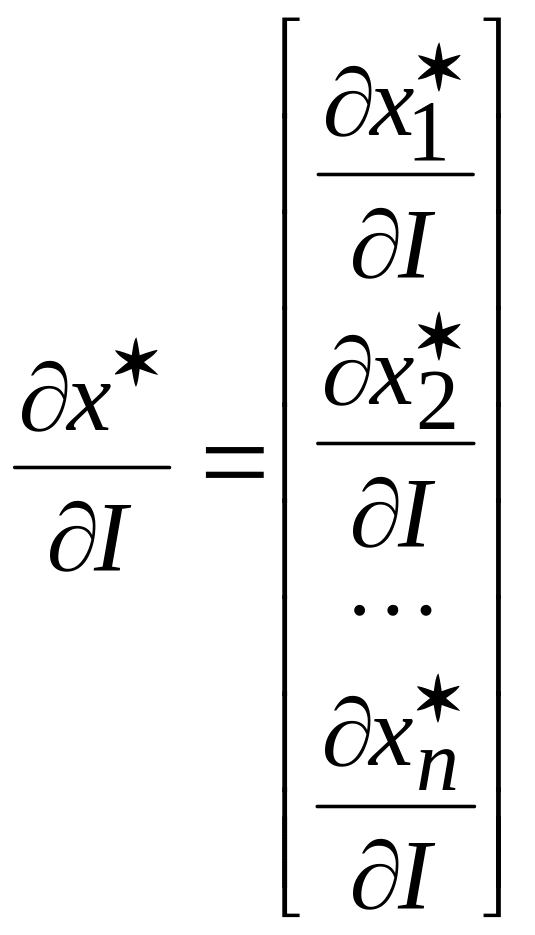
Размерность

Величины, характеризующие чувствительность спроса и предельной полезности к изменению цены р и дохода I определяются основным матричным уравнением теории полезности:

(2.25)

В (2.25) в качестве неизвестных выступают следующие величины:

матрицы: , векторы: , , . (2.26)

Общее число неизвестных – элементов указанных матриц и векторов .

Считаются неизвестными величины x^* и λ^*, т.е. матрицы правой части (2.25) и, разумеется р и Н, число элементов в матрице в правой части .

Это число- число уравнений для определения неизвестных. (2.26)

Если Н_опр определена, то из (2.25) можно получить единственное решение этого уравнения, т.е. определить величины в (2.26).

В частности из решения уравнения (2.25) следует уравнение Слуцкого

. (2.27)

Отсюда для каждого товара и цены имеем

, (2.28)

где - общий эффект изменения спроса на -й товар от изменения цены на i-й товар; - влияние компенсированного изменения спроса на товар из за изменения цены на i – ый товар;

- влияние изменения дохода на спрос на товар в зависимости от спроса на i – ый товар.

Таким образом можно записать:

общий эффект изменения спроса

= влияние компенсированного изменения цены

+ влияние изменения дохода

Можно показать, что матрица влияния замены симметричная и неотрицательно определена, т.е. для произвольной .

Из условия неотрицательности следует, что

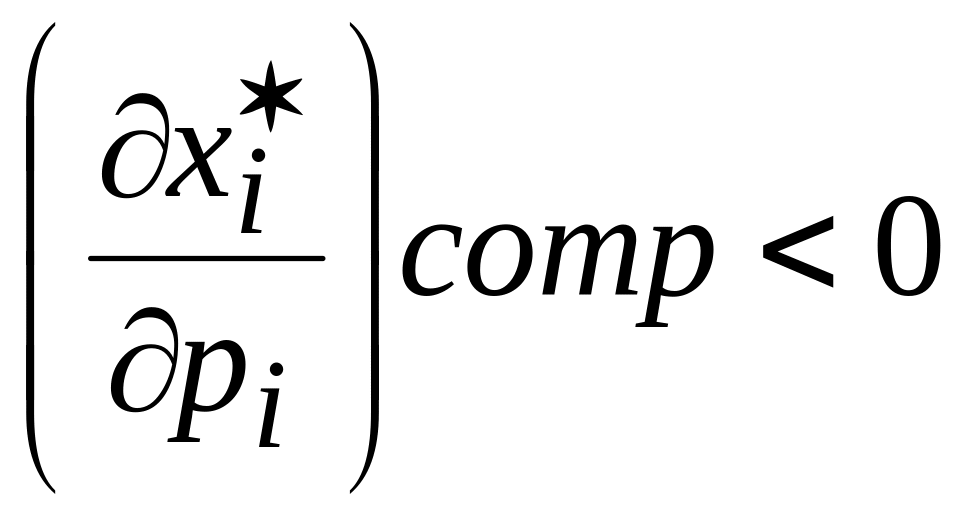, (2.29)

Это означает, что компенсированное возрастание цены товара приводит к уменьшению спроса на него: цена возросла, чтобы полезность не изменилась надо покупать меньше товара. (А чтобы компенсировать нехватку товара надо покупать тот товар, на который цена уменьшилась).

Из (2.28) имеем для j-го товара и цены на него.

Отсюда 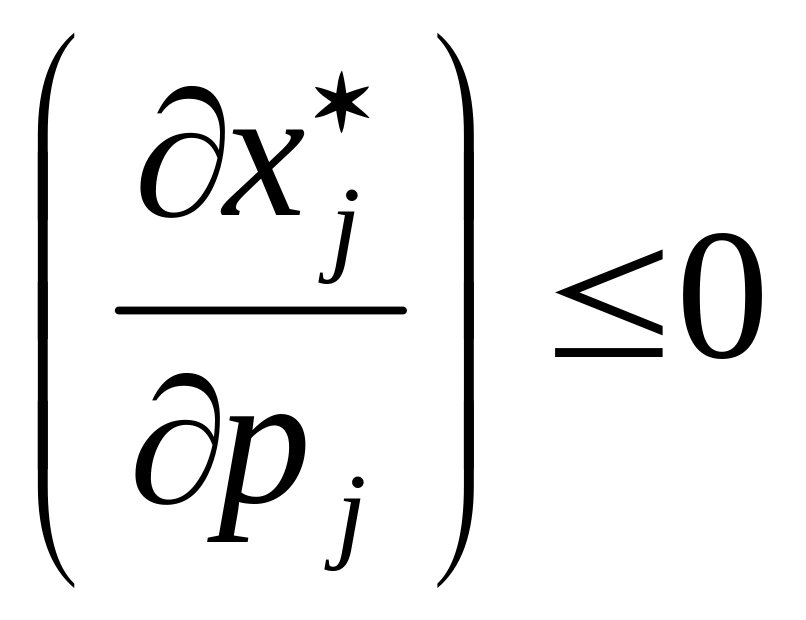, если

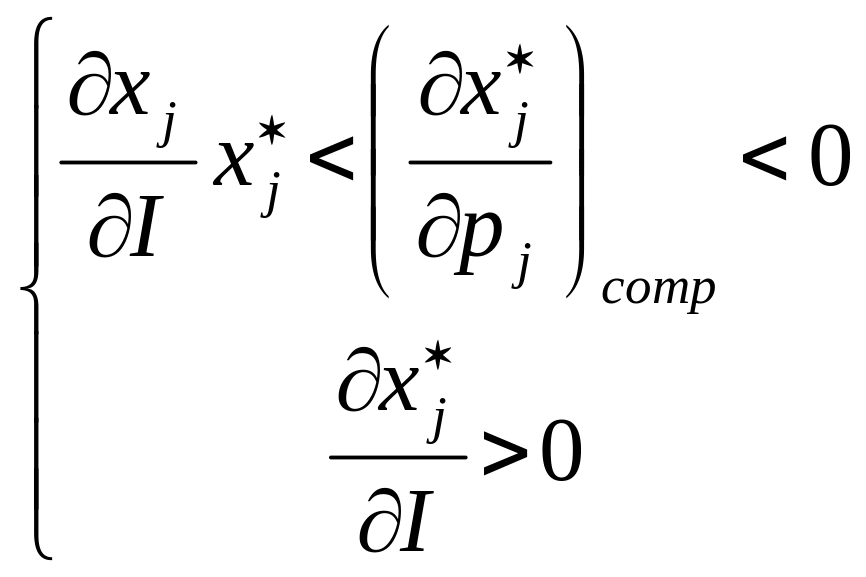
В общем случае каждый товар может быть отнесен к одной из трех категорий (табл.2.1):

Таблица 2.1

Влияние изменения цены	Влияние изменения дохода
	(ценные товары)	(малоценные товары)
Нормальные товары	Например, масло	Например, маргарин
Товары Гиффина	―	Субпродукты для малообеспеченных