3.3. Несовершенная конкуренция. Монополия и монопсония

Предыдущий раздел был построен на классическом предложении о совершенной конкуренции, т.е., что заданы цена продукции и цены ресурсов. Эти цены не зависят от объема производства фирмы, она на них не влияет. Однако во многих случаях фирма обладает некоторой монополией оказывать влияние на цену продукции, а монопсония оказывает влияние на цены затрат.

Монополист влияет на цену продукции путем варьирования выпуска продукции.

(3.20)

В общем случае фирма может снизить цену, чтобы продать больше продукции, поэтому:

(3.21)

Общий доход согласно (3.12)

(3.22)

Монополист может повлиять на цену затрат варьированием своих закупок.

(j - вид затрат)

Вообще фирма, может покупать большее количество данного ресурса, предложив более высокую плату за него:

но могут быть и скидки, если товар в избытке, тогда

.

Задача фирмы в условиях несовершенной конкуренции:

, (3.23)

где максимум берется по и ресурсам .

Функция Лагранжа

Необходимые условия минимума

(3.24)

Откуда получаем, что оптимальные значения и соответствующие условию равновесия:

↑ ↑

предельный продукт по j-ому предельная стоимость j-ого

виду затрат вида затрат

где

3.4. Конкуренция среди немногих. Олигополия и олигопсония.

Рыночный механизм, когда действует немного фирм, называется конкуренция среди немногих. Случай, когда имеется несколько продавцов продукции, называется олигополией, а когда имеется несколько покупателей определенного вида ресурса – олигопсонией. Определяющим свойством конкуренции среди немногих является то, что все конкурирующие фирмы могут влиять на цены продукции или ресурсов. Т.о., прибыль каждой фирмы зависит от политики других конкурирующих фирм. Поэтому для того, чтобы определить свою оптимальную политику, каждая фирма должна учитывать не только свое прямое влияние на рынок продукции и ресурсов, но и косвенное влияние через взаимодействие своих конкурентов.

В случае двух конкурентов каждый производит продукцию в соответствии с ПФ:

, (3.25)

где - n-мерные векторы затрат.

Цена продукции зависит от :

(3.26)

Цена любого вида ресурсов j определяется покупками этого вида ресурса обоими фирмами:

, (3.27)

где - компоненты x₁ и x₂.

В дуополии (частный случай олигополии) существует только два продавца товара и общий выпуск:

(3.28)

Пусть цена на продукцию зависит линейно от ее количества:

(3.29)

Стоимость затрат ресурсов (издержки производства) также будем считать линейной (общий вид см. (3.29)). Тогда

(3.30)

где с - предельные издержки (cq₁ – условно переменные расходы), d - условно постоянные расходы.

То, что одинаковы условно-переменные расходы на единицу продукции и условно-постоянные расходы, безусловно, является упрощение. Такое упрощение означает, что обе фирмы близки по технологии и организации производства.

Прибыль i-ой фирмы:

(3.31)

Максимизируем её по

, (3.32)

где - влияние выпуска продукции i-ой фирмы на выпуск продукции -ой фирмы.

Анализ дуаполии Курно основан на предпосылке, что при планировании своей работы каждый дуаполист считает, что изменения в его собственном выпуске продукции не повлияет на конкурента. Тогда стратегия Курно состоит в решении задач (3.32) для . В этом случае получаем:

(3.33)

или

(3.34)

Отсюда получаем:

(3.35)

Подставив в (3.34), получим:

(3.36)

Данное соотношение называется равновесием Курно.

Тогда цена на продукцию и её общий выпуск обоими фирмами согласно (3.28) и (3.29)

(3.37)

Этот результат обобщим на случай N фирм:

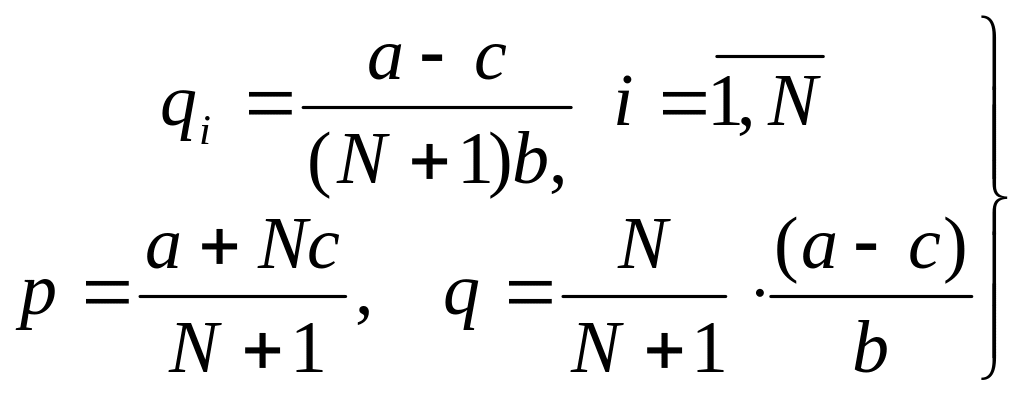(3.38)

В пределе, когда (число фирм приближенных к ) имеем из (3.38):

Экономический смысл: т.к. цена не зависит от объема производства (фирма производит бесконечно малое количество продукции и поэтому не влияет на цену товара), то при равновесие Курно стремится к равновесию к условию совершенной конкуренции.

Динамику выпуска продукции при подходе Курно, т.е. процесс перехода к состоянию (3.36), записав его так:

, т.к. получим

(3.39а)

Аналогично

(3.39б)

Выражения (3.39а) и (3.39б) представляют собой систему разностных уравнений первого порядка. Исключим из (3.39а) , подставим эту величину из (3.39б) и получим:

(3.40)

Характеристическое уравнение для (3.40) .

Корни характеристического уравнения лежат внутри единичного круга, поэтому система устойчивая. Частным решением является

,

т.к. при подставлении в (3.40) это уравнение обратится в тождество. В силу устойчивости (3.40)

,

Это подтверждает устойчивость динамической системы (3.39а) и (3.39б)

При более сложной стратегии фирмы, учитывается возможная реакция конкурента, т.е. допускается изменение выпуска конкурирующей фирмой в зависимости от выпуска рассматриваемой фирмой.

Примером служит анализ Стэкельберга, когда одна или обе фирмы считают, что влияние выпуска одной фирмы на выпуск другой фирмы отсутствует.

Пример. Рассмотрим ситуацию, когда фирма 1 полагает, что фирма 2 не будет учитывать влияние фирмы 1 на ее производство. Выпуск продукции фирмы 2 будет определятся (3.39б), которое в статике запишется так:

(3.41)

Отсюда .

Подставив эту производную в формулу (3.32), получим для :

Отсюда получаем

(3.42)

Если фирма 2 на самом деле не будет учитывать влияния фирмы 1 на ее производство, то ее выпуск будет определен (3.41). Подставив (3.41) в (3.42),получим

(3.43)

(3.44)

В рассматриваемой ситуации фирма 1 получает прибыль больше чем фирма 2. Выражение (3.43) и (3.44) называется равновесие Стэкельберга для первой фирмы. Аналогично можно записать равновесие Стэкельберга для второй фирмы:

(3.45а)

(3.45б)

Рассмотрим теперь другую ситуацию: на самом деле фирма 2 не пользуется равновесием Курно, а учитывает влияние на выпуск своей продукции выпуска фирмы 1. Иначе говоря, каждая фирма неправильно предполагает, что другая фирма не учитывает влияние на свой выпуск выпуск продукции конкурирующей фирмой. Это означает, что 1-я фирма, как и раньше, выпускает свою продукцию согласно (3.42), а фирма 2 выпускает свою продукцию по аналогичному выражению:

(3.46)

Подставив это выражение в (3.41), получаем:

(3.47)

Данное выражение называется неравновесием Стэкельберга, при котором обе фирмы получают меньшую прибыль, чем при равновесии Курно. Эта ситуация больше отвечает практике.

Все возможные ситуации представлены в виде матрицы

Данная матрица представляет собой матрицу реакций конкурентов в ответ на предполагаемый ход противника. Эта ситуация может быть рассмотрена с позиций теории игр.

Таблица 3.1

Фирма 1	Фирма 2
	Реакция Курно	Реакция Стэкельберга
Реакция Курно	Равновесие Курно (3.36); (3.36)	Равновесие Стэкельберга для 2-ой фирмы (3.45а); (3.45б)
Реакция Стэкельберга	Равновесие Стэкельберга для 1-ой фирмы (3.43);(3.44)	Неравновесие Стэкельберга (3.47); (3.47)

Кроме приведенных могут быть и другие решения. Предположим, что фирмы пришли к соглашению максимизировать общую прибыль (групповой сговор). Тогда общая прибыль согласно (3.31)

(3.48)

Из условия максимума общей прибыли получаем

Откуда следует

(3.49)

Т.о. нет однозначного решения: все выпуски, удовлетворяющие (3.49), оптимальны с точки зрения выбранного критерия (3.48). Как трактовать такое решение, смотри рис. 3.1.

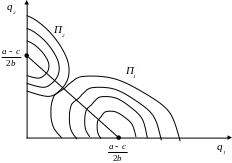
Рис. 3.1

Линии равного уровня – эллипсы (согласно (3.31)). Точки их касания на прямой, соединяющей точки максимума прибылей обеих фирм. Эти точки (на прямой) – неулучшаемые: уменьшение прибыли одной фирмы ведёт к уменьшению прибыли другой. Такие точки называются оптимальными решениями по Парего двухкритериальной задачи

, ,

когда оба критерия (обе фирмы) равноценны, о чём говорит свёртка этих критериев в один, см. (3.48). Эту прямую некоторые авторы называют договорной (или компромиссной): только договорившись фирмы смогут определить объём своего производства.