1. .Рациональное ведение хозяйства и экономики

Основной задачей экономики является рациональное ведение хозяйства, рациональная деятельность (economizing), т.е. распределение ограниченных ресурсов для достижения поставленных целей. Вследствие ограничения ресурсов приходится выбирать тот или иной вариант их использования. К задачам, связанным с рациональным ведением хозяйства относят, например, распределение дохода на цели потребления и сбережения, распределения общей суммы расходов на потребление между различными видами товаров и услуг.

Экономика в целом представляет собой совокупность определенных институтов, каждый из которых решает стоящую перед ним задачу рационального ведения хозяйства. В число таких институтов входят:

Потребители (домашние хозяйства): отдельные лица или группы лиц с общим доходом, расходуемым на потребление.

Фирмы: предприятия (единоличная собственность, аукционная общества), производящие товары и услуги.

Профессиональные союзы: группы людей, работающих по найму, организованные для того, чтобы заключать с предпринимателями коллективные договоры или выполнение определенных задач.

Правительственные организации: политические учреждения часто обладающие важными экономическими функциями.

Экономику можно рассматривать как науку о применении методов рациональной деятельности хозяйственных институтов. Таким образом, экономическая наука рассматривает распределение ограниченных ресурсов в домашнем хозяйстве, фирме и в ряде других институтов.

Следовательно, для всех перечисленных институтов может быть указана функция цели, средства (инструмент) управления, ограничения на ресурсы и нормативные правила, регулирующие, например, распределение дохода между товарами и услугами.

2.Теория потребления

2.1. Пространство товаров

Поведение потребителя, рассматриваемое с точки зрения рационального ведения хозяйства, математически выражается в выборе некоторой точки из пространства товаров. Под товаром будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, существует конечное число наличных товаров n, количества каждого из них, потребленные потребителем, характеризуются набором товаров x

, (2.1)

где , j= - количество j-го блага приобретенного некоторым потребителем.

С целью упрощения будем считать, что может быть куплено любое неотрицательное количество блага (товара). Тогда все возможные наборы товаров являются векторами пространства товаров , т. е. , = .

Т.о, С- неотрицательный ортант в -мерном пространстве (замкнутое и выпуклое множество).

2.2. Отношение предпочтения

Выбор потребителем некоторого набора товаров отчасти зависит от его вкусов. Они характеризуются слабым отношением предпочтения, либо слабым предпочтением: «предпочтительнее чем» или «равноценен», которое записывается далее как « ».

Следовательно, запись

, (2.2)

где x и y – наборы товаров (точки пространства С), означает, что рассматриваемый потребитель либо предпочитает набор x набору y, либо не делает между ними различий: x по крайней мере так же хорош как и у.

Определим теперь понятие безразличия. Наборы товаров x и y безразличны для потребителя (x~y) тогда и только тогда, когда каждый предпочтительнее или безразличен по отношению к другому, т. е.

x~y, если и только если x y и y x (2.3)

Потребитель предпочитает набор х набору у (x y), если и только если х предпочтительнее или безразличен у, а у не предпочтительнее или не безразличен х:

х у, если и только если x y, а отношение y x неверно (2.4)

Отношение в пространстве товаров называется совершенным, если для любых наборов товаров х и у из С справедливо:

либо x y, либо y x, либо (x y и y x одновременно) (2.5)

Соотношение (2.5) означает, что в С нет «пробелов», в которых предпочтения не существует.

Отношение называется транзитивным (полуупорядоченным), если, для любых трех наборов х, у и z из С выполняется условие:

если x y, у z, то х z (2.6)

Отношение называется рефлексивным, если х x.

Отношение называется симметричным, если x y влечёт y x.

Рассмотрим две основные аксиомы о слабом отношении предпочтения.

Аксиома 1. Слабое отношение предпочтения является совершенной полуупорядоченностью пространства товаров С.

Аксиома утверждает, что для произвольных х и у в С справедливы формулы (2.5), (2.6). Из аксиомы 1 можно получить следующие свойства отношений эквивалентности. Это отношение:

• транзитивно: если x~y, у~z, то x~z;

• рефлексивно: x~х (любой набор товаров эквивалентен сам себе)

• симметрично: x~y означает у~х.

Отношение безразличия делит пространство товаров С на классы эквивалентности, называемые множествами безразличия, каждое из которых состоит из всех наборов, безразличных заданному набору х.

Сказанное можно записать так: множество безразличия для товара х:

(2.7)

Введем понятие предпочтительного и непредпочтительного множеств.

Предпочтительное множество – множество, состоящее из наборов товаров, которые предпочитаются или безразличны заданному набору х.

(2.8)

Непредпочтительное множество – множество, которое состоит из тех наборов товаров, для которых х предпочтительнее или безразличен:

(2.9)

Аксиома 2. Слабое отношение предпочтения непрерывно.

Согласно аксиоме 2 отношение предпочтения непрерывно, т.е. предпочтительные множества и непредпочтительные множества являются замкнутыми множествами в пространстве С, т.е. содержат свои граничные точки. Причём

(2.10)

Формула (2.10) означает пересечение множества предпочтения с множеством непредпочтения.

Из двух основных аксиом совершенной полуупорядоченности и непрерывности, следует, что существует непрерывная функция вектора товаров х , которую обозначим . Функция называется фунуцией полезности. Для нее справедливо:

u(x) u(y), только если (2.11)

Будем считать u(x) дифференцируемой и такой, что градиент функции u(x) положителен:

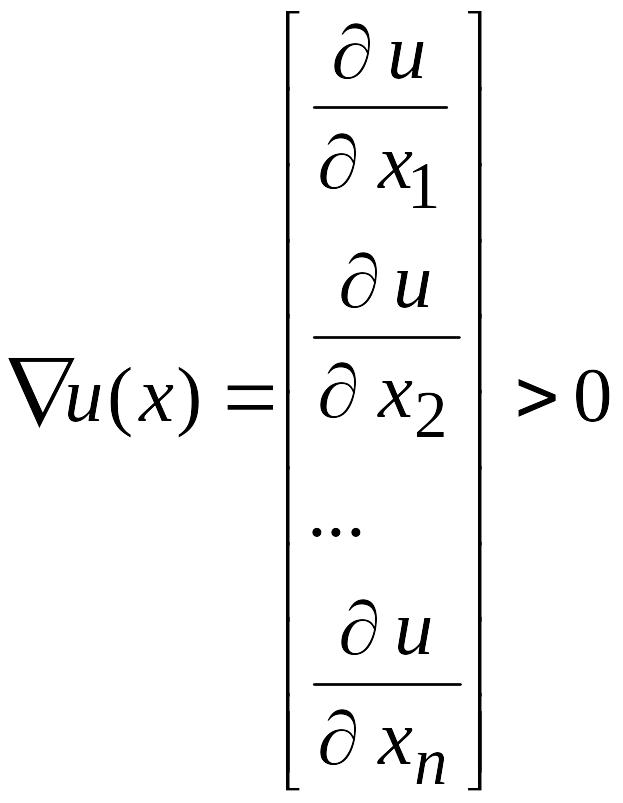(2.12)

Соотношение (2.12) означает, что все частные производные , i= , т.е. с увеличением количества товаров, функция полезности увеличивается.

Частные производные , , называются предельными полезностями.

Далее рассмотрим аксиому строгой выпуклости. Пусть х и у – различные наборы товаров в С, причем , тогда

. (2.13)

Согласно (2.8) и (2.13)

На рис. 2.1 изображено множество предпочтений , удовлетворяющее этой аксиоме соответственно для n=1, 2.

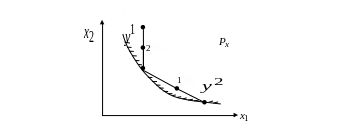
Рис.2.1. Точка 1 определяется выражением , точка 2 - выражением

На рис.2.1 граница множества - представляет собой множество безразличия , которое представляет собой кривую безразличия. Как видно из рис.2.1 множество - строго выпуклое. Тогда можно показать, что множество

, (2.14)

также выпуклое для любого вещественного а.

Рассмотрим в качестве примера рис. 2.2. На нем изображено для (пространство товаров - одномерное) множество , которое представляет собой заштрихованную часть числовой оси (оси -ов). Из рис.2.2 видно, что множество выпуклое для любого а.

Для иллюстрации вида множества в двумерном случае (размерность пространства товаров ) нам понадобится понятие линии равного уровня функции с числом переменных больше единицы.

Будем рассекать эту функцию плоскостями, параллельными координатной плоскости . Спроектируем линии пересечения функции с плоскостями на координатную плоскость, см. рис. 2.2.

Рис.2.2

Рис.2.3

Эти проекции наываются линиями равного уровня. На каждой такой линии значение функции полезности одинаковое. На рис. 2.3 приведены кривые для значений .

Кривая безразличия представляет собой линию равного уровня для функции . Без потери общности будем считать, что , где величина фигурирует в формуле (2.14). В силу свойства строгой выпуклости имеет место следующие неравенства . Множество представляет собой заштрихованную на рис. 2.3. область. Как видно, эта область – выпуклая.

Предположим, что – дважды непрерывно дифференцируемая функция и матрица ее вторых производных (матрица Гессе) отрицательно определена. Это означает, что для любого ненулевого - мерного вектора выполняется неравенство: . Отрицательно определеная матрица часто обозначается так: . В нашем случае, - матрица Гессе имеет вид:

.

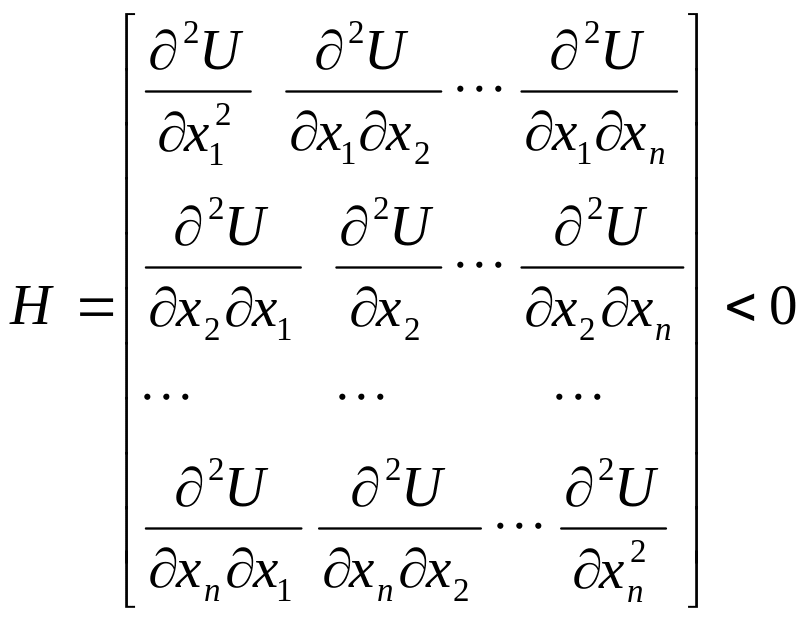Матрица Н – симметричная. Отрицательная определенность матрицы Н вместе с условием (2.14) означает , что строго вогнутаяфункция. Отсюда следует, что элементы на главной диаганали - отрицательные, т.е.

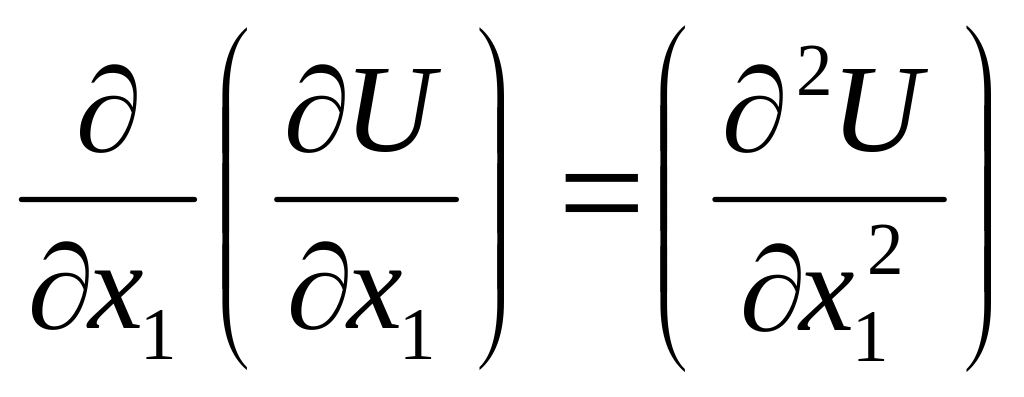< 0 (2.15)

Из формулы (2.15) следует, что скорость изменения первой производной - предельной полезности – отрицательная. Таким образом, формула (2.15) означает, что предельная полезность любого товара уменьшается по мере того, как он потребляется. Допущение об отрицательной определености матрицы , которое влечет (2.15), называется законом Госсена.

Примеры функций полезности.

1. Квадратическая:

, , , ,

где - транспонированный вектор, - заданные величины.

2. Логарифмическая (Бернулли):

,

где - заданные величины.

3. Постоянной эластичности:

, >0, 0 < < 1, > >0, .

Величины - заданы.