17. Многочлены от одной переменной. Степень многочлена. Равные многочлены. Основные свойства операций сложения и умножения многочленов.

Многочлен с одной переменной – это многочлен вида: , где - коэффициенты, а х – переменная.

Многочлен ax + b , где a= =0, a, b - числа, x - переменная, называется многочленом первой степени .  Многочлен ax2+bx+c, где a= =0, a , b , c - числа, x - переменная, называется многочленом второй степени ( квадратным трёхчленом , квадратичной функцией ).  Многочлен ax3+bx2+cx+d, где a= =0, a , b , c , d - числа, x - переменная, называется многочленом третьей степени .

Вообще, многочлен P _n ( x ) = a _n x ⁿ + a _{n – 1} x ^{n – 1} + a _{n – 2} x ^{n – 2} + ... + a ₁ x + a ₀ , где a= =0,ak k=0 1 2 3 n - числа, x - переменная, называется многочленом n -ной степени .  Традиционно an называется старшим коэффициентом , а a0 - свободным членоммногочлена

Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени.  Описать формулы сокращенного умножения. Как складывать и вычитать. Как умножать многочлена и т.д.

18. Деление многочленов с остатком.

Пусть даны 2 многочлена Pn(x) and Qk(x) ((n>k)) Если существует многочлен Se(x), такой что имеет место — (делимое)Pn(x)=(делитель)Qk(x)*(частное)Se(x), то говорят, что Pn(x) нацело делится на Qk(x), где k+e=n

Для многочленов Pn(x) и Qk(x) существует единственная пара многочленов Se(x) и Rm(x), таких что выполнено : Pn(x)(делимое) = Qk(x)(делитель) * Se(x)(неполное частное) +Rm(x)(остаток), где m < k

19) Значение многочлена. Корень многочлена. Теорема Безу и её важнейшее следствие.

Корень многочлена — корень уравнение, которое получится если многочлен приравнять к нулю.

Остаток от деления многочлена P(x) на двучлен (x-c) равен значению многочлена при x=c.

Докозательство. P(x) = (x-c) * S(x) +R(x)

P(c) = (c-c)*S(c) +R R = P(c)

Следствие.  Если число С является корнем многочлена, то этот многочлен без остатка делится на (x-c)

20. Схема Горнера

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корнимногочлена[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида x − c. Метод назван в честь Уильяма Джорджа Горнера (англ.).

Описание алгоритма

Задан многочлен P(x):

 .

Пусть требуется вычислить значение данного многочлена при фиксированном значении x = x0. Представим многочлен P(x) в следующем виде:

 .

Определим следующую последовательность:

…

…

Искомое значение P(x0) = b0. Покажем, что это так.

В полученную форму записи P(x) подставим x = x0 и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через bi:

21.Рациональные корни многочленов с целыми коэффициентами.

Если многочлен   с целыми коэффициентами имеет рациональный корень   то число p является делителем числа   (свободного члена), а число q является делителем числа   (старшего коэффициента).

Доказательство :  

Действительно, если число   является корнем многочлена   то   а именно:   Умножим обе части этого уравнения на   получим: 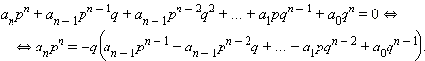  Так как   − целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q , так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q , так как она равна правой. Число p не делится на q , так как иначе дробь   была бы сократимой, значит и   не делится на q . Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно   Аналогично доказывается, что   делится на p . Теорема доказана.