11) Асимптоты (вертикальные, наклонные)графика функции, вывод правила их нахождения.

Вертикальная

Вертикальная асимптота — прямая вида    при условии существования предела   .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Наклонная

Наклонная асимптота — прямая вида    при условии существования пределов

1.

2.

 Наклонная пример.

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен   ), то наклонной асимптоты при   (или   ) не существует!

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов 

3. Нахождение двух пределов   :

если    в п. 2.), то   , и предел    ищется по формуле горизонтальной асимптоты,   .

12) Определение комплексных чисел.

Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается   . Любое комплексное число может быть представлено как формальная сумма x+iy, где x и y — вещественные числа, i— мнимая единица

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней (основная теорема алгебры).

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z2 + 1 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел   , как и любые другие конструкции поля разложения многочлена z2 + 1.

Алгебраическая форма

Запись комплексного числа z в виде x + iy,   , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1):

(a + ib) + (c + id) = (a + c) + i(b + d);

Сопряжённые комплексные числа

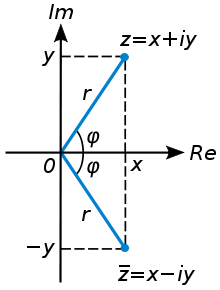
Геометрическое представление сопряжённых чисел

Если комплексное число z = x + iy, то число    называется сопряжённым (или комплексно сопряжённым) к z (обозначается также z * ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

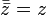•   (сопряжённое к сопряжённому есть исходное).

• 

• 

• 

• 

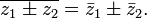
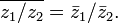
Обобщение:   , где p(z) — произвольный многочлен с вещественными коэффициентами.

• 

• 

Значимость сопряжения объясняется тем, что оно является образующей группы Галуа   .

Модуль и аргумент

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа z обозначается | z | и определяется выражением   . Часто обозначается буквами    или   . Если z является вещественным числом, то | z | совпадает с абсолютной величиной этого вещественного числа.

Для любых    имеют место следующие свойства модуля. :

1)   , причём    тогда и только тогда, когда   ;;

2)    (неравенство треугольника);

3)   ;

4)   .

Из третьего свойства следует   , где   . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем   .

5) Для пары комплексных чисел z1 и z2 модуль их разности | z1 − z2 | равен расстоянию между соответствующими точками комплексной плоскости.

Угол    (в радианах) радиус-вектора точки, соответствующей числу z, называется аргументом числа z и обозначается   .

• Из этого определения следует, что   ;   ;   .

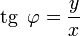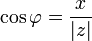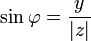• Для комплексного нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2kπ, где k — любое целое число.

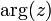• Главным значением аргумента называется такое значение   , что   . Часто главное значение обозначается   [4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: