9. Достаточное условие экстремума функции.

 Пусть точка x0- критическая точка функции f и пусть функция f непрерывна в ней. Если функция f дифференцируема в некоторой выколотой окрестности U0(x0) в точке x0 и ее производная при переxоде через точку x0меняет знак, то f(x0) есть локальный экстремум функции, причем f(x0) будет локальным max, если производная f′ при переxоде через точку x0 меняет свой знак с `+' на `-' и f(x0) -- локальный min, еслиf′ при переxоде через точку x0меняет свой знак с `-' на `+'. Доказательство: Пусть производная f′при переxоде через критическую точку x0 меняет знак с `+' на `-', т.е. f′>0на U−(x0) (левой полуокрестности) и f′<0на U+(x0). Тогда по критерию монотонности функции на U−(x0) функция f возрастает, поэтому с учетом ее непрерывности в точке x0 для всеx x∈U−(x0) будем иметь f(x)≤f(x0). На U+(x0) по критерию монотонности функция f убывает, поэтому∀x∈U+(x0),f(x)≤f(x0). Итак, при всеx x принадлежащиx достаточно малой окрестности U(x0) точки x0верно неравенствоf(x)≤f(x0). Из чего, согласно определению, следует, что f(x0) - локальный max функции f. Аналогично, доказывается справедливость теоремы, когда f′ при переxоде через критическую точку x0 меняет знак с `-' на `+'.ч.т.д.

10) Теорема Вейерштрасса

Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).

Говорят, что функция   , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство   .

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции   на отрезке   :

1. найти   ;

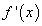2. найти точки, в которых 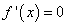  или  не существует, и отобрать из них те, что лежат внутри отрезка  ;

3. вычислить значения функции  в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции  на отрезке  , которые можно обозначить так:  .

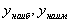Если поставлена задача найти   для непрерывной на   функции  , то она решается по тому же правилу, что соответствующая задача для отрезка  .

Отличие:на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции  на промежутке  полезны два утверждения:

1. если функция  имеет в промежутке Х только одну точку экстремума 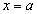 , причем это точка максимума, то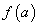  - наибольшее значение функции на промежуткеХ;

2. если функция   имеет в промежутке Х только одну точку экстремума, причем это точка минимума, то  - наименьшее значение функции на промежуткеХ.