
- •1) Определение предела функции в точке. Предел суммы, произведения, частного двух функций.
- •2) Определение производной, её геометрический и физический смысл. Определение касательной к графику функции. Вывод уравнения касательной к графику функции.
- •3) Теорема о непрерывности дифференцируемой функции.
- •4) Правила Дифференцирования.
- •Понятие сложной функции. Правило вычисления производной сложной функции.
- •7) Определение монотонной функции. Достаточное условие монотонности функции на промежутке .
- •8) Экстремум функции
- •Достаточное условие экстремума функции.
- •10) Теорема Вейерштрасса
- •11) Асимптоты (вертикальные, наклонные)графика функции, вывод правила их нахождения.
- •12) Определение комплексных чисел.
- •13) Операции над комплексными числами в алгебраической форме и их свойства.
- •14) Геометрическая интерпретация комплексного числа
- •16) Определение комплексного корня n-й степени из комплексного числа
- •Многочлены от одной переменной. Степень многочлена. Равные многочлены. Основные свойства операций сложения и умножения многочленов.
- •Деление многочленов с остатком.
- •19) Значение многочлена. Корень многочлена. Теорема Безу и её важнейшее следствие.
- •21.Рациональные корни многочленов с целыми коэффициентами.
- •22.Обобщенная теорема Виета для многочленов n-ой степени
- •23.Векторы в пространстве. Сумма и разность векторов, умножение вектора на число. Коллинеарные векторы. Компланарные векторы. Угол между векторами.
- •26.Определение скалярного произведения двух векторов и его свойства.
- •27.Различные виды уравнения плоскости
- •28.Определение угла между плоскостями. Формула вычисления кос угла между плоскостями с выводом
- •29.Различные виды уравнений прямой в пространстве
- •30.Взаимное расположение прямой и плоскости
- •31.Вычисление координат точки пересечения прямой с плоскостью
- •32.Определение расстояния от точки до плоскости
- •33.Уравнение сферы…
1) Определение предела функции в точке. Предел суммы, произведения, частного двух функций.
Функция ![]() имеет
предел
имеет
предел ![]() в
точке
в
точке ![]() , предельной для
области определения функции
,
если для каждой окрестности
предела
существует
проколотая окрестность точки
,
образ которой при отображении
является
подмножеством заданной окрестности
точки
.
, предельной для
области определения функции
,
если для каждой окрестности
предела
существует
проколотая окрестность точки
,
образ которой при отображении
является
подмножеством заданной окрестности
точки
.
Предел суммы равен сумме пределов:
![]()
Предел произведения равен произведению пределов:
![]()
Предел частного равен частному пределов.
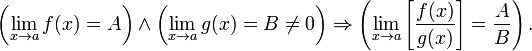
2) Определение производной, её геометрический и физический смысл. Определение касательной к графику функции. Вывод уравнения касательной к графику функции.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Пусть
в некоторой окрестности точки![]() определена
функция
определена
функция ![]() Производной
функции называется такое число
,
что функцию в окрестности U(x0)
можно представить в виде f(x0
+ h)
= f(x0)
+ Ah + o(h),
если
существует.
Производной
функции называется такое число
,
что функцию в окрестности U(x0)
можно представить в виде f(x0
+ h)
= f(x0)
+ Ah + o(h),
если
существует.
Определение через предел:
![]()
Геометрический смысл производной. Тангенс угла наклона касательной прямой
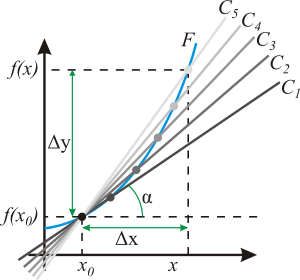
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Если
функция ![]() имеет
конечную производную в точке x0,
то в окрестности U(x0)
её можно приблизить линейно йфункцией
имеет
конечную производную в точке x0,
то в окрестности U(x0)
её можно приблизить линейно йфункцией
![]()
Функция fl называется
касательной к f в
точке x0.
Число ![]() является
угловым
коэффициентом или тангенсом угла
наклона касательной
прямой.
является
угловым
коэффициентом или тангенсом угла
наклона касательной
прямой.
Физический смысл производной. Скорость изменения функции
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) =s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражаетмгновенное ускорение в момент времени t0.
Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
Вы ведем
уравнение касательной.
ведем
уравнение касательной.
Y= kx+b
k=tgA(альфа) k=tgA=f'(x0)
Смотрим на картинку.
(x0;f(x0))-принадлежит прямой
f(x0)=f'(x0)x0+b =>b=f(x0)-f'(x0)x0
Таким образом...
y=f'(x0)x+f(x0)-f'(x0)x0
y=f'(x0)+f'(x0)(x-x0) – уравнение касательной к графику f(x) в точке x.
3) Теорема о непрерывности дифференцируемой функции.

4) Правила Дифференцирования.
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если С— постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующиеправила дифференцирования:
C' = 0
x' = 1
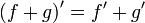

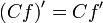
 (g≠0)
(g≠0) (g≠0)
(g≠0)
