
- •1) Определение предела функции в точке. Предел суммы, произведения, частного двух функций.
- •2) Определение производной, её геометрический и физический смысл. Определение касательной к графику функции. Вывод уравнения касательной к графику функции.
- •3) Теорема о непрерывности дифференцируемой функции.
- •4) Правила Дифференцирования.
- •Понятие сложной функции. Правило вычисления производной сложной функции.
- •7) Определение монотонной функции. Достаточное условие монотонности функции на промежутке .
- •8) Экстремум функции
- •Достаточное условие экстремума функции.
- •10) Теорема Вейерштрасса
- •11) Асимптоты (вертикальные, наклонные)графика функции, вывод правила их нахождения.
- •12) Определение комплексных чисел.
- •13) Операции над комплексными числами в алгебраической форме и их свойства.
- •14) Геометрическая интерпретация комплексного числа
- •16) Определение комплексного корня n-й степени из комплексного числа
- •Многочлены от одной переменной. Степень многочлена. Равные многочлены. Основные свойства операций сложения и умножения многочленов.
- •Деление многочленов с остатком.
- •19) Значение многочлена. Корень многочлена. Теорема Безу и её важнейшее следствие.
- •21.Рациональные корни многочленов с целыми коэффициентами.
- •22.Обобщенная теорема Виета для многочленов n-ой степени
- •23.Векторы в пространстве. Сумма и разность векторов, умножение вектора на число. Коллинеарные векторы. Компланарные векторы. Угол между векторами.
- •26.Определение скалярного произведения двух векторов и его свойства.
- •27.Различные виды уравнения плоскости
- •28.Определение угла между плоскостями. Формула вычисления кос угла между плоскостями с выводом
- •29.Различные виды уравнений прямой в пространстве
- •30.Взаимное расположение прямой и плоскости
- •31.Вычисление координат точки пересечения прямой с плоскостью
- •32.Определение расстояния от точки до плоскости
- •33.Уравнение сферы…
30.Взаимное расположение прямой и плоскости
Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпердикулярна и самой наклонной.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, расположенной в этой плоскости, то она параллельна этой плоскости.
Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости.
Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Все точки прямой, параллельной плоскости, одинаково удалены от этой плоскости.
1. Если прямые
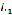 и
и 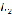 заданы
общими уравнениями
заданы
общими уравнениями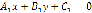 и
и 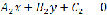 ,
,тогда угол между ними равен углу между их нормалями, то есть между векторами
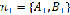 и
и 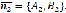
Следовательно,
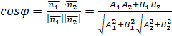 .
.Условия параллельности и перпендикулярности прямых тоже сводятся к условиям параллельности и перпендикулярности нормалей:
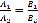 – условие
параллельности прямых
и
;
– условие
параллельности прямых
и
; – условие
перпендикулярности прямых
и
.
– условие
перпендикулярности прямых
и
.2. Если прямые и заданы каноническими уравнениями
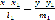 и
и 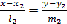 ,
,где
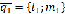 и
и 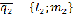 направляющие
векторы прямых
и
, то
по аналогии с пунктом 1 получим:
направляющие
векторы прямых
и
, то
по аналогии с пунктом 1 получим: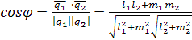 ,
,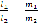 – условие
параллельности прямых
и
– условие
параллельности прямых
и 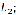
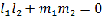 – условие
перпендикулярности прямых
и
.
– условие
перпендикулярности прямых
и
.
Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.
31.Вычисление координат точки пересечения прямой с плоскостью
32.Определение расстояния от точки до плоскости
Расстояние
от точки до плоскости --- это наименьшее
из расстояний между этой точкой и точками
плоскости. Известно, что расстояние от
точки до плоскости равно длине
перпендикуляра, опущенного из этой
точки на плоскость. Если плоскость
задана уравнением ![]() , то
расстояние
, то
расстояние ![]() от
точки
от
точки ![]() до
этой плоскости можно вычислить по
формуле
до
этой плоскости можно вычислить по
формуле
![]() .
.
Математически верная формулировка
![]() (где
(где ![]() ---
расстояние от точки с координатами
---
расстояние от точки с координатами ![]() до
плоскости
).
до
плоскости
).
Доказательство. Расстояние
от точки ![]() до
плоскости
до
плоскости ![]() -- это,
по определению, длина перпендикуляра
-- это,
по определению, длина перпендикуляра ![]() , опущенного
из точки
на
плоскость
(рис. 11.9).
, опущенного
из точки
на
плоскость
(рис. 11.9).
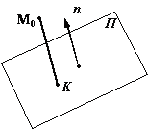
Рис.11.9.Расстояние от точки до плоскости
Вектор ![]() и
нормальный вектор n плоскости
параллельны,
то есть угол
и
нормальный вектор n плоскости
параллельны,
то есть угол ![]() между
ними равен 0 или
между
ними равен 0 или ![]() , если
вектор n имеет
направление противоположное, указанному
на рис. 11.9. Поэтому
, если
вектор n имеет
направление противоположное, указанному
на рис. 11.9. Поэтому
![]()
Откуда
|
(11.8) |
Координаты
точки ![]() , которые
нам неизвестны, обозначим
, которые
нам неизвестны, обозначим ![]() . Тогда
. Тогда ![]() . Так
как
. Так
как ![]() , то
, то ![]() . Раскрыв
скобки и перегруппировав слагаемые,
получим
. Раскрыв
скобки и перегруппировав слагаемые,
получим
|
(11.9) |
Точка
лежит
на плоскости
, поэтому
ее координаты удовлетворяют уравнению
плоскости: ![]() . Отсюда
находим, что
. Отсюда
находим, что ![]() .Подставив
полученный результат в
формулу (11.9), получим
.Подставив
полученный результат в
формулу (11.9), получим ![]() . Так
как
. Так
как ![]() , то
из формулы (11.8) следует
формула (11.7).
, то
из формулы (11.8) следует
формула (11.7).

