39.Основные схемы кулачковых механизмов. (Билет 40) Методы замыкания кулачковых механизмов. Схемы замыкания.

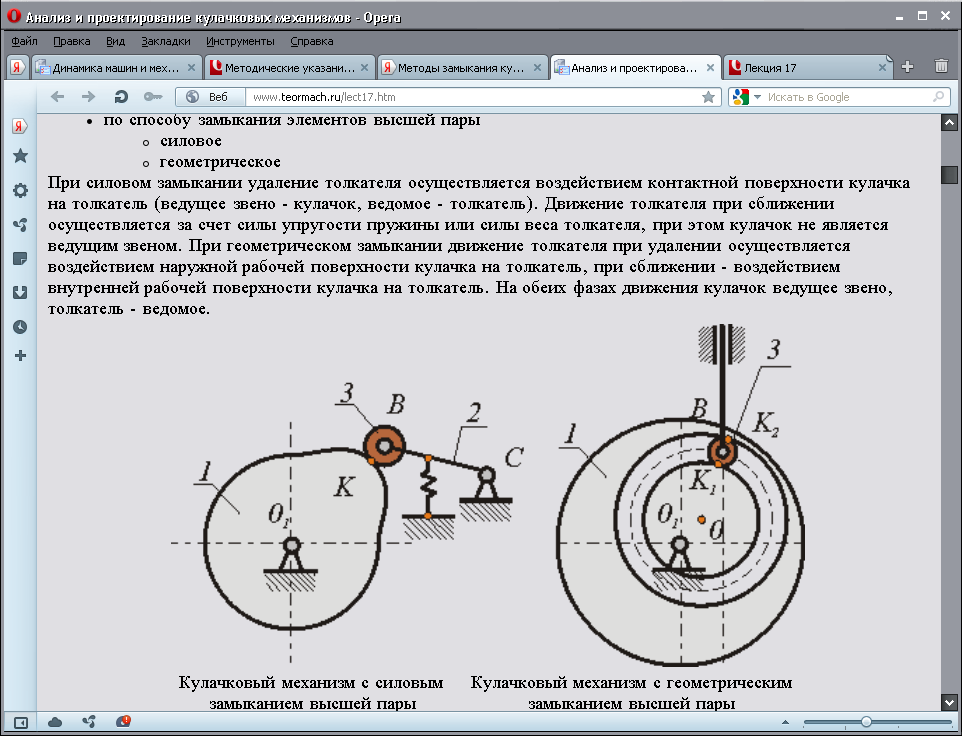
40.Кулачковые механизмы. Виды кулачковых механизмов и их особенности.

Кулачковым называется трехзвенный механизм с высшей кинематической парой входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено - ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью.

Кулачковые механизмы являются одними из наиболее распространенных устройств в различных приводах и машинах: в силовых приводах станков-автоматов, в приводах перемещения резцов и столов зубострогальных и зубодолбёжных станков, в клапанных механизмах поршневых насосов, компрессоров, газораспределения ДВС и т.д.

В связи с широким применением кулачковые механизмы конструктивно весьма разнообразны. В них используются кулачки : плоские, с поступательным перемещением; цилиндрические; дисковые; конические; гиперболоидные; коноидные.

Применяемые толкатели 2 разделяются (рис.15.1):

— по виду совершаемого движения: с поступательным движением (схемы ); с вращательным движением (схемы ), называемый коромысловым;

— по форме рабочей поверхности башмака, контактирующего с кулачком 1:

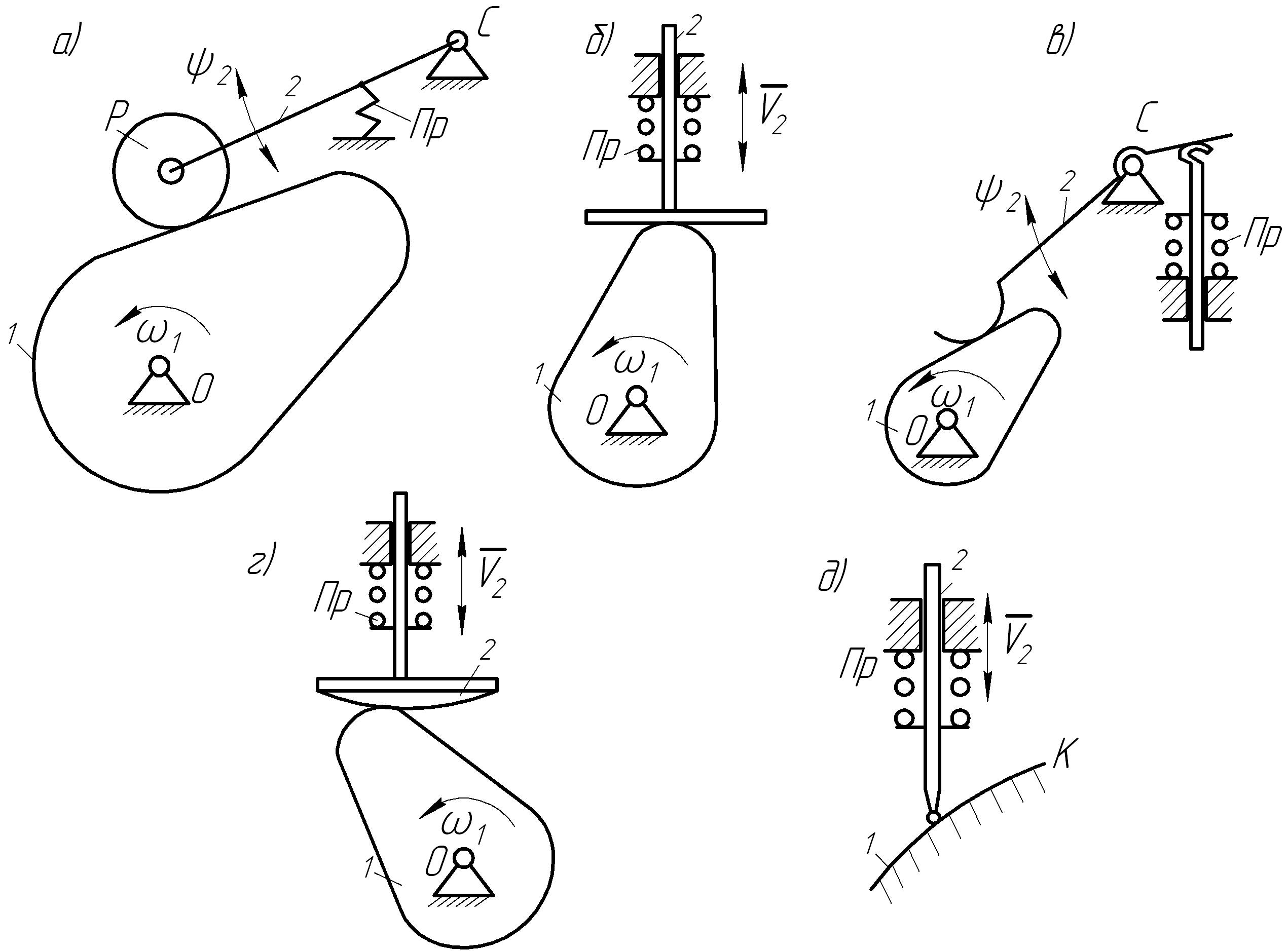
Рис. 15.1. Основные виды толкателей 2:

– роликовый; – тарельчатый плоский; – цилиндрический;

– тарельчатый сферический; – остроконечный сферический.

Выполнение башмака в виде ролика Р (на схеме ) частично исключает трение скольжения, заменяя его трением качения, уменьшает износ и повышает надёжность механизма. Уменьшение износа обеспечивается также применением для кулачков и башмаков толкателей: сталей марок 45, 40Х с закалкой до твёрдостей 52…58HRC; сталей 15, 20Х, 25ХГ с цементацией и закалкой до 56…62HRC; высокопрочных чугунов. При работе механизма необходим постоянный контакт кулачка с башмаком толкателя. Он может обеспечиваться:

— силовым замыканием кулачковой пары посредством пружины ПР (рис.15.1), давления жидкости или воздуха и т.п.;

— геометрическим замыканием с использованием (рис. 15.2):

) пазового кулачка ) парного кулачка 1 и сдвоенного толкателя 2

41.Планетарные зубчатые механизмы. Выбор схемы, числа сателлитов и чисел зубьев колёс.

Выбор схем планетарных механизмов

Планетарные механизмы позволяют получить большие передаточные отношения, имея при этом значительно меньшие габариты и в 1,5…3,0 раза меньшую массу по сравнению со ступенчатыми механизмами одинакового передаточного отношения.

Заданное передаточное отношение обеспечивается различными существующими схемами планетарных механизмов, но они могут значительно отличаться по КПД, массе и габаритам. По этим качествам простые планетарные механизмы разделяются на две группы:

1. Схемы механизмов первой группы приведены на рис. 14.2. Они выполнены двухрядными, имеют двойные сателлиты 2,3, составлены из колёс однотипного зацепления - только внешнего (схема ) или только внутреннего (схема ).

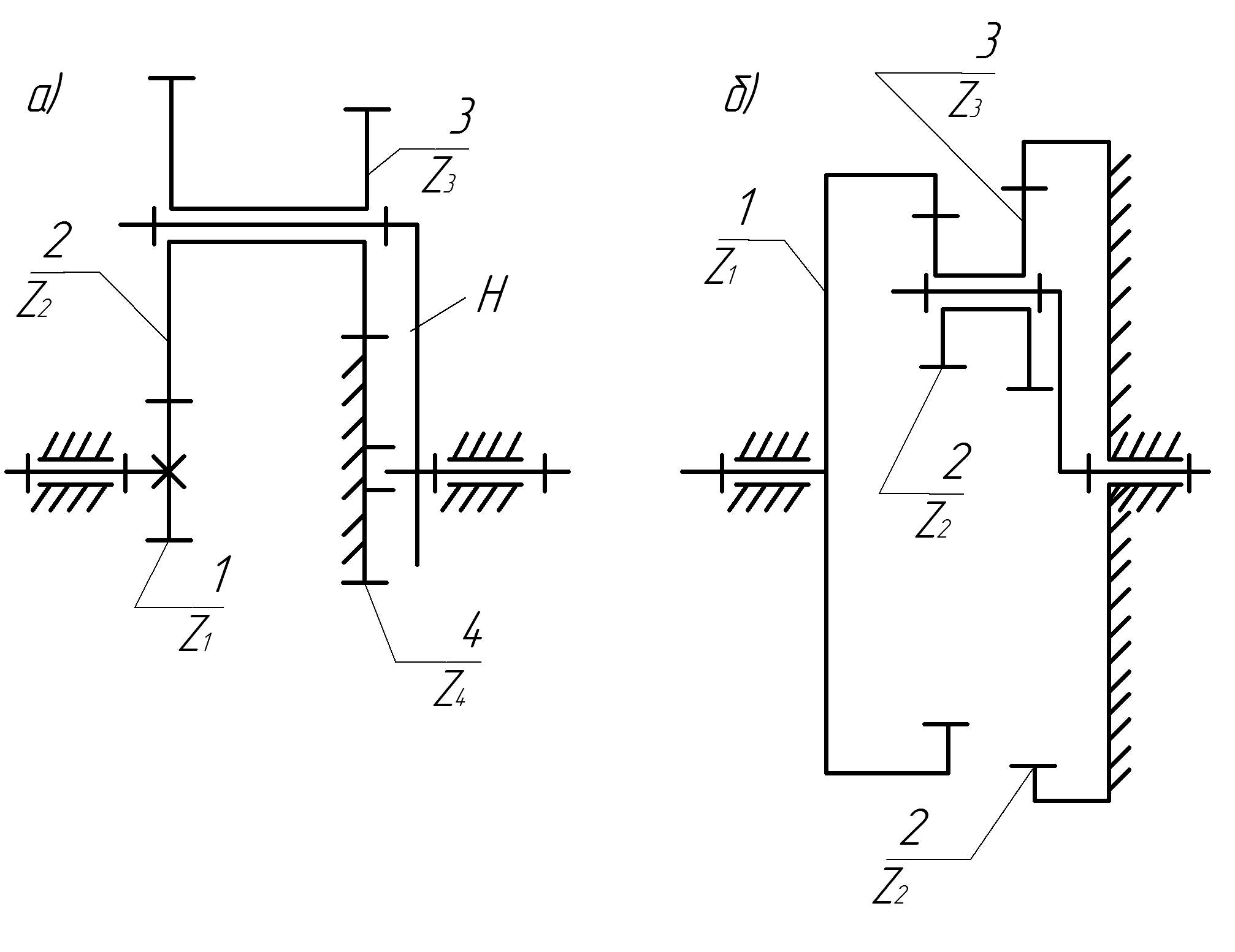
Данные механизмы используются как понижающие передачи (редукторы) с ведущим звеном – водилом Несмотря на большие кинематические возможности, механизмы этой группы целесообразно использовать в случаях, когда полезные нагрузки невелики, так как их КПД небольшой.

2. Схемы механизмов второй группы приведены на рис.14.3. Они составляются обязательно из колёс разнотипного зацепления с двойным (схема ) или одинарным (схема ) сателлитами.

) )

Рис. 14.3.

Механизмы второй группы широко применяются в силовых передачах средней и большой мощности, так как имеют высокий КПД. Они выполняются как многосателлитные редукторы, что позволяет значительно снизить их габариты и массу по сравнению с другими видами зубчатых передач одинакового передаточного отношения.

Для получения больших значений передаточных отношений механизмы второй группы применяются в комбинации с простыми зубчатыми передачами, а также в виде многоступенчатых механизмов (рис. 14.4).

Определение числа сателлитов планетарного и дифференциального механизмов.

Планетарные и дифференциальные механизмы выполняются многосателлитными. В существующих конструкциях число сателлитов находится в пределах К=2…12,но чаще всего составляет К=3…6. Наличие нескольких сателлитов позволяет значительно снизить габариты и массу механизма, улучшить его динамику, уравновешивая вращающиеся массы и разгружая опоры центральных колёс и водила.

Целесообразно определить максимально возможное число сателлитов из условия их соседства, т.е. совместного размещения по общей окружности в одной плоскости без задевания друг друга зубьями.

В однорядном механизме (рис.14.7) для выполненеия данного условия находим

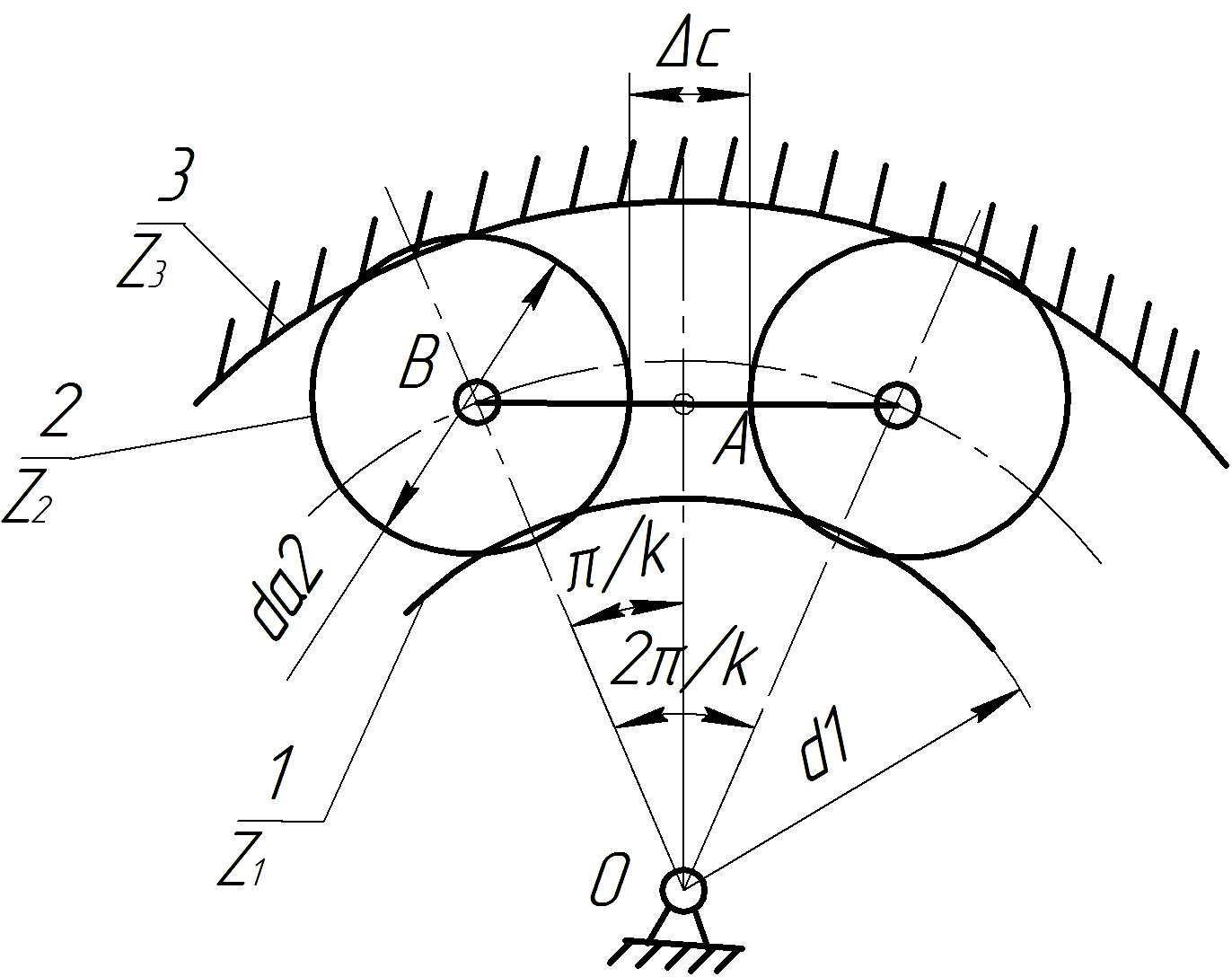
Рис.14.7.

• зазор ;

• размер ; (14.2)

• для внешнего зацепления колес 1, 2 из

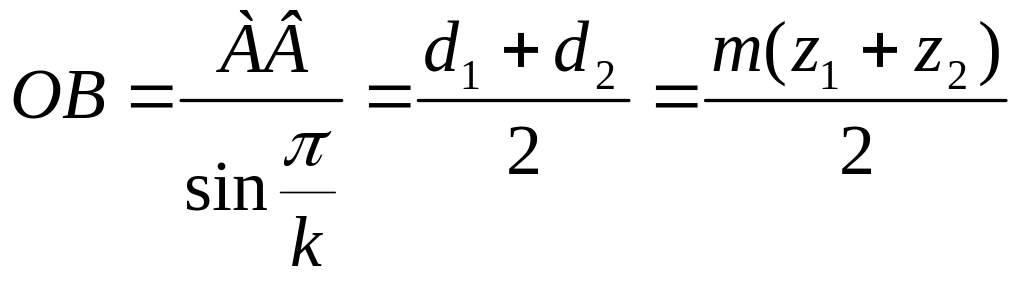; (14.3)

• диаметр вершин зубьев колеса 2

; (14.4)

Подставив выражения (14.3) и (14.4) в уравнение (14.2),получим

. (14.5)

Аналогично для внутреннего зацепления колес 2, 3 найдем

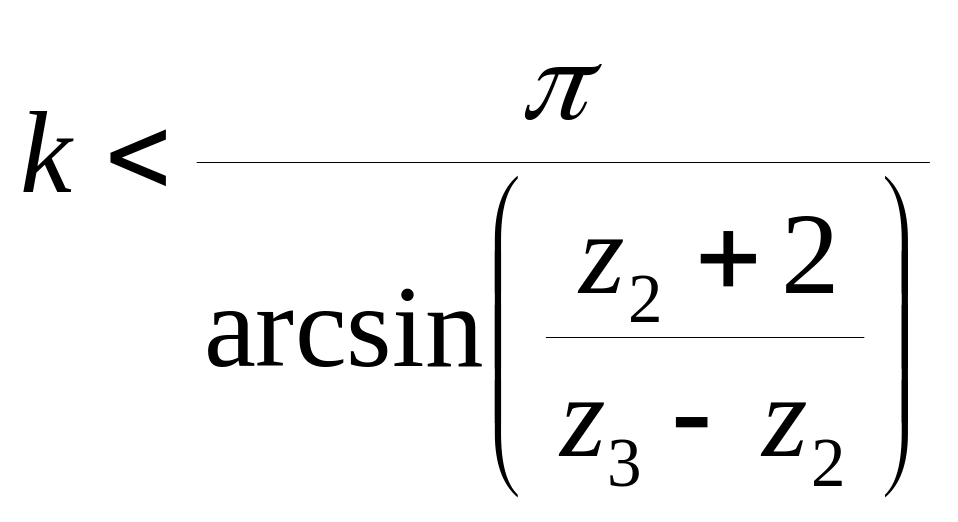. (14.6)

Определение чисел зубьев колес планетарного и дифференциального механизмов.

Важным этапом проектирования механизмов является определение чисел зубьев колес на основе выполнения ряда условий.

1. Обеспечение заданного передаточного отношения с допустимым отклонением ±2% для планетарного механизма.

2. Обеспечение соосности входного и выходного валов , при которой центральные зубчатые колеса и водило должны иметь общую геометрическую ось вращения.

3. Ограничение по числу сателлитов согласно уравнениям (14.5) и (14.6).

4. Обеспечение сборки (собираемости) механизма , когда зубья всех К сателлитов точно войдут во впадины между зубьями центральных колес при равных углах между сателлитами .

5. Исключение заклинивания зацеплений и подреза зубьев колес.

Так, для однорядного планетарного механизма, (рис.14.3, б) составленного из эвольвентных прямозубых нулевых колес , указанные условия дают уравнения :

—уравнение передаточного отношения

, откуда находим ;

—условие соосности (рис.14.7) , откуда находим , ;

—условие сборки - целое число;

—условие соседства (14.5) для нулевых колес (сателлитов) 2

.

Из полученных уравнений составим соотношение:

Z₁:Z₂:Z₃:

Оно позволяет подобрать числа зубьев колес, выполнив при этом условия, исключающие заклинивание зацеплений: ; ;

Принятое число сателлитов следует проверить по условию их соседства (14.5) или (14.6).