
- •3.Структурный анализ механизмов. Звенья механизма, их виды. (Билет №2) Кинематические пары и их классификация. Кинематическая цепь.
- •1) По виду места контакта (места связи) поверхностей звеньев:
- •4.Основные виды механизмов, их схемы и принцип действия.
- •5.Структурный синтез механизмов. Обобщённые координаты механизма и метод его определения. Методы структурного синтеза.
- •6.Кинематический анализ механизмов. Задачи и методы анализа плоских рычажных механизмов.
- •7.Графический метод кинематического анализа плоских механизмов. Планы скоростей и ускорений звеньев.
- •8.Кинематический анализ плоских механизмов в вкп (зубчатых).
- •9.Силовой расчёт механизмов. Задачи и методы силового расчёта. Реакции кп. Аналитический метод силового расчёта механизмов.
- •10.Динамическое исследование механизмов. Задачи и методы. Силы, действующие на звенья. Уравнение движения механизма в форме кинетической энергии.
- •11.Динамическое исследование механизмов. Приведение сил и масс в модели механизма.
- •12.Режимы движения механизмов. Дифференциальное уравнение движения механизмов.
- •13.Неравномерность движения механизмов. Коэффициент неравномерности. Расчёт параметров маховика.
- •14.Уравновешивание механизмов. Условия уравновешивания.
- •15.Уравновешивание механизмов. Статическое уравновешивание плоских механизмов.
- •20.Синтез плоских рычажных механизмов с нкп. Условие существования кривошипа. Синтез плоских механизмов по средней скорости выходного звена.
- •22.Уравновешивание вращающихся звеньев механизмов (роторов). Статическая и динамическая балансировка роторов.
- •23.Основная теорема зубчатого зацепления.
- •24.Эвольвентные профили зубьев. Параметры эвольвенты окружности.
- •25.Эвольвентное зацепление зубчатых колёс. Основные элементы и размеры зубьев колеса. (билет №42)
- •26.Способы изготовления зубчатых колёс. Изготовление эвольвентных колёс способом огибания. Ипк. (Билет 44) Подрезание и заострение зубьев.
- •27.Косозубая эвольвентная зубчатая передача. Основные параметры.
- •28.Коническая пространственная зубчатая передача.
- •29.Геометрические параметры эвольвентной зубчатой передачи и колёс. Выбор коэффициентов смещения (Билет 43-42)
- •30.Качественные показатели зубчатой передачи.
- •31.Червячная передача.
- •32.Угол давления кулачкового механизма и его выбор.
- •33.Синтез кулачковых механизмов. Этапы синтеза. Выбор закона движения толкателя.
- •34.Определение начального радиуса r0 кулачка для механизмов с поступательным движением толкателя.
- •35.Синтез кулачковых механизмов. (Билет 33) Выбор радиуса ролика толкателя. Определение жесткости замыкающей пружины.
- •36.Эвольвентные профили зубьев колёс. Эвольвента и её уравнение (Билет №37).
- •37.Основные элементы и размеры зубьев колёс. ( Билет 42) Эвольвента и её уравнение.
- •38.Определение начального радиуса r0 кулачка для механизмов с коромысловым толкателем.
- •39.Основные схемы кулачковых механизмов. (Билет 40) Методы замыкания кулачковых механизмов. Схемы замыкания.
- •40.Кулачковые механизмы. Виды кулачковых механизмов и их особенности.
- •41.Планетарные зубчатые механизмы. Выбор схемы, числа сателлитов и чисел зубьев колёс.
- •42.Геометрические параметры эвольвентной зубчатой передачи и зубчатых колёс.
- •43.Выбор коэффициентов смещения зубчатых колес.
- •44.Изготовление эвольвентных зубчатых колёс способом огибания. Ипк.
32.Угол давления кулачкового механизма и его выбор.
Угол
давления является второй важной
характеристикой механизма, определяющей
его работоспособность, КПД
и габаритные размеры. Это угол
![]() между нормалью n-n
к профилю кулачка 1,
в точке его касания с толкателем 2,
и вектором скорости
между нормалью n-n
к профилю кулачка 1,
в точке его касания с толкателем 2,
и вектором скорости
![]() перемещения толкателя (рис.15.5).
Дополнительный к углу давления угол
перемещения толкателя (рис.15.5).
Дополнительный к углу давления угол
![]() называют углом
передачи движения.
называют углом
передачи движения.
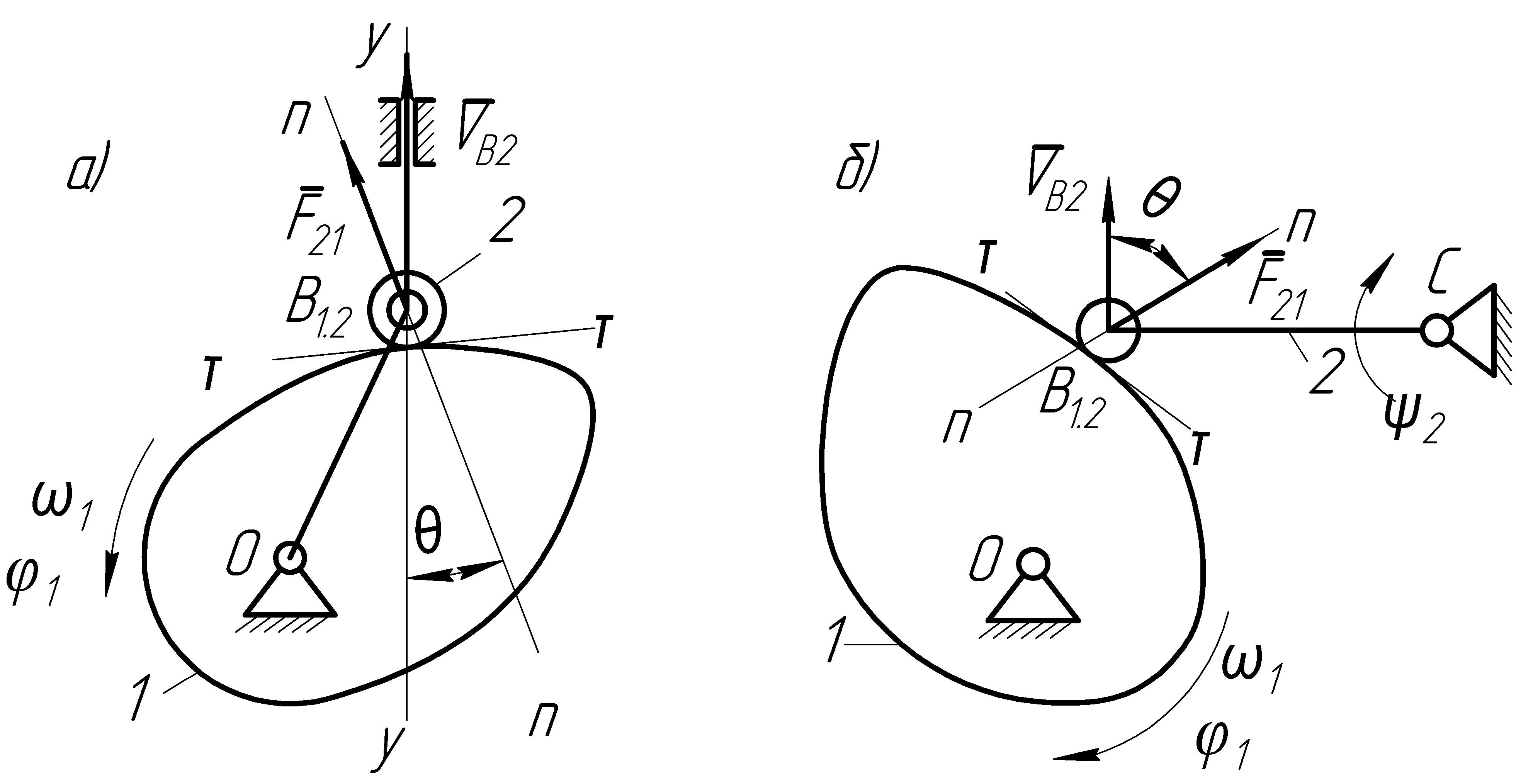
Рис.15.5.
Векторная схема определения угла
давления
![]() :
:
![]() – вектор
силы давления кулачка 1
на толкатель
2;
– вектор
силы давления кулачка 1
на толкатель
2;
![]() – касательная
к профилю кулачка
– касательная
к профилю кулачка
Для
определения угла
строим план скоростей механизма
(рис.15.6, а)
в масштабе
![]() по векторному уравнению (для схемы на
рис.15.5, а)):
по векторному уравнению (для схемы на
рис.15.5, а)):
![]() где
где
![]() – переносная скорость ролика
– переносная скорость ролика
![]() .
.
![]()
![]()
![]()
![]() – относительная
скорость качения ролика по кулачку.
– относительная
скорость качения ролика по кулачку.
Повернём
план скоростей в направлении
![]() на 90° и разместим его в масштабе
на 90° и разместим его в масштабе
![]() на плане
механизма
(рис.15.6
на плане
механизма
(рис.15.6
![]() ).
).
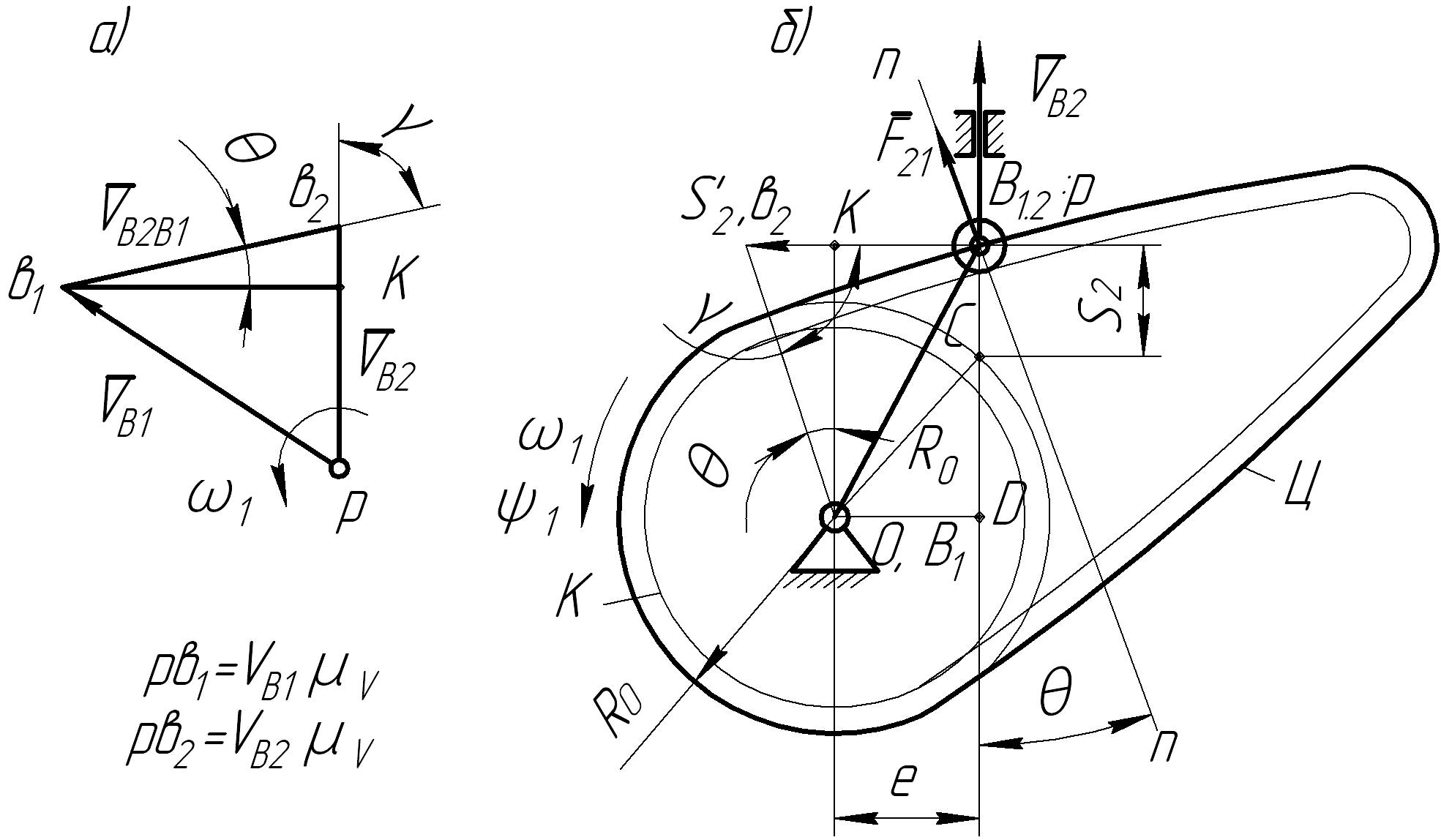
Рис.15.6.
Используя
исходную зависимость для перемещения
толкателя
![]() ,
и параметры плана скоростей, находим:
,
и параметры плана скоростей, находим:
1.
![]() , где
, где
![]() - аналог скорости толкателя 2;
- аналог скорости толкателя 2;
2.
![]() .
(15.1)
.
(15.1)
3.
![]() .
.
Но
из рис.15.6, б
следует, что
![]() .
.
Поэтому
находим
![]() .
(15.2)
.
(15.2)
Подставив
соотношение (15.2) в (15.1) , получим
![]() -
аналог скорости толкателя в масштабе
-
аналог скорости толкателя в масштабе
![]() плана механизма. Из треугольника
плана механизма. Из треугольника
![]() находим основную расчетную зависимость
механизма:
находим основную расчетную зависимость
механизма:
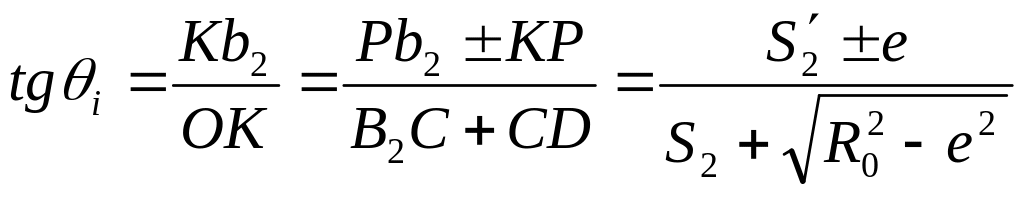 ,
(15.3)
,
(15.3)
где е – смещение оси толкателя относительно оси вращения кулачка.
Аналогичный план скоростей, совмещенный с планом механизма с коромысловым толкателем, представлен на рис.15.7.
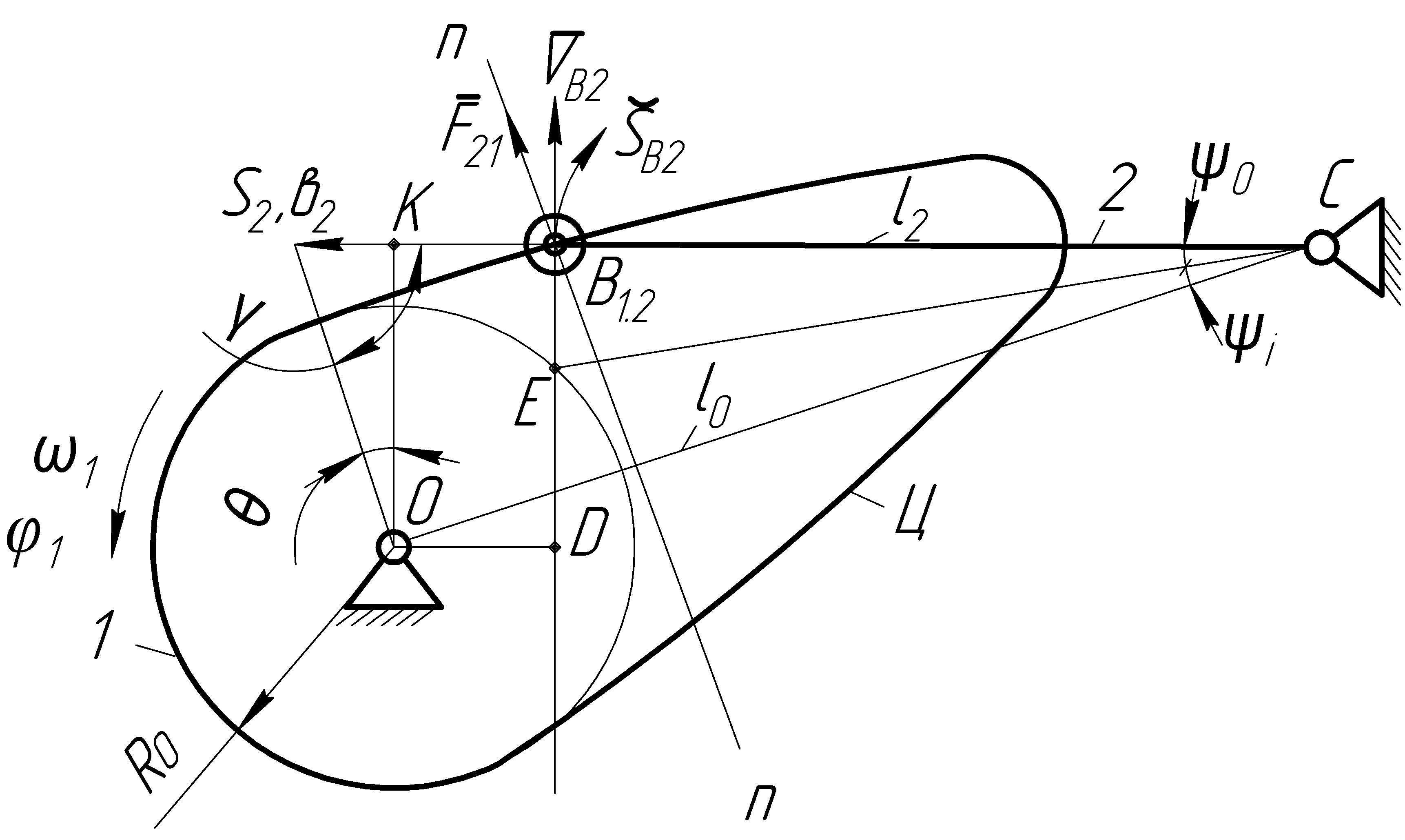
Рис.15.7.
Из него находим
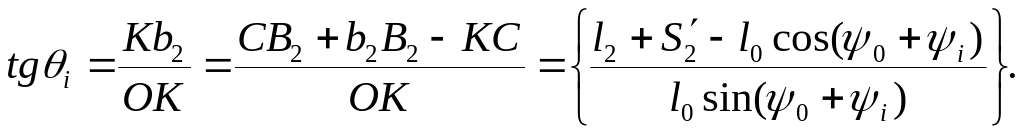 (15.4)
(15.4)
Допустимое
значение угла давления
![]() выбирают так, чтобы обеспечить минимальные
габариты механизма
выбирают так, чтобы обеспечить минимальные
габариты механизма
![]() и достаточно высокий КПД
и достаточно высокий КПД
![]() .
Для этого используют экспериментально-теоретические
зависимости для КПД
(рис.15.8).
.
Для этого используют экспериментально-теоретические
зависимости для КПД
(рис.15.8).
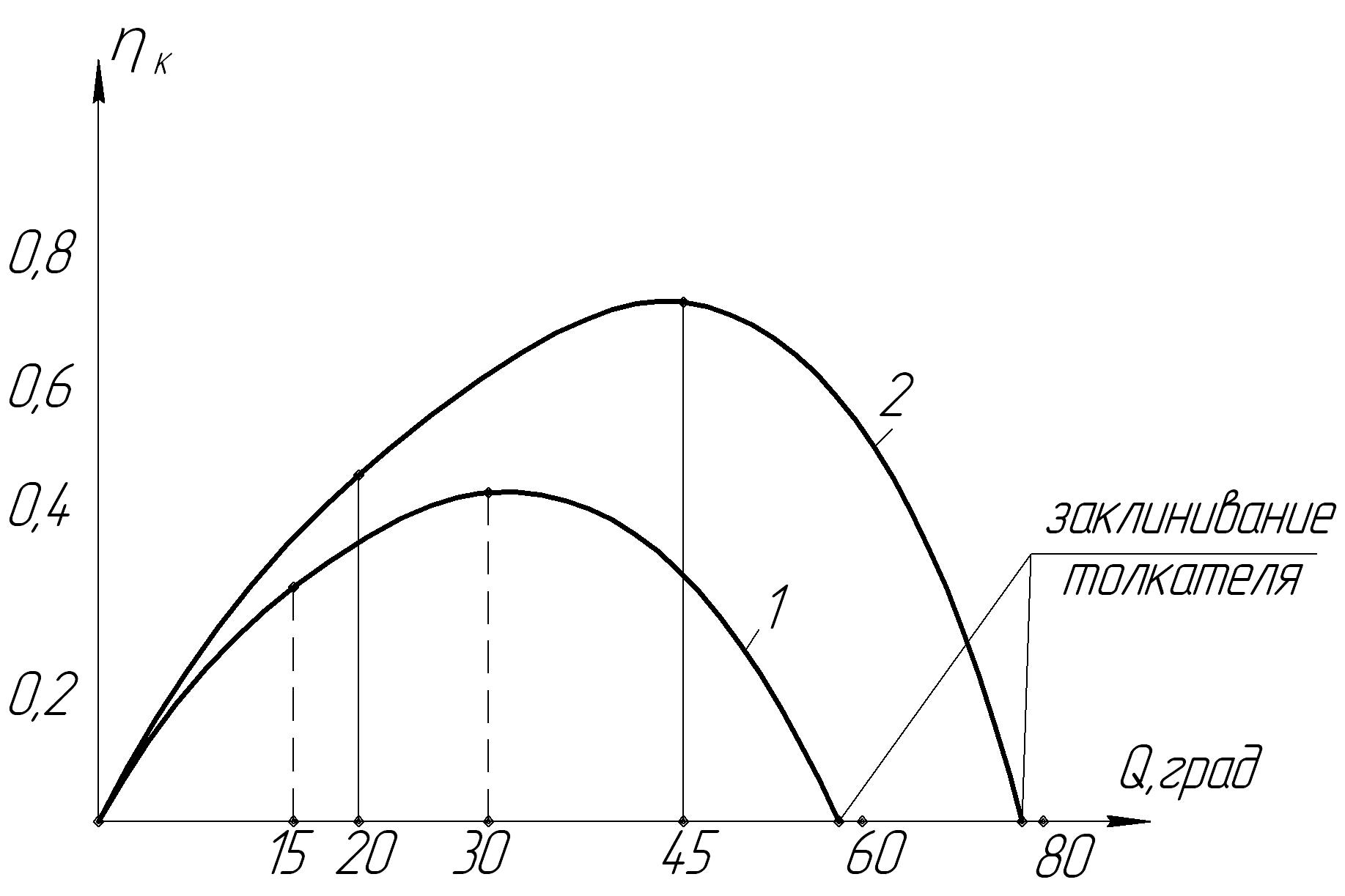
Рис. 15.8. Зависимость для КПД механизмов:
1 – с поступательно движущимся толкателем;
2 – с коромысловым толкателем.
Для ориентировочных расчетов принимают:
![]() -
для поступательно движущегося толкателя;
-
для поступательно движущегося толкателя;
![]() -
для коромыслового толкателя.
-
для коромыслового толкателя.
Для
уменьшения габаритов механизма принимают
![]() с некоторым уменьшением КПД,
но исключением заклинивания толкателя
при
с некоторым уменьшением КПД,
но исключением заклинивания толкателя
при
![]() и
и
![]() соответственно.
соответственно.
Принятым
значениям угла давления соответствуют
минимальные значения угла передачи
движения:
![]() ;
;
![]() .
.
33.Синтез кулачковых механизмов. Этапы синтеза. Выбор закона движения толкателя.
При синтезе кулачкового механизма, как и при синтезе любого механизма, решается ряд задач из которых в курсе ТММ рассматриваются две:
выбор структурной схемы и определение основных размеров звеньев механизма (включая профиль кулачка и т.п. Если оси параллельны, то выбирается плоская схема механизма. При пересекающихся или перекрещивающихся осях необходимо использовать пространственную схему. В кинематических механизмах нагрузки малы, поэтому можно использовать толкатели с заостренным наконечником. В силовых механизмах для повышения долговечности и уменьшения износа в схему механизма вводят ролик или увеличивают приведенный радиус кривизны контактирующих поверхностей высшей пары.
Синтез механизма включает этапы:
1. Синтез структурной схемы механизма.
2. Выбор закона перемещения толкателя.
3. Определение основных размеров механизма.
4. Определение координат профиля кулачка.
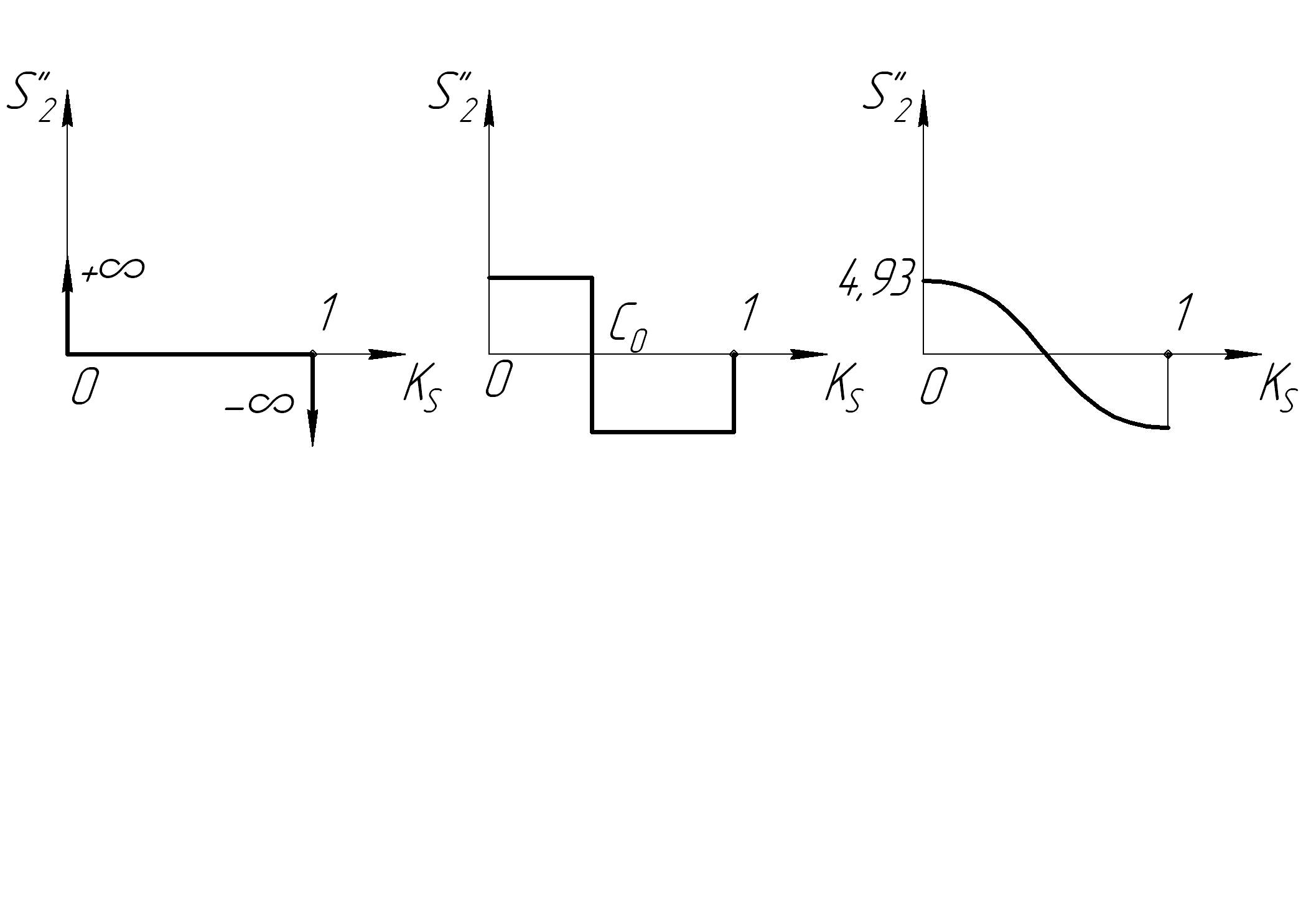
В технике наибольшее применение получили относительно простые законы перемещения толкателя (рис.15.4):
![]() )
линейный
)
параболический
)
линейный
)
параболический ![]() )
косинусоидальный
)
косинусоидальный
![]()
![]()
![]()
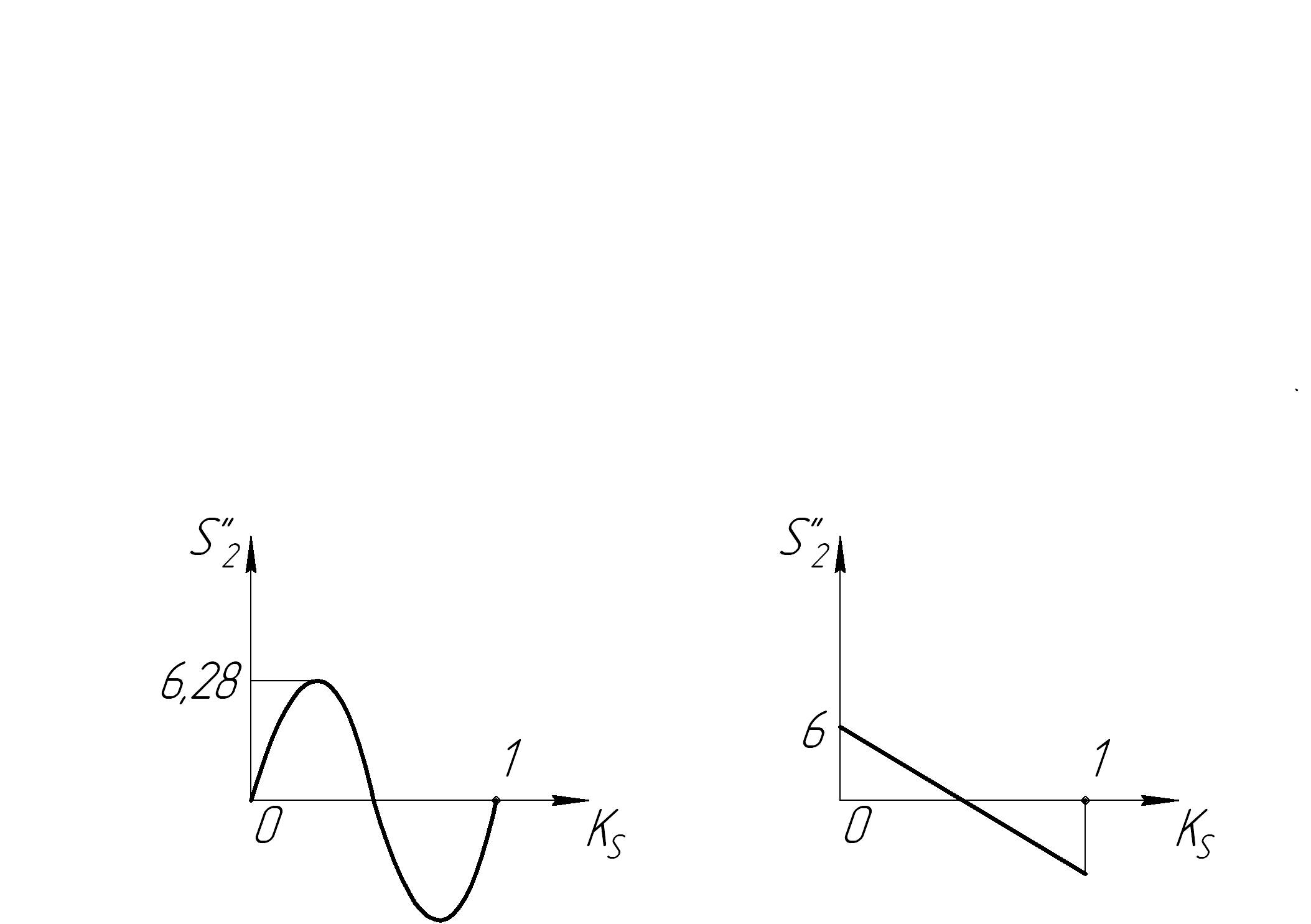
![]() )
синусоидальный
)
синусоидальный ![]() )
равноубывающий
)
равноубывающий
симметричный
![]()
![]()
Рис.15.4.
На
графиках и в формулах:![]() – относительный угол поворота кулачка
на фазе удаления;
– относительный угол поворота кулачка
на фазе удаления;
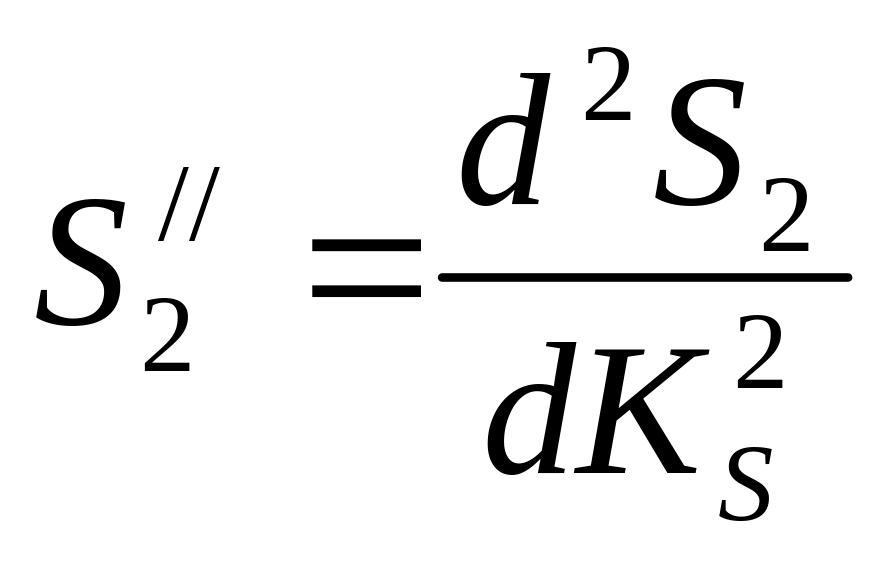 - аналог ускорения толкателя.
- аналог ускорения толкателя.
1.
Для линейного закона перемещения
толкателя в точках
![]() и
и
![]() ускорения
ускорения
![]() и
и
![]() .
Здесь модули сил инерции толкателя
теоретически составляют
.
Здесь модули сил инерции толкателя
теоретически составляют
![]() ,
что вызывает «жёсткие удары» кулачка
по толкателю. Эти звенья подвергаются
деформации и интенсивному изнашиванию.
Линейный закон используют в тихоходных
механизмах при требуемой постоянной
скорости
движения толкателя. Так, в металлорежущих
автоматах он реализуется профилированием
рабочего участка кулачка по архимедовой
спирали (привод суппорта станка и т.п.).
,
что вызывает «жёсткие удары» кулачка
по толкателю. Эти звенья подвергаются
деформации и интенсивному изнашиванию.
Линейный закон используют в тихоходных
механизмах при требуемой постоянной
скорости
движения толкателя. Так, в металлорежущих
автоматах он реализуется профилированием
рабочего участка кулачка по архимедовой
спирали (привод суппорта станка и т.п.).
2.
В точках разрыва кривой ускорения
![]() ,
характерного для законов
,
характерного для законов
![]() ,
,
![]() ,
,
![]() ,
силы инерции толкателя изменяются на
конечную величину. В этих точках имеют
место «мягкие удары». Работа механизма
сопровождается вибрациями, шумом и
повышенным изнашиванием звеньев. Данные
законы применяют при умеренных скоростях
движения толкателя.
,
силы инерции толкателя изменяются на
конечную величину. В этих точках имеют
место «мягкие удары». Работа механизма
сопровождается вибрациями, шумом и
повышенным изнашиванием звеньев. Данные
законы применяют при умеренных скоростях
движения толкателя.
3.
Для законов с плавным, безразрывным
изменением ускорения толкателя
![]() (закон
(закон
![]() на рис.15.4) удары теоретически отсутствуют.
Эти законы используют чаще других.
на рис.15.4) удары теоретически отсутствуют.
Эти законы используют чаще других.
Основные положения по выбору закона перемещения толкателя:
— в
быстроходных механизмах при скоростях
вращения кулачка
![]() необходимо использовать “безударные”
законы с плавным и безразрывным изменением
аналога ускорения толкателя:
– синусоидальный, полиномиальные
(степенные). Они обеспечивают хорошие
динамические показатели механизма;
необходимо использовать “безударные”
законы с плавным и безразрывным изменением
аналога ускорения толкателя:
– синусоидальный, полиномиальные
(степенные). Они обеспечивают хорошие
динамические показатели механизма;
— в механизмах с меньшими частотами вращения кулачка предпочтительно использовать законы с “мягкими” ударами – полиномиальные, равноубывающий косинусоидальный, параболический. Желательны и безударные законы;
— законы,
вызывающие “жесткие” удары, допустимы
только для весьма тихоходных и лёгких
конструкций механизмов: линейный; с
профилем кулачка по архимедовой спирали
![]() .
.
