7 .7. Тензор інерції

Розглянемо обертальний рух тіла відносно закріпленої точки О, котра співпадає з початком інерціальної системи відліку (рис 7.12).

Проведемо через точку О миттєву вісь ОА. Нехай – миттєва кутова швидкість тіла відносно ціеї осі. Момент імпульсу частинки цього тіла відносно точки О:

Рис.7.12.

Момент імпульсу всього тіла

Всі частинки тіла мають одну й ту саму кутову швидкість . Тому рівняння моменту імпульсу можна записати в проекціях на осі координат, наприклад:

Оскільки то

Подібні рівняння можна записати для та . Останнє рівняння має три коефіцієнти:

.

Кожен із цих коефіцієнтів залежить від миттєвої орієнтації тіла від-носно осей координат . Їх називають інерціальними коефіцієнтами або моментами інерції:

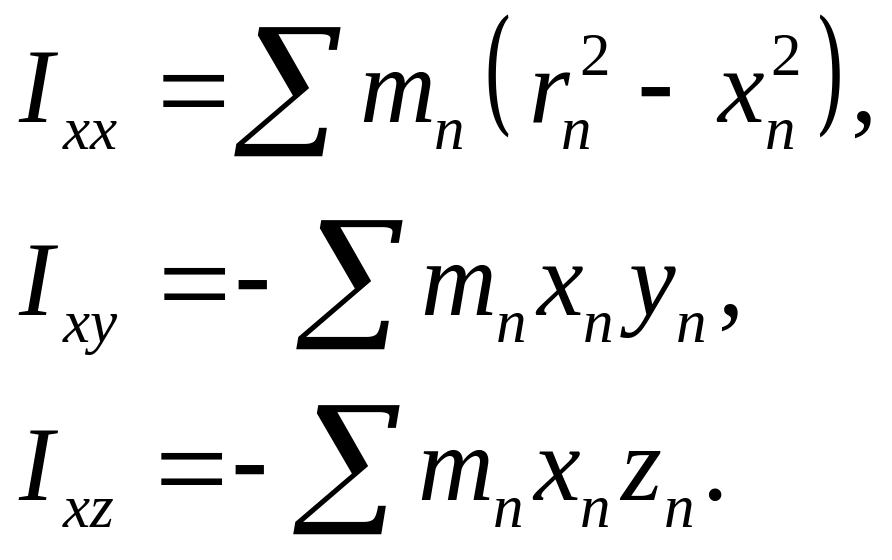(7.35)

Аналогічно можна записати коефіцієнти для проекцій та . Врахо-вуючи всі коефіцієнти та рівняння, отримуємо систему рівнянь для всіх компонентів моменту імпульсу:

(7.36)

Сукупність дев’яти величин

(7.37)

називають тензором інерції тіла відносно точки О, а самі ці величини – компонентами цього тензора, або компонентами матриці (див. [4] та [5]).Сукупність рівнянь (7.36) вказує на те, що у випадках тіл довільної форми з довільним розподілом маси момент імпульсу не є простим добутком скаляра на вектор кутової швидкості. Тому взагалі напрямок вектора не співпадає з напрямком вектора .

Величини називають діагональними компонентами тензора, а всі інші – недіагональними. Вони симетричні: . Діагональні компоненти, наприклад є сумою добутків кожної маси на квадрат її відстані від осі обертання, тому їх називають моментами інерції відносно осі.

Якщо – густина тіла в точці, радіус-вектор якої є , то кожен мо-мент інерції можна записати у вигляді інтегралів, наприклад:

.

Очевидно, що сума діагональних компонентів

(7.38)

На підставі рівняння (7.38) обчислимо головний момент інерції однорідної кулі радіуса , мас якої :

що співпадає з результатами (7.6.7).

7.8. Кінетична енергія обертального руху тіла

Умовно розіб'ємо тіло на N елементарних мас Δm_i (рис.7.13). Кінетична енергія однієї такої маси дорівнює:

.

Кінетична енергія всього тіла, зумовлена тільки обертанням тіла, дорівнює сумі кінетичних енер-гій усіх елементарних мас: (7.39)

Рівняння (7.39) справедливе при обертанні тіла відносно довільно обраної осі обертання. Знайде-

Рис.7.13 мо роботу, яку необхідно виконати над тілом, щоб повернути його на деякий кут φ. З огляду на співвідношення між кі-нетичною енергією тіла та роботою на підставі рівняння (7.39), знаходимо:

Оскільки вектори й паралельні, а момент інерції не залежить від швидкості , то елементарну роботу можна виразити в такий спосіб:

Скориставшись основним рівнянням динаміки обертального руху у вигляді: , знаходимо:

Тоді:

Для повороту тіла на кут φ необхідно виконати роботу:

. (7.40)

Це і є робота сили, що обертає тіло.

Обертання тіла навколо закріпленої точки в будь-який момент часу можна розглядати як його обертання навколо миттєвої осі, що проходить через закріплену точку. Тоді кінетична енергія обертального руху тіла й робота обертання цього тіла можуть бути описані тими ж рівняннями (7.39) і (7.40) з тією лише різницею, що момент інерції й момент сили потрібно розглядати відносно миттєвої осі обертання, у зв'язку з чим вони не будуть залишатися незмінними у часі, оскільки сама миттєва вісь змінює своє положення в просторі.