7.2. Момент сили відносно осі
Нехай
на тіло із закріпленою віссю z
діє довільно спрямована сила
(рис.
7.4). Тоді тіло може обертатися тільки
навколо осі z
.
Знайдемо момент сили відносно точки О,
яка лежить на осі обертання, а потім
виділимо складову моменту
,
паралельну осі z:
(7.10)
Радіус-вектор
можна представити у вигляді суми:
Тоді
складова
буде дорівнює
Векторний
добуток
дає вектор, перпендикулярний
,
тобто він перпендикулярний осі z,
і проекція цього вектора на вісь z
дорівнює
нулю:
,
а
Розкладемо
силу
на три складові:
Тоді
одержимо: 
У цьому
рівнянні перша складова дорівнює нулю,
оскільки вектори
і
паралельні,
друга
складова дорівнює нулю, тому що вектор
перпендикулярний осі z. Таким чином, складова моменту і її проекція дорівнюють:
(7.11)
Рис.7.4
З усіх складових сили тільки одна її складова здатна обертати тіло навколо осі z. Тому одні автори (див.[2], [3]) саму складову моменту сили , інші (див. [1], [4], [6], [7]) – її проекцію на вісь обертання називають моментом сили відносно осі обертання z.
Якщо на тіло діє кілька сил, то повний момент цих сил відносно осі обертання дорівнює сумі моментів усіх сил:
(7.12)
7.3. Момент імпульсу матеріальної точки
Нехай
деяка матеріальна точка m
рухається зі швидкістю
,
як пока-зано на рис. 7.5. Момент імпульсу
цієї матеріальної точки відносно дея-кої
точки 0 визначається аналогічно моменту
сили:
(7.13)
Модуль моменту імпульсу дорівнює:
(7.14)
Складова моменту імпульсу, паралельна осі z, навколо якої може обертатися деяка мате-ріальна точка або тіло, виражається рівнянням:
(7.15)
Розклавши
вектор
на три складові
,
а вектор
на складові
та
(рис. 7.6) і підставивши ці значення в
рівняння (7.15), знайдемо:
(7.16)
Продиференціюємо
рівняння
за
часом.
Рис.7.5 Рис.7.6
Перший
доданок дорівнює нулю, оскільки
,
а доданок
дорівнює моменту сили. Таким чином,
швидкість зміни моменту імпульсу тіла
дорівнює моменту сил, що діють на тіло:
(7.17) Оскільки у відповідності з правилом
диференціювання векторів для будь-якого
вектора
справедливе співвідношення
то, про-диференціювавши за часом рівняння
,
одержимо:
(7.18)
Напрямок моменту імпульсу, як і моменту сили, визначається пра-вилом векторного добутку.
7.4. Закон збереження моменту імпульсу
Розглянемо
рівняння (7.17) для системи матеріальних
точок, що взає-модіють між собою. У
загальному випадку для кожної
-ї
матеріальної точ-ки це рівняння буде
мати вигляд:
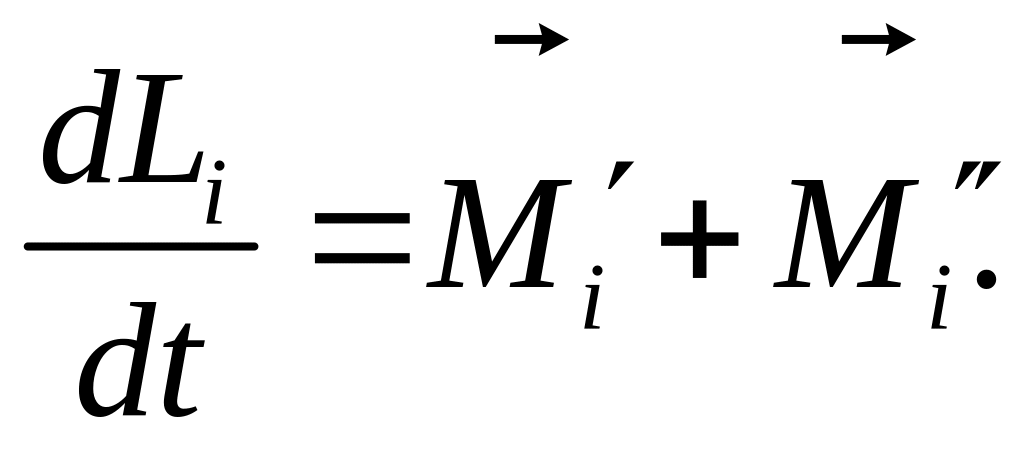(7.19)
де
-
сумарний
момент внутрішніх сил, що діють на цю
точку, а
-
сумарний момент зовнішніх сил, що діють
на цю саму точку. Всій системі матеріальних
точок відповідає N
таких рівнянь.
Склавши ці рівняння, одержимо:
(7.20)
Величину:
(7.21)
називають моментом імпульсу системи матеріальних точок.
Відповідно до третього закону Ньютона і визначення поняття момен-ту сили відносно точки сумарний момент внутрішніх сил відносно будь-якої точки (а значить і відносно осі) дорівнює нулю. Отже, рівняння (7.20) набирає вигляду:
(7.22)
Відповідно
до визначення поняття замкненої системи
тіл, на неї зовнішні сили не діють, а це
означає, що для замкненої системи тіл
і
рівняння (7.22) зводиться до такого:
,
(7.23)
звідки випливає, що момент імпульсу замкненої системи матеріальних то-чок залишається незмінним. Це твердження становить зміст закону збере-ження моменту імпульсу.
Спроектувавши
всі величини, що входять у рівняння
(7.22), на деякий напрямок z
і
домноживши
на орт цього напрямку, одержимо:
(7.24)
Із цього рівняння випливає таке: якщо сумарний момент сил відносно осі дорівнює нулю, то момент імпульсу відносно цієї осі залишається не-змінним.