4.6. Закон збереження імпульсу замкненої системи тіл

Розглянемо систему, що складається з n матеріальних точок (тіл). Сили , з якими тіла системи взаємодіють між собою, назвемо внутріш-німи, а сили , з якими тіла системи взаємодіють із зовнішніми тілами – зовнішніми. Систему тіл, що взаємодіють між собою й не взаємодіють з зовнішніми тілами, називають замкненою.

Імпульс системи тіл дорівнює векторній сумі імпульсів всіх тіл, що утворюють систему:

(4.24)

Знайдемо швидкість центра інерції системи:

Таким чином, імпульс системи тіл дорівнює:

(4.25)

Нехай система складається з трьох тіл, і на кожне тіло, крім внутріш-ніх сил , діють зовнішні сили (рис. 4.4). Для кожного з тіл запишемо другий закон Ньютона:

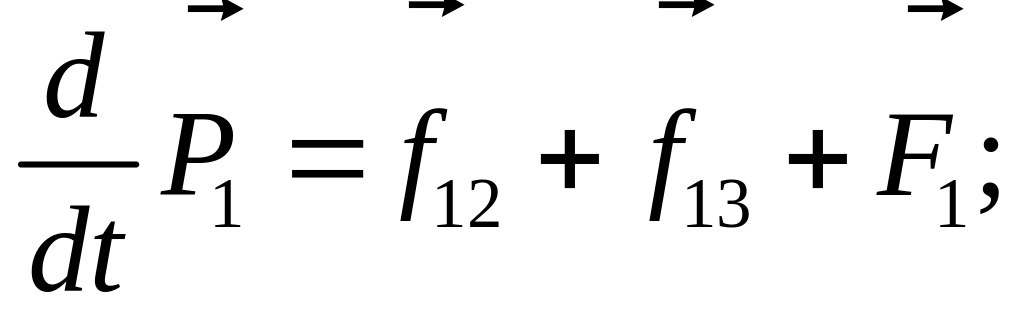
Додамо всі три рівняння:

(4.26)

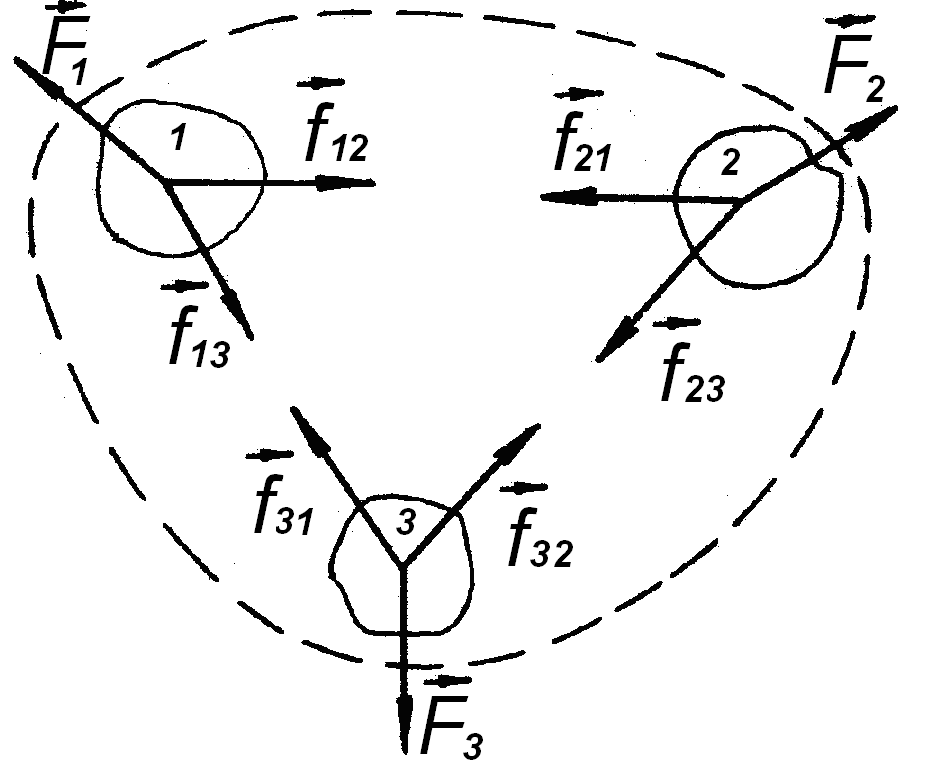
Рис. 4.4

Відповідно до третього закону Ньютона сума внутрішніх сил . Тоді, для довільної системи, що складається з n – ої кількості тіл, знахо-димо:

(4.27)

отже швидкість зміни імпульсу системи тіл дорівнює сумарній зовнішній силі, що діє на цю систему. Для замкненої системи за визначен-ням поняття замкненої системи. Тоді:

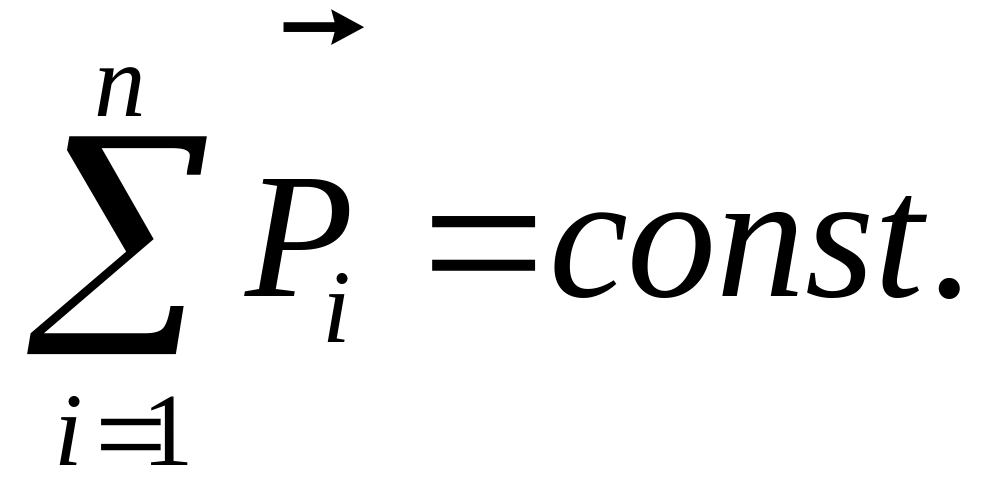(4.28)

Повний імпульс замкненої системи тіл зберігається. Це і є закон збереження імпульсу. Він є одним із фундаментальних законів природи і проявляється в цілому ряді явищ. Зокрема, він лежить в основі реактивного руху.

4.7. Реактивний рух

Р еактивний рух – це рух ракети під дією сили віддачі струменя газів, що витікає з сопла реактивного двигуна. Знайдемо швидкість раке-ти в залежності від зміни її маси. Нехай у момент часу швидкість ракети відносно Землі дорівнює , а її маса m. Імпульс ракети в цей момент Рис. 4.5 часу дорівнює . Нехай в цей момент часу з ракети починають виходити вихлопні гази з постійною швидкістю відносно ракети (рис. 4.5); відносно Землі швидкість газів буде дорівнювати . Після закінчення часу швидкість ракети стане рівною , а її маса , де – маса газів, що вийшли, швидкість яких відносно Землі буде . Імпульс системи в момент часу буде дорівнювати:

Згідно з законом збереження імпульсу знаходимо:

звідки одержимо: У початковий момент часу швидкість ракети дорівнювала нулю, а маса – початковій масі . Інтегруючи останню рівність із урахуванням початкових умов, прийнявши , знаходимо:

(4.29)

Знак "мінус" вказує на протилежний напрямок швидкостей і . Рівняння (4.29) називають формулою Ціолковського, тому що вперше вона була отримана саме Ціолковським. Швидкість ракети зростає тим швидше, чим швидше зменшується її маса. Тому ракети роблять багато-ступінчастими.