Лемма (Больцано-Вейерштрасса).

Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство:

Пусть дана ограниченная последовательность для .

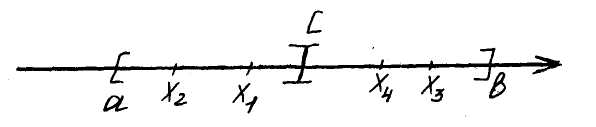
Некоторой точкой разобьем промежуток на две части. Хотя бы в одном из полученных промежутков будет находиться бесконечное число членов последовательности. Возьмем такой промежуток и разобьем еще раз пополам и т.д. Повторим эту процедуру и получим последовательность вложенных промежутков: - последовательность замкнутых, конечных, вложенных промежутков. Получим стягивающуюся последовательность, т.к. , следовательно, по лемме из §3.10. существует единственная точка, которая будет принадлежать всем промежуткам последовательности.

Теперь из промежутка возьмем какой-либо член последовательности, например, с наименьшим номером среди членов, лежащих в этом промежутке. Обозначим его

Из берем ;

Из берем , и т.д.

Получим последовательность , которая является подпоследовательностью исходной.

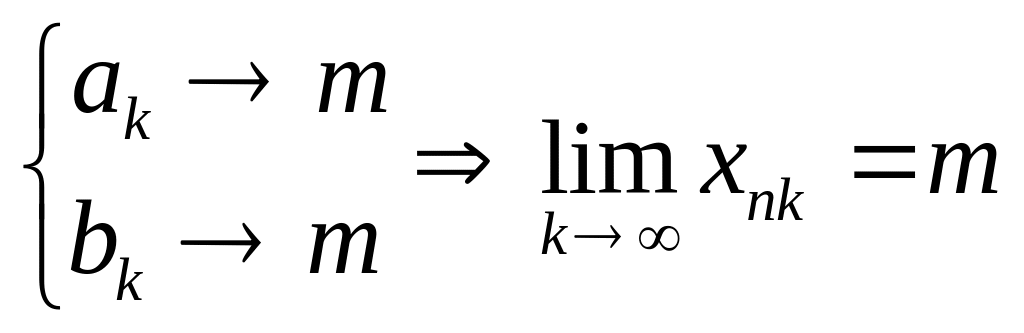(по принципу двух милиционеров)

§3.12. Критерий Больцано-Коши сходимости последовательности.

Определение Последовательность называется фундаментальной (сходимость в себе), если для , т.е. достаточно далекие члены последовательности отличаются друг от друга как угодно мало.

Теорема (критерий Больцано-Коши).

Для того, чтобы последовательность сходилась необходимо и достаточно, чтобы она была фундаментальной ( по определению предела ).

Замечание: критерий Больцано-Коши дает возможность определить, сходится последовательность или нет, не вычисляя самого предела, а лишь по поведению членов этой последовательности.

Теорема 2 (критерий Больцано-Коши: существования конечного предела функции).

Для того, чтобы функция при имела конечный предел необходимо и достаточно, чтобы для .

Лекция №7

§3.13. Некоторые эквивалентности и формулы полезные при вычислении пределов.

При вычислении пределов часто встречаются неопределенности следующего типа:

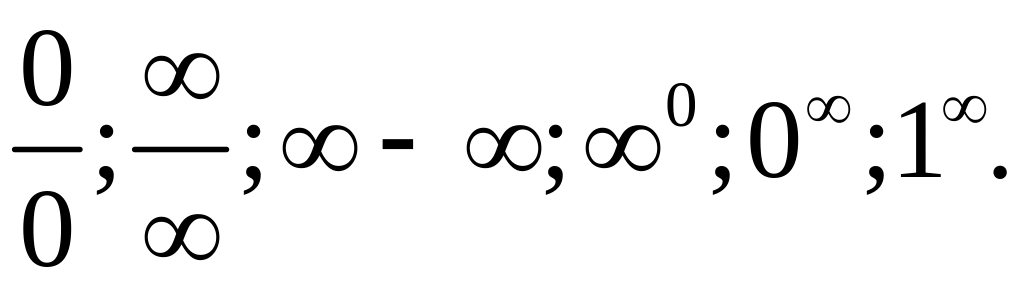
. При справедливы следующие эквивалентности (вытекают из первого замечательного предела ):

.

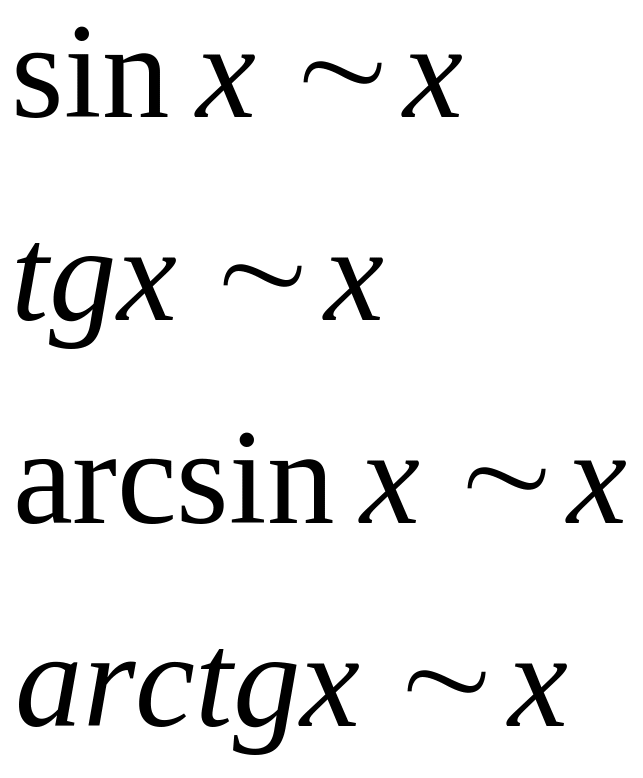
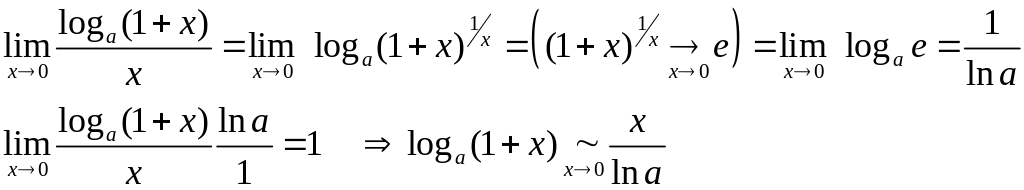
при

при

.

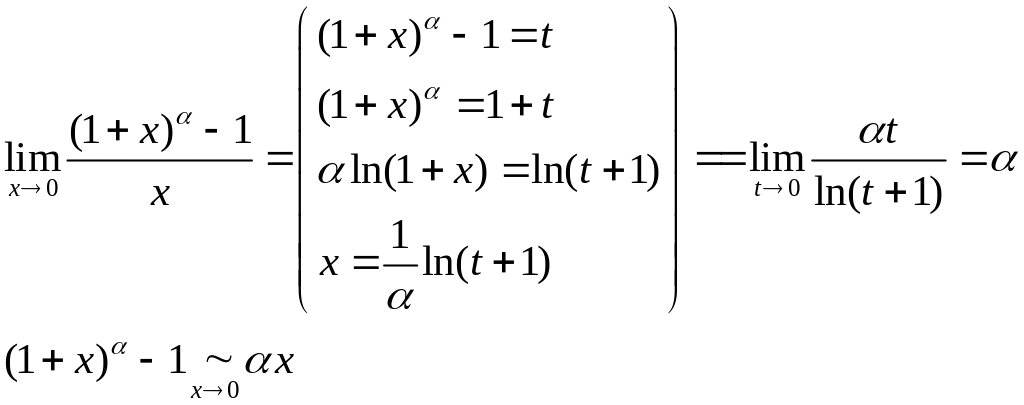
Предел степенно-показательной функции.

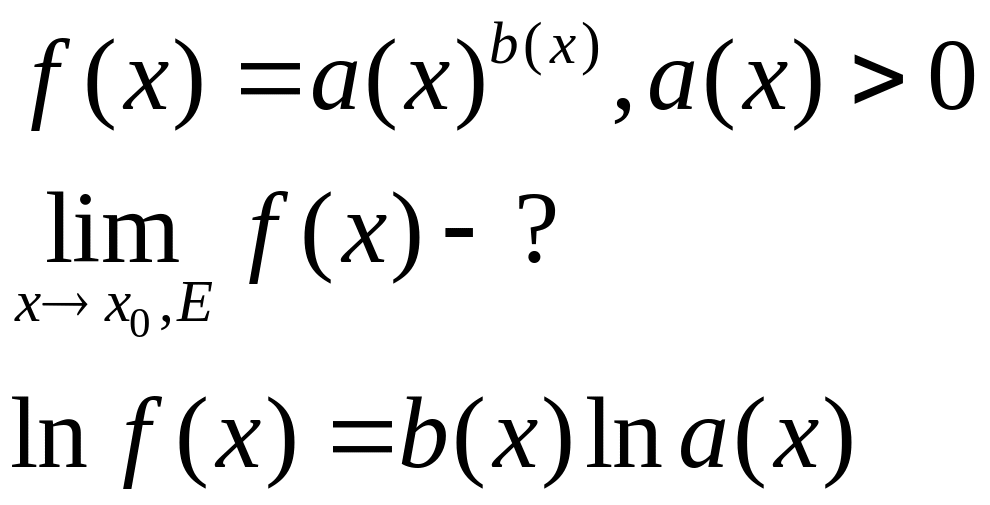
Пусть

Если предел существует, то можно найти и сам предел функции.

§4. Непрерывные функции.

§4.1. Понятие непрерывной функции.

Путь задана функция:

Определение 1. Функция называется непрерывной в точке относительно множества , если

Функция непрерывна в точке относительно множества , относительно множества -нет.

Определение 2(на языке окрестностей). Функция называется непрерывной в точке относительно множества , если для

Если функция непрерывна в каждой точке своей области определения , то говорят, что она непрерывна на всем или просто непрерывна.

§4.2. Свойства непрерывной функции.

Свойство 1.

Если:

1) непрерывна в точке относительно множества ;

2)

тогда является непрерывной в точке относительно .

Свойство 2. Для любой фиксированной окрестности точке ( ) непрерывность функции в точке относительно равносильно непрерывности в точке относительно .

Свойство 3. Если множество , тогда непрерывность функции в точке относительно множества равносильно непрерывности как относительно , так и относительно .

Замечание: Если в свойстве 3 является предельной только для одного из множеств( или ), то непрерывности функции относительно всего будет равносильно непрерывности относительно этой части.

Свойство 4(предельный переход под знаком непрерывной функции).

Если:

1) непрерывна в точке относительно множества ;

2) , причем область значения

тогда предел сложной функции или

Следствие (из свойства 4):