§6.7. Правило Лапиталя. Теорема (правило Лапиталя-Бернулли).

Пусть функции определены на могут быть бесконечными). Пусть выполнено следующее условие:

1) дифференцируемы на ;

2) на ;

3) ;

4)

тогда (1)

Замечание 1. Основные виды неопределенностей:

1) 2) 3) 4) 5) 6) 7)

Все эти неопределенности принципиально сводятся к неопределенности вида 2).

Например:

5)-7) сводятся к неопределенности вида 2) логарифмированием.

Замечание 2: обычно при использовании формулы (1) проверка условий 1, 2, 4 практически производится в процессе вычисления. При невыполнении условия 3, которое должно быть проверено до вычисления, можно получить грубейшую ошибку.

Например:

- ошибка

Лекция №13

§7. Исследование функции с помощью производной.

§7.1. Признаки монотонности и постоянства функции. Теорема 1.

Если функция непрерывна на промежутке и производная на , то равна на .

Доказательство:

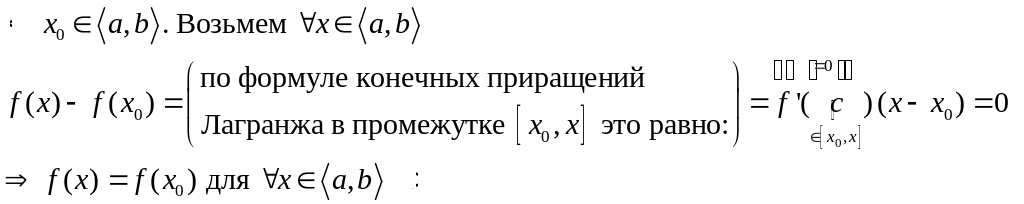
Теорема 2.

Пусть непрерывна на промежутке , тогда:

1. если , то функция возрастает (убывает) на .

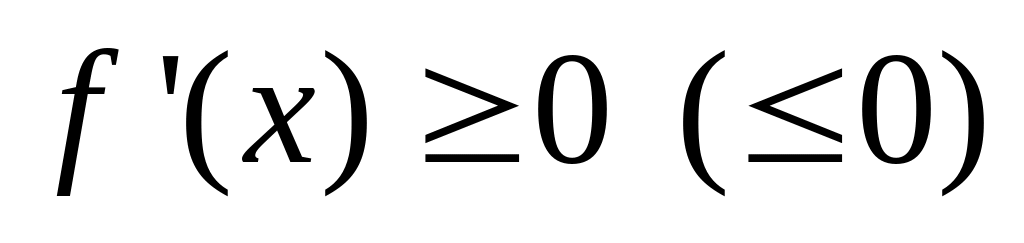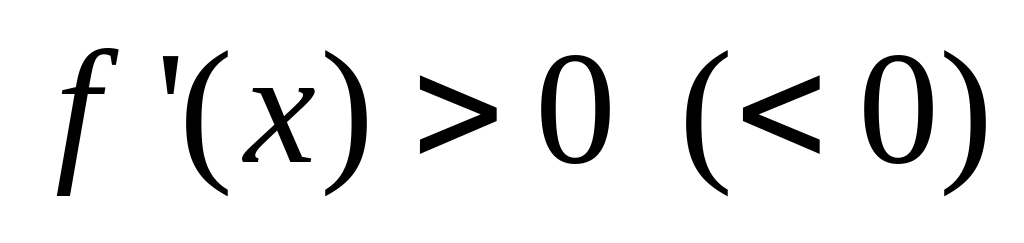2. если , то функция строго возрастает (строго убывает) на .

Доказательство:

для случая возрастания:

Пусть . Возьмем

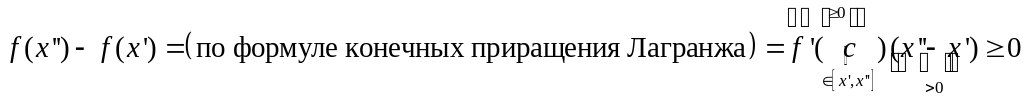
для возрастает.

Геометрический смысл теоремы 2: Если , то касательная везде образует положительный острый угол, т.е. функция идет вверх.

Теорема 3(необходимый признак монотонности)

Если возрастает (убывает) в точке и , то .

Замечание. Из того, что строго возрастает (строго убывает) еще не следует, что , т.е. производная даже строго возрастающей (убывающей) функции может для некоторых значений обращаться в ноль.

§7.2. Экстремум функции.

Пусть функция задана на

Определение 1. Говорят, что во внутренней точке области определения функции функция имеет максимум (минимум), если для . Этот максимум (минимум) называют строгим (собственным), если неравенства строгие.

Замечание. Точки экстремума по определению рассматриваются лишь во внутренних точках. В литературе говорят иногда и о краевых экстремумах.

Необходимый признак экстремума

Теорема.

Если функция имеет экстремум в точке , то либо не существует, либо она равна нулю.

Доказательство:

Если в точке максимум, то по теореме Ферма, если существует в точке , то она равна нулю. Итак, согласно теореме, точки экстремума могут быть лишь в тех внутренних точках, где или не существует. Такие точки называется подозрительными на экстремум. Точка, в которых еще называют стационарными. Не во всякой подозрительной на экстремум точке есть экстремум.

Достаточные признаки экстремума.

Теорема 1(первый достаточный признак)

Пусть -внутренняя точка области определения функции и непрерывна в точке , тогда:

а) если при переходе через точку производная меняет знак с плюса на минус, то в точке максимум.

б) если при переходе через точку производная меняет знак с минуса на плюс, то в точке минимум.

в) если при переходе через точку производная знак не меняет, то в этой точке экстремума нет, т.е. функция в этой же точке монотонна.

Замечание. Требование непрерывности опускать нельзя.