Лекция №1.

§1. Множество вещественных чисел.

§1.1. Понятие вещественного числа и числовая ось.

1)Целые положительные числа(натуральные)-

2)Присоединив к натуральным числам 0 и целые отрицательные числа, получаем множество целых чисел-

3)Присоединив к множеству целых чисел дробные, получаем множество рациональных чисел - . Каждое рациональное число имеет вид , где . Каждое рациональное число может быть записано в виде конечной десятичной или бесконечной периодической десятичной дроби.

4)Все остальные числа иррациональные(бесконечные непериодические дроби)-

(множество вещественных или действительных чисел)

§1.2. Граница числовых множеств.

Определение 1. Число называется верхней(нижней) границей множества A, если для любого элемента выполняется .

Определение 2. Множество называется ограниченным сверху(снизу), если оно имеет верхнюю(нижнюю) границу. Множество называется ограниченным, если оно ограничено и сверху и снизу.

Определение 3. Наименьшее из верхних границ числового множества называется супремумом множества A (sup A). Наибольшее из нижних границ числового множества A называется инфимуом(inf A).Супремум и инфиум называют так же точный верхний и точный нижней границами множества. Они являются обобщением наибольшего и наименьшего элемента.

Свойства точных границ числового множества:

Свойство 1. Критерии sup и inf . Для того чтобы b было точной верхней(нижней) границей числового множества А необходимо и достаточно, чтобы:

1)число b было верхней(нижней) границей числового множества А.

2)

Свойство 2. Основная теорема теории вещественных чисел: всякое ограниченное сверху (снизу) множество А имеет точную верхнюю(нижнюю) границу ( ).

Свойство 3. Для любого непустого множества А выполняется inf A<sup A.

§1.3. Абсолютная величина числа.

Определение. Абсолютной величиной или модулем числа называется число равное самому , если и равное , если .

Свойство абсолютной величины:

Свойство 1.

Свойство 2.

Свойство 3.

Свойство 4.

Свойство 5.

§1.4. Числовая ось.

Определение. Числовой осью называется прямая с выбранным направлением, началом отсчета и единицей длины.

Каждой точке на этой прямой сопоставляется число равное расстоянию от начала отсчета и взятая со знаком + , если точка выбрана в выбранном направлении, и со знаком - ,если точка выбрана в обратном направлении.

-расширенное множество действительных чисел.

Между множеством действительных чисел и числовой прямой существует взаимнооднозначное соответствие. Это значит, что каждому действительному числу соответствует единственная точка на числовой прямой и наоборот, каждая точка на числовой прямой обозначает какое-либо действительное число.

§2. Функции

§2.1. Понятие функции.

Определение. Если каждому элементу по закону или правилу сопоставляется один или несколько элементов , то говорят, что на множестве задана функция со значениями во множестве .

Для каждого элемента множество сопоставимых ему значений обозначается .

Переменную называем аргументов функции или независимой переменной, - значением функции или независимой переменной.

Множество , на которой определена функция называется её областью определения, для -множеством значений функции.

Областью определения функции может быть любое множество области оси. Чаще всего рассматривают следующие случаи(области):

1. Множество целых неотрицательных чисел ( ).

2. Область определения состоит из одних или несколько интервалов(конечных или бесконечных) числовой оси.

Примеры:

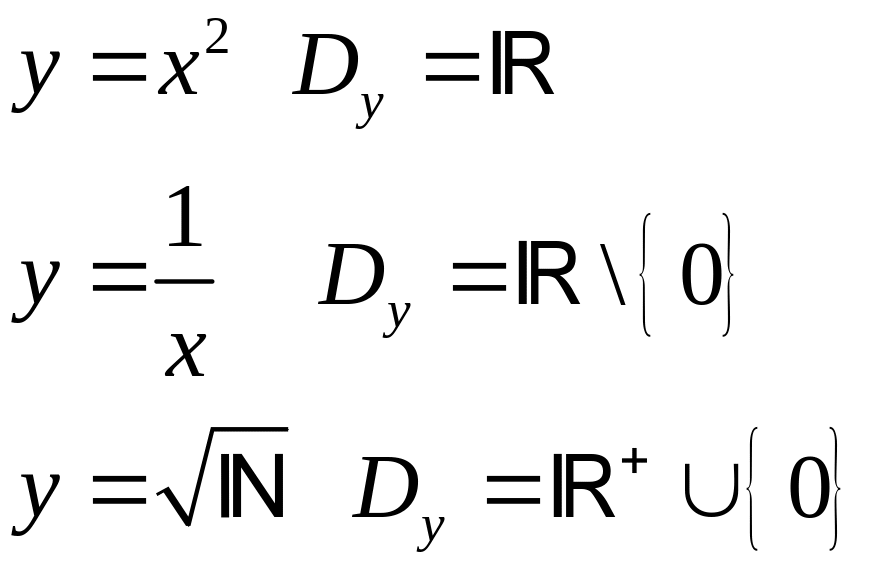
Функции и называются равными, если равны их области определения и для любого значение функции совпадают.

Частный случай функции - это числовая плоскость . Здесь в роли аргумента идет номер члена последовательности (1,2,3,4…), .

Пример:

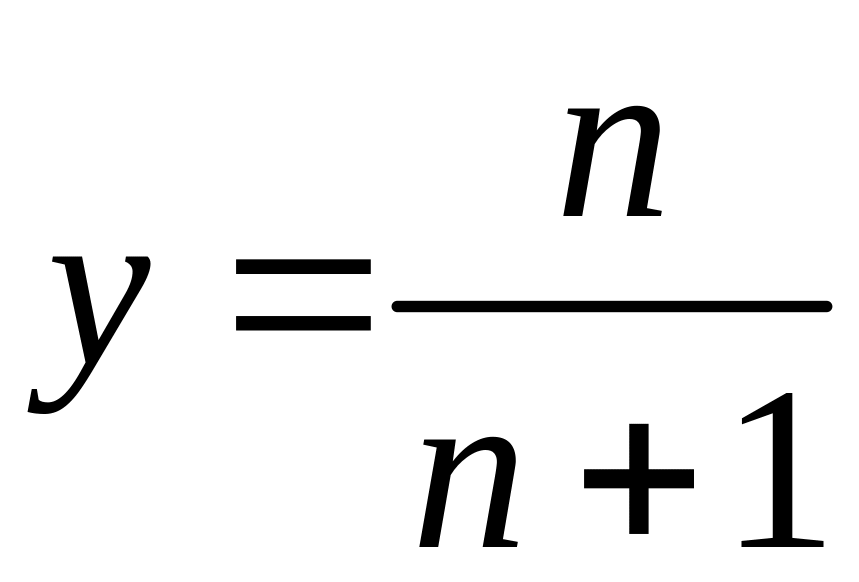
Способы задания функции:

1. Табличный.

2. Аналитический (т.е. с помощью формулы).

3. Графический.