
- •Критерии однородности дисперсии нескольких независимых выборок.
- •Понятие квантили (определение, графическая интерпретация), доверительного интервала, доверительной области. Примеры нахождения квантилей нормального распределения.
- •Критерии однородности выборок. Критерий Смирнова.
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерии однородности выборок. Критерий однородности хи-квадрат Пирсона
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерий проверки значимости линейной регрессии (два подхода).
- •Понятие одномерной и двумерной функции распределения случайного процесса и плотности распределения. Вероятностный смысл.
- •Простые и сложные гипотезы. Статистический критерий различения гипотез. Уровень значимости и мощность критерия. Ошибки первого и второго рода.
- •Числовые характеристики случайных процессов (определение, свойства). Корреляционная теория случайных процессов.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при известной дисперсии.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при неизвестной дисперсии.
- •Доверительные интервалы для математического ожидания нормального распределения.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Сравнение дисперсий двух гауссовских выборок. Критерий Фишера.
- •Интервальный вариационный ряд. Гистограмма частот и относительных частот.
- •Сравнение средних двух гауссовских выборок с равными дисперсиями. Критерий Стьюдента.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •1.Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией.
- •2.Сравнение средних двух гауссовских зависимых выборок.
- •Критерий
- •Понятие статистики как функции от выборки
- •Статистика критерия
- •Оценки максимального правдоподобия параметров нормального распределения.
- •Метод наименьших квадратов для случая квадратичной зависимости и обобщенной линейной зависимости данных.
- •1.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
- •2.Методы линейной регрессии. Метод наименьших квадратов для случая линейной зависимости данных.
- •1.Критерий согласия хи-квадрат Пирсона различения статистических гипотез (случай распределения с неизвестными параметрами).
- •Статистика критерия
- •1.Вариационный ряд. Распределения порядковых статистик выборки (максимальной и минимальной варианты выборки).
- •2.Эмпирическая функция распределения и её свойства. Пример нахождения эмпирической функции и построение ее графика.
- •1.Усиленный закон больших чисел. Теорема Колмогорова и теорема Бореля.
- •2.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
Лемма Неймана — Пирсона. Наиболее мощные критерии
Пусть ![]() -
выборка (набор независимых, одинаково
распределенных величин), и имеются две
гипотезы о распределении
-
выборка (набор независимых, одинаково
распределенных величин), и имеются две
гипотезы о распределении ![]() :
:
![]()
![]()
![]()
![]()
Предполагается, что
распределения ![]() ,
, ![]() либо
оба дискретны, либо оба абсолютно
непрерывны.
либо
оба дискретны, либо оба абсолютно
непрерывны.
Для
любого ![]() НМК
уровня
НМК
уровня ![]() существует
и совпадает с критерием
отношения правдоподобия:
существует
и совпадает с критерием
отношения правдоподобия:
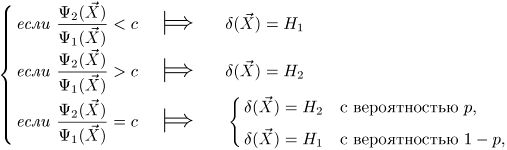
при
этом ![]() и
и ![]() определяются
из уравнения
определяются
из уравнения ![]() ,
или
,
или
![]() (7.1)
(7.1)
Доказательство леммы Неймана - Пирсона
1. Докажем, что уравнение (7.1) разрешимо относительно и .
Рассмотрим
невозрастающую функцию ![]() .
.
![]()
Поскольку
интегрирование ведется по области ![]() ,
то под интегралом
,
то под интегралом ![]() .
Поэтому
.
Поэтому
![]()
![]() при
при ![]() .
.
Рассмотрим ![]() :
:
![]()
Возможны
два критерия:
(а) ![]() и
(б)
и
(б) ![]() .
.
2. Математическое ожидание суммы случайных величин
Докажем,
что для любых двух случайных величин
![]() и
и
![]()
![]() ,
(10.2.3)
,
(10.2.3)
т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Это свойство известно под названием теоремы сложения математических ожиданий.
Доказательство.
а)
Пусть
![]() -
система прерывных случайных величин.
Применим к сумме случайных величин
общую формулу (10.1.6) для математического
ожидания функции двух аргументов:
-
система прерывных случайных величин.
Применим к сумме случайных величин
общую формулу (10.1.6) для математического
ожидания функции двух аргументов:
![]()
![]()
.
Ho![]() представляет
собой не что иное, как полную вероятность
того, что величина
примет
значение
представляет
собой не что иное, как полную вероятность
того, что величина
примет
значение
![]() :
:
![]() ;
;
следовательно,
![]() .
.
Аналогично докажем, что
![]() ,
,
и теорема доказана.
б) Пусть - система непрерывных случайных величин. По формуле (10.1.7)
![]()
![]() .
(10.2.4)
.
(10.2.4)
Преобразуем первый из интегралов (10.2.4):
![]()
![]()
аналогично
![]() ,
,
и теорема доказана.
Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин - как зависимых, так и независимых.
Теорема сложения математических ожиданий обобщается на произвольное число слагаемых:
![]() ,
(10.2.5)
,
(10.2.5)
т. е. математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.
Для доказательства достаточно применить метод полной индукции.
Дисциплина: ТВ и МС Билет № 7
Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при известной дисперсии.
Сравнение двух выборочных средних при известных дисперсиях
Заданы две выборки .
Дополнительные предположения:
обе выборки простые и нормальные;
значения дисперсий
 известны
априори; это означает, что дисперсии
были оценены заранее не по этим выборкам,
а исходя из какой-то другой информации;
случай «неизвестных дисперсий», когда
такого источника информации нет и
дисперсии приходится оценивать по
самим выборкам, описан
ниже.
известны
априори; это означает, что дисперсии
были оценены заранее не по этим выборкам,
а исходя из какой-то другой информации;
случай «неизвестных дисперсий», когда
такого источника информации нет и
дисперсии приходится оценивать по
самим выборкам, описан
ниже.
Нулевая
гипотеза ![]() (средние
в двух выборках равны).
(средние
в двух выборках равны).
Статистика критерия:
![]()
имеет
стандартное Нормальное
распределение ![]() ,
где
,
где
![]() —
выборочные
средние.
—
выборочные
средние.
Критерий (при уровне значимости ):
против альтернативы
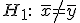
если ![]() ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
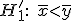
если ![]() ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы

если ![]() ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
где ![]() есть
-квантиль стандартного
нормального распределения.
есть
-квантиль стандартного
нормального распределения.
