Сравнение средних двух гауссовских выборок с равными дисперсиями. Критерий Стьюдента.
Сравнение двух выборочных средних при неизвестных равных дисперсиях
Заданы две выборки .
Дополнительные предположения:
обе выборки простые и нормальные;
значения дисперсий равны:
,
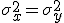но априори не известны.
Нулевая гипотеза (средние в двух выборках равны).
Статистика критерия:
имеет распределение
Стьюдента с 
степенями
свободы, где
— выборочные дисперсии;
— выборочные средние.
Критерий (при уровне значимости ):
против альтернативы
если 
,
то нулевая гипотеза отвергается;
против альтернативы
если 
,
то нулевая гипотеза отвергается;
против альтернативы
если 
,
то нулевая гипотеза отвергается;
где 
есть
-квантиль распределения
Стьюдента с
степенями
свободы.
t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называютгипотезой сдвига).
Все разновидности критерия Стьюдента являются параметрическими и основаны на дополнительном предположении о нормальности выборки данных. Поэтому перед применением критерия Стьюдента рекомендуется выполнить проверку нормальности. Если гипотеза нормальности отвергается, можно проверить другие распределения, если и они не подходят, то следует воспользоваться непараметрические статистические тесты.
Для дальнейшего критического разбора опишем традиционный статистический метод проверки однородности. Вычисляют средние арифметические в каждой выборке
,
затем выборочные дисперсии
, 
и статистику Стьюдента t, на основе которой принимают решение,
Дискретный вариационный ряд. Полигон частот и относительных частот.
В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.
Пусть требуется измерить некоторую величину . Результаты измерений
естественно рассматривать как значения случайных величин , полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить . Следовательно, возникает задача оценить параметр . Для решения задачи рассмотрим случайную величину
Тогда
Это обстоятельство приводит к мысли построить статистические характеристики:
Первая представляет среднее арифметическое наблюденных значений случайной величины и статистическую дисперсию - во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины и к дисперсии
При ограниченности наблюдений эксперимента заменой и на и совершаем погрешность, а при небольшом числе наблюдений величины , являются случайными величинами. Возникает задача об оценке неизвестных параметров , случайной величины на основе экспериментальных данных, т.е. задача - найти подходящие значения этих параметров.
Множество результатов измерений величины называется выборкой объема . Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину рассматривать как случайную величину, функцию распределения которой
следует определить. Полученный статистический материал , , ... наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д.
Если
выборка объема
содержит
различных
элементов
,
причем
встречается
раз,
то число
называется
частотой
элемента
,
а отношение
называется
относительной
частотой
элемента
.
Очевидно, что
Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы ', а вторая - их частоты (относительные частоты .
Полигоном частот (относительных частот) выборки называется ломаная с вершинами в точках ( , , , ).
Функция
,
где
-
объем выборки, а
-
число значений
в
выборке, меньших
,
называется эмпирической функцией
распределения. Функция
служит
оценкой неизвестной функции распределения
,
т.е.
.
Пусть теперь - непрерывная случайная величина с неизвестной плотностью вероятности . Для оценки по выборке разобьем область значений на интервалы длины . Обозначим через середины интервалов, а через число элементов выборки, попавших в указанный интервал. Тогда - оценка плотности вероятности в точке . В прямоугольной системе координат построим прямоугольники с основаниями и высотами , т.е. площади прямоугольника, равной относительной частоте данного разряда. Полученная таким образом фигура называется гистограммой выборки.
Билет № 12
1.t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называют гипотезой сдвига).Все разновидности критерия Стьюдента являются параметрическими и основаны на дополнительном предположении о нормальности выборки данных. Поэтому перед применением критерия Стьюдента рекомендуется выполнить проверку нормальности. Если гипотеза нормальности отвергается, можно проверить другие распределения, если и они не подходят, то следует воспользоваться непараметрические статистические тесты. Пример: Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.
Сравнение двух выборочных средних при неизвестных неравных дисперсиях
Задача сравнения средних двух нормально распределённых выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. Точного решения этой задачи до настоящего времени нет. На практике используются различные приближения.
Заданы две выборки .
Дополнительное
предположение: обе
выборки простые и нормальные.Нулевая
гипотеза
(средние
в двух выборках равны). Статистика
критерия:
где—
выборочные дисперсии;
—
выборочные средние.Критерий (при уровне
значимости 
):против
альтернативы
если 
,
то нулевая гипотеза отвергается; против
альтернативы
если 
,
то нулевая гипотеза отвергается; против
альтернативы
если 
,
то нулевая гипотеза отвергается;где
квантили 
определяются
по-разному в различных приближениях:
Критерий Кохрена-Кокса:
,
где 
есть
-квантиль распределения
Стьюдента с 
степенями
свободы; Критерий Сатервайта:
есть
-квантиль распределения
Стьюдента с числом степеней
свободы 
Критерий
Крамера-Уэлча:
есть
-квантиль распределения
Стьюдента с числом степеней свободы 
2. Сложение случайных функций
Возьмем две случайные функции X(t), Y(t). Пусть известны моменты этих функций до второго порядка включительно:
M[X(t)],M[Y(t)], Kx(t1,t2),Ky(t1,t2) Kxy(t1,t2)
Найдем математическое ожидание случайной функции:
(15) Z(t)=X(t)+Y(t)
В силу линейности операции определения математического ожидания имеем:
(16) M[Z(t)]=M[X(t)]+M[Y(t)]
т.е. математическое ожидание суммы случайных функций равно сумме математических ожиданий этих случайных функций.
Вычитая из равенства (15) равенство (16), получим центрированную случайную функцию:
(17) Z0(t)=X0(t)+Y0(t)
Вычислим корреляционную функцию суммы случайных функций Х(t)+Y(t). По определению корреляционной функции имеем: _____ ____________
(18) Kz(t1, t2)=M[Z0(t1)Z0(t2)]=M[(X0(t1)+Y0(t2)*(X0(t1)+Y0(t2))]=
=Kx(t1, t2)+Kxy(t1, t2)+Kyx(t1, t2)+Ky(t1, t2)
Таким образом, корреляционная функция суммы двух случайных функций равна сумме всех корреляционных и взаимно корреляционных функций этих случайных функций.
Билет №13