2. Доверительные интервалы для дисперсии нормального распределения.

Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Определение

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100p%, порождённым выборкой (x₁,…,x_n), называется интервал с границами l(x₁,…,x_n) и u(x₁,…,x_n), которые являются реализациями случайных величин L(X₁,…,X_n) и U(X₁,…,X_n), таких, что

.

Граничные точки доверительного интервала l и u называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.

Случай известного среднего

Пусть   — независимая выборка из нормального распределения, где μ — известное среднее. Определим произвольное   и построим α — доверительный интервал для неизвестной дисперсии σ².

Утверждение. Случайная величина

имеет распределение χ²(n). Пусть   — α-процентиль этого распределения. Тогда имеем:

.

После подстановки выражения для H и несложных алгебраических преобразований получаем:

.

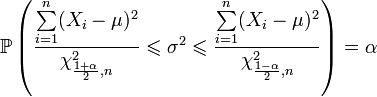Случай неизвестного среднего

Пусть   — независимая выборка из нормального распределения, где μ, σ² — неизвестные константы. Построим доверительный интервал для неизвестной дисперсии σ².

Теорема Фишера для нормальных выборок. Случайная величина

,

где S² — несмещённая выборочная дисперсия, имеет распределение χ²(n − 1). Тогда имеем:

.

После подстановки выражения для H и несложных алгебраических преобразований получаем:

.

Дисциплина: ТВ и МС Билет № 3

1. Критерии однородности выборок. Критерий однородности хи-квадрат Пирсона

Критерии однородности - это критерии проверки гипотез о том, что две (или более) выборки взяты из одного распределения вероятностей. Рассмотрим такую классификацию критериев:

3. Непараметрические (свободные от распределения) критерии однородности не предполагают присутствие какой-либо фундаментальной информации о законе распределения. Любое распределение можно описать параметром положения, характеризующим центр группирования случайных величин, и параметром масштаба, характеризующим степень рассеяния случайных величин относительно центра группирования. Когда закон распределения неизвестен, гипотезы о параметрах проверяются при помощи специальных критериев сдвига и масштаба. Также существуют двухвыборочные критерии согласия.

• Непараметрические критерии сдвига.

Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу. Пусть заданы две выборки ,взятые из неизвестных непрерывных распределений  F(x) и G(y) соответственно

Нулевая гипотеза: 

Наиболее частая альтернативная гипотеза:  .

• Непараметрические критерии масштаба.

Для двух выборок  . проверяется гипотеза о том, что они принадлежат одному и тому же распределению, но с разным параметром масштаба. Если плотность распределения первой выборки —  , а второй выборки —  , то нулевая гипотеза  .

• Двухвыборочные критерии согласия.

4. Если же принимаются какие-либо дополнительные предположения о законе распределения вероятностей, то можно применять параметрические критерии однородности.

Сравнение параметров нормальных распределений

Сравнение двух средних значений

Имеются две выборки независимых случайных величин   Необходимо на основе выборочных данных установить наличие значимой разницы в средних двух совокупностей, из которых извлечены выборки.

Нулевая гипотеза:  .

Альтернативы: 

Сравнение при известных дисперсиях осуществляется при помощи критерия Стьюдента.

Сравнение при неизвестных равных дисперсиях осуществляется при помощи критерия Стьюдента.

Сравнение при неизвестных неравных дисперсиях осуществляется при помощи модификаций критерия Стьюдента: критерий Кохрена-Кокса, Критерий Сатервайта,критерий Уэлча.

Сравнение двух выборочных средних в связанных выборках осуществляется при помощи критерия Стьюдента.

Критерий Уолша ^[1] позволяет проверять гипотезу о принадлежности одного наблюдения нормальному распределению, генерирующему выборку.

Двухступентчатый двухвыборочный медианный критерий Волфа ^[1]

Критерий Фишера для сравнения двух средних с одинаковыми дисперсиями. ^[1] Эквивалентен критерию Стьюдента и основан на связи между распределениями Стьюдента и Фишера.

Сравнение нескольких средних значений

Имеются k выборок из нормально распределенной совокупности 

Нулевая гипотеза 

Альтернатива 

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H₀ о том, что эта случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F ^* (x) исследуемой случайной величины. Сравнение эмпирического распределения F ^* (x) и теоретического (или, точнее было бы сказать, гипотетического - т.е. соответствующего гипотезе H₀) распределения F(x) производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Статистика критерия

Для проверки критерия вводится статистика:

где 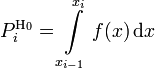  — предполагаемая вероятность попадения в i-й интервал,   — соответствующее эмпирическое значение, n_i — число элементов выборки из i-го интервала, N — полный объём выборки. Также используется расчет критерия по частоте, тогда:

где V_i - частота попадания значений в интервал. Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ².