1.Вариационный ряд. Распределения порядковых статистик выборки (максимальной и минимальной варианты выборки).

Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λm = m / n называется рангом порядковой статистики

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид

Поря́дковые стати́стики в математической статистике - это упорядоченная по возрастанию выборка. Это статистика, занимающая строго определенное место в ранжированной совокупности.

Пусть - конечная выборка из распределения , определённая на некотором вероятностном пространстве . Пусть и . Перенумеруем последовательность в порядке возрастания, так что

Случайная величина X(k)(ω) = x(k) называется k-ой порядковой статистикой исходной выборки.

Очевидно что и

2.Эмпирическая функция распределения и её свойства. Пример нахождения эмпирической функции и построение ее графика.

Выборочная (эмпири́ческая) фу́нкция распределе́ния в математической статистике - это приближение теоретической функции распределения, построенное с помощью выборки из него.

Определение

Пусть   - выборка из распределения случайной величины  , задаваемого функцией распределения  . Будем считать, что  , где  , -независимые случайные величины, определённые на некотором пространстве элементарных исходов Ω. Пусть  . Определим случайную величину  следующим образом:

,

где   - индикатор события  ,   - функция Хевисайда. Таким образом, выборочная функция распределения в точке   равна относительной частоте элементов выборки, не превосходящих значение  . Случайная величина   называется выборочной функцией распределения случайной величины   и является аппроксимацией для функции  . Существует результат, показывающий, что при   функция   равномерно сходится к  , и указывающий скорость сходимости.

Основные свойства

• Пусть зафиксирован элементарный исход 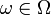 . Тогда 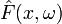  является функцией распределения дискретного распределения, задаваемого следующей функцией вероятности:

,

где x_i = X_i(ω), а   - количество элементов выборки, равных x. В частности, если все элементы выборки различны, то  .

• Математическое ожидание этого распределения имеет вид:

.

Таким образом выборочное среднее - это теоретическое среднее выборочного распределения.

• Аналогично, выборочная дисперсия - это теоретическая дисперсия выборочного распределения.

• Случайная величина 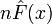  имеет биномиальное распределение:

.

• Выборочная функция распределения   является несмещённой оценкой функции распределения F(x):

.

• Дисперсия выборочной функции распределения имеет вид:

.

• Согласно усиленному закону больших чисел, выборочная функция распределения сходится почти наверное к теоретической функции распределения:

 почти наверное при  .

• Выборочная функция распределения является асимптотически нормальной оценкой теоретической функции распределения. Если 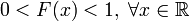 , то

 по распределению при  .

Дисциплина: ТВ и МС Билет № 20