
- •Критерии однородности дисперсии нескольких независимых выборок.
- •Понятие квантили (определение, графическая интерпретация), доверительного интервала, доверительной области. Примеры нахождения квантилей нормального распределения.
- •Критерии однородности выборок. Критерий Смирнова.
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерии однородности выборок. Критерий однородности хи-квадрат Пирсона
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерий проверки значимости линейной регрессии (два подхода).
- •Понятие одномерной и двумерной функции распределения случайного процесса и плотности распределения. Вероятностный смысл.
- •Простые и сложные гипотезы. Статистический критерий различения гипотез. Уровень значимости и мощность критерия. Ошибки первого и второго рода.
- •Числовые характеристики случайных процессов (определение, свойства). Корреляционная теория случайных процессов.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при известной дисперсии.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при неизвестной дисперсии.
- •Доверительные интервалы для математического ожидания нормального распределения.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Сравнение дисперсий двух гауссовских выборок. Критерий Фишера.
- •Интервальный вариационный ряд. Гистограмма частот и относительных частот.
- •Сравнение средних двух гауссовских выборок с равными дисперсиями. Критерий Стьюдента.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •1.Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией.
- •2.Сравнение средних двух гауссовских зависимых выборок.
- •Критерий
- •Понятие статистики как функции от выборки
- •Статистика критерия
- •Оценки максимального правдоподобия параметров нормального распределения.
- •Метод наименьших квадратов для случая квадратичной зависимости и обобщенной линейной зависимости данных.
- •1.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
- •2.Методы линейной регрессии. Метод наименьших квадратов для случая линейной зависимости данных.
- •1.Критерий согласия хи-квадрат Пирсона различения статистических гипотез (случай распределения с неизвестными параметрами).
- •Статистика критерия
- •1.Вариационный ряд. Распределения порядковых статистик выборки (максимальной и минимальной варианты выборки).
- •2.Эмпирическая функция распределения и её свойства. Пример нахождения эмпирической функции и построение ее графика.
- •1.Усиленный закон больших чисел. Теорема Колмогорова и теорема Бореля.
- •2.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
1.Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией.
Обозначим через n объем выборки, по которой найдена исправленная дисперсия S2.
Правило
1.
Для того, чтобы при заданном уровне
значимости α проверить нулевую гипотезу
 о
равенстве неизвестной генеральной
дисперсии
о
равенстве неизвестной генеральной
дисперсии
 гипотетическому(предполагаемому)
значению
гипотетическому(предполагаемому)
значению
 при конкурирующей гипотезе
при конкурирующей гипотезе
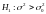 ,
надо вычислить наблюдаемое значение
критерия
,
надо вычислить наблюдаемое значение
критерия
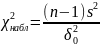 и по табл критических точек распределения
и по табл критических точек распределения
 по
заданному уровню значимости α и числу
степеней свободы κ=n-1 найти критическую
точку
по
заданному уровню значимости α и числу
степеней свободы κ=n-1 найти критическую
точку
 .
Если
.
Если
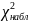 <
<
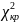 -нет оснований отвергнуть нулевую
гипотезу. Если
>
-нулевую гипотезу отвергают.
-нет оснований отвергнуть нулевую
гипотезу. Если
>
-нулевую гипотезу отвергают.
Правило
2.при
конкурирующей гипотезе
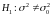 находят
левую
находят
левую
 и правую
и правую
 критические точки. Если
критические точки. Если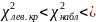
 -
нет оснований отвергнуть нулевую
гипотезу. Если
-
нет оснований отвергнуть нулевую
гипотезу. Если
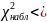
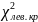 или
>
–
нулевую гипотезу отвергают.
или
>
–
нулевую гипотезу отвергают.
Правило
3.
При конкурирующей гипотезе
 находят критическую точку
находят критическую точку
 .
если
.
если
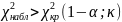 – нет оснований отвергнуть нулевую
гипотезу. Если
– нет оснований отвергнуть нулевую
гипотезу. Если
 –нулевую гипотезу отвергают.
–нулевую гипотезу отвергают.
Замечание.
Если число степеней свободы К>30,то
критическую точку
 )
можно найти из равенства Уилсона-Гильферти:
)
можно найти из равенства Уилсона-Гильферти:
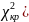 )=κ{1-2/9κ+
)=κ{1-2/9κ+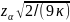 }^3
}^3
,где
 находят, используя функцию Лапласа из
равенства:
находят, используя функцию Лапласа из
равенства:
Ф( )=(1-2α)/2.
2.Сравнение средних двух гауссовских зависимых выборок.
Пусть
генеральные совокупности Х и У
распределены нормально, причем их
дисперсии неизвестны. Из этих совокупностей
извлечены зависимые выборки одинакового
объема n, варианты которых соответственно
равны

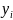 .
Введем следующие обозначения:
.
Введем следующие обозначения:
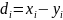 -разности
вариант с одинаковыми номерами,
-разности
вариант с одинаковыми номерами,
d= -
средняя разностей вариант с одинаковыми
номерами,
-
средняя разностей вариант с одинаковыми
номерами,
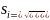 -«исправленное»
среднее квадратичное отклонение.
-«исправленное»
среднее квадратичное отклонение.
Правило
1. Для
того чтобы при заданном уровне значимости
α проверить нулевую гипотезу
 о равенстве 2х средних нормальных
совокупностей Х и У с неизвестными
дисперсиями (в случае зависимых выборок
одинакового объема) при конкурирующей
гипотезе
о равенстве 2х средних нормальных
совокупностей Х и У с неизвестными
дисперсиями (в случае зависимых выборок
одинакового объема) при конкурирующей
гипотезе
 ,
надо вычислить наблюдаемое значение
критерия:
,
надо вычислить наблюдаемое значение
критерия:
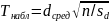
И
по таблице критических точек распределения
Стьюдента, по заданному уровню значимости
α, помещенному в верхней строке таблицы,
и числу степеней свободы κ=n-1 найти
критическую точку
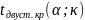 .
Если
.
Если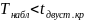 – нет оснований отвергнуть нулевую
гипотезу. Если
– нет оснований отвергнуть нулевую
гипотезу. Если
 –
нулевую гипотезу отвергают.
–
нулевую гипотезу отвергают.
Билет №14
Критерий
В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова — Смирнова) используется для того, чтобы определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.
Критерий Колмогорова — Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных и наиболее широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках.
Обозначим
нулевую гипотезу
![]() ,
как гипотезу о том, что выборка подчиняется
распределению
,
как гипотезу о том, что выборка подчиняется
распределению
![]() . Тогда по теореме Колмогорова для
введённой статистики справедливо:
. Тогда по теореме Колмогорова для
введённой статистики справедливо:
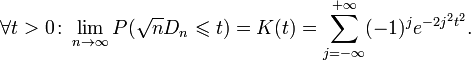
Учтём,
что критерий имеет правостороннюю
критическую область. Если α достаточно
близко к 1, то
![]() можно приблизительно рассчитать по
формуле:
можно приблизительно рассчитать по
формуле:
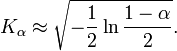 Асимптотическая
мощность критерия равна 1.
Асимптотическая
мощность критерия равна 1.
Обозначим
теперь за нулевую гипотезу
гипотезу о том, что две исследуемые
выборки подчиняются одному распределению
случайной величины
![]()
Теорема Смирнова.
Пусть
![]() — эмпирические функции распределения,
построенные по независимым выборкам
объёмом n и m случайной величины ξ. Тогда,
если
— эмпирические функции распределения,
построенные по независимым выборкам
объёмом n и m случайной величины ξ. Тогда,
если
![]() , то
, то
![]() , где
, где
![]()
Статистика
Эмпирическая
функция распределения (ЭФР)
![]() случайной величины
случайной величины
![]() , построенная по выборке
, построенная по выборке
![]()
![]() , имеет вид:
, имеет вид:
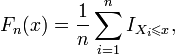 где
где
![]() указывает, попало ли наблюдение Xi в
область :
указывает, попало ли наблюдение Xi в
область :
![]()
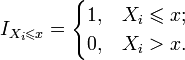
Статистика
критерия для эмпирической функции
распределения
![]() определяется следующим образом:
определяется следующим образом:
![]()
где
![]() — точная верхняя грань множества
— точная верхняя грань множества
![]() , F - предполагаемая модель.
, F - предполагаемая модель.
Теорема Колмогорова
Пусть
![]() — бесконечная выборка из распределения,
задаваемого непрерывной функцией
распределения F. Пусть
— бесконечная выборка из распределения,
задаваемого непрерывной функцией
распределения F. Пусть
![]() — выборочная функция распределения,
построенная на первых n элементах
выборки. Тогда
— выборочная функция распределения,
построенная на первых n элементах
выборки. Тогда
![]() по распределению при
по распределению при
![]() , где K — случайная величина, имеющая
распределение Колмогорова.
, где K — случайная величина, имеющая
распределение Колмогорова.
Замечание
Неформально
говорят, что скорость сходимости
выборочной функции распределения к её
теоретическому аналогу имеет порядок
![]()
Правило (непараметрический критерий Колмогорова).
Если
статистика
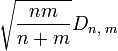 превышает квантиль распределения
Колмогорова
заданного уровня значимости
превышает квантиль распределения
Колмогорова
заданного уровня значимости
![]() ,
то нулевая гипотеза
(об однородности выборок) отвергается.
Иначе гипотеза принимается на уровне
.
,
то нулевая гипотеза
(об однородности выборок) отвергается.
Иначе гипотеза принимается на уровне
.
