
- •1.Неустановившееся движение упругой жидкости в упругой пористой среде
- •1.1.Особенности проявления упругого режима
- •1.2.Упругий запас
- •1.3.Дифференциальное уравнение упругого режима
- •1.4.Точные решения некоторых задач упругого режима
- •1.4.1.Приток упругой жидкости к галерее при постоянном перепаде давлений
- •1.4.2.Приток упругой жидкости к галерее при постоянном расходе
- •1.4.3.Приток упругой жидкости к скважине при постоянном расходе. Основная формула теории упругого режима
- •1.5.Интерференция скважин и в условиях упругого режима
- •1.6.Расчет распределения давления при переменном во времени расходе или давлении на забое
- •1.7.Исследование скважин на нестационарных режимах
- •1.8.Приближенные методы решения задач упругого режима
- •1.8.1.Метод последовательной смены стационарных состояний
- •1.8.2.Приток упругой жидкости к с постоянным расходом
- •1.8.3.Приток упругой жидкости к галерее с постоянным давлением
- •1.8.4.Приток упругой жидкости к скважине с постоянным расходом
- •1.9.Примеры и задачи
- •2.Неустановившаяся фильтрация газа в пористой среде
- •2.1.Дифференциальное уравнение неустановившейся фильтрации газа в пористой
- •2.2.Нестационарный Приток газа к скважине работающей с постоянным расходом
- •2.3.Исследование газовых скважин на нестационарных режимах
- •2.4.Примеры и задачи
- •3.Взаимное вытеснение несмешивающихся жидкостей.
- •§ 1. Связь с проблемой нефтегазоотдачи пластов
- •3.1.Обобщенный закон Дарси
- •3.2.Капиллярное давление
- •3.3.Уравнение неразрывности несмешивающих жидкостей
- •3.4.Теория Баклея - Леверетта
- •3.5.Примеры и задачи
- •4.Гидродинамические методы повышения нефте- и газоотдачи пластов
- •5.Программа курса “Подземная гидромеханика”
- •6.Контрольные задания
- •7.Приложения
- •7.1.Интеграл вероятности
- •Оглавление
- •1. Неустановившееся движение упругой жидкости в упругой пористой среде 1
3.4.Теория Баклея - Леверетта
В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание.
Для обоих случаев одномерного потока (прямолинейно–параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта.
Рассмотрим пласт толщиной h и длиной L Рис. 3.5. Слева, за границей нефтяного пласта, находится законтурная вода. Из пласта происходит отбор нефти с постоянным расходом Qo. Вода и нефть считается несжимаемыми. В законтурной области водонасыщенность равна единице, а в нефтяном пласте додонасыщенность равна остаточной водонасыщенности во. Необходимо рассчитать распределение водонасыщенности с различные моменты времени.
Р |
Эта задача иписывается уравнениями неразрывности:
|
(3.0) |
И обобщенным законом Дарси:
|
(3.0) |
Сложим уравнения неразрывности. Сумма насыщенностей равна единице, поэтому:
|
(3.0) |
При интегрировании последнего уравнения учтем, что жидкости несжимаемые, поэтому расход отбора нефти равен расходу закачки воды. При плоско параллельном движении будут равны и скорости. Обозначим скорость внедрения воды через uo = Qo/(B h). Тогда:
|
(3.0) |
Подставим скорости фильтрации, найденные из обобщенного закона Дарси в последнее уравнение:
|
(3.0) |
Найдем из последнего уравнения градиент давления и подставим его в обобщенного закона Дарси для воды:
|
(3.0) |
Здесь через f(в) обозначена функция Баклея - Леверетта
|
(3.0) |
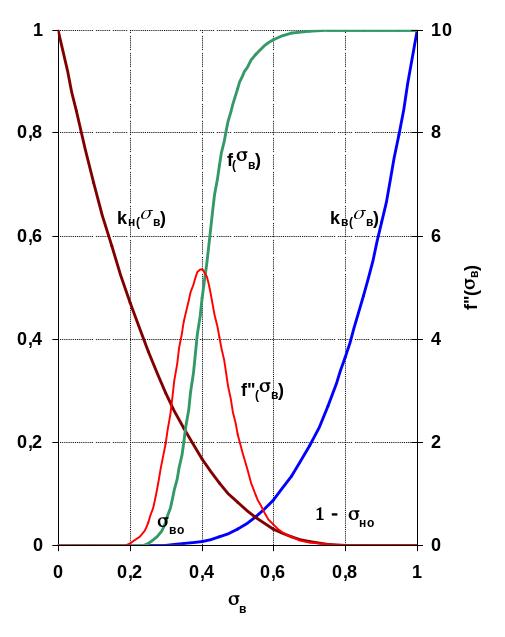
Функция Баклея—Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту. Задачи повышения нефте – и газоконденсатоотдачи в значительной степени сворятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции Баклея – Леверетта в направлении увеличения полноты вытеснения.
Типичные графики функции Баклея – Леверетта и ее производной f '(в) изображены на рис. 3.6. С ростом насыщенности f(в) монотонно возрастает от 0 до 1. Характерной особенностью графика f(в) является наличие точки перегиба, участков вогнутости и выпуклости, где вторая производная f ''(в) соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта.
Р |
Для нахождения распределения водонасыщенности по пласту подставим скорость фильтрации воды ( 3 .0) в уравнение неразрывности для воды:
|
(3.0) |
Считая, что водонасыщенность зависит от координаты x, получим:
|
(3.0) |
f '(sв) – производная от функции Баклея – Леверетта по водонасыщенности.
Решение этого уравнения первого порядка в частных производных имеет вид:
|
(3.0) |
Это решение математически справедливо рис. 3.7, но физически выполняется не для всех значений насыщенности. Из рисунка видно, что в каждой точке пласта будут три значения насыщенности, что абсурдно.
Р |
Физической особенностью модели двухфазного вытеснения Бакалея - Леверетта является зависимость скорости фильтрации воды от значения насыщенности. Действительно, из формулы ( 3 .0) и графика зависимости функции Бакалея – Леверетта от водонасыщенности следует рисунок 3.7, что с ростом водонасыщенности скорость фильтрации воды сначала растёт, а потом уменьшается.
Условия на скачках насыщенности
Положение скачков (разрывов) насыщенности заранее неизвестно и должно быть найдено в зависимости от времени из решения задачи. Оказывается, что значения насыщенности и до - и после + разрыва соответственно не могут быть произвольными, а связаны друг с другом и скоростью разрыва определенными соотношениями. Несмотря на то что дифференциальное уравнение ( 3 .0), выражающее баланс массы каждой фазы, в точках образовавшегося разрыва они теряют физический смысл, так, как производные по координате и по времени равны бесконечности.
Рассмотрим наиболее простой случай скачка, когда водонасыщенность до скачка равна остаточной водонасыщенность - = во, а после скачка фронтальной водонасыщенности, которая неизвестна, но не меняется с течением времени + = вф. Считая, что площадь поперечного сечения равен единице, объём закачки воды в пласта равен скорости закачки воды , а объём изменения воды в пласта равен изменению водонасыщенности в пласте умноженной на координату проникновения воды в пласт, которую можно представить в виде:
|
(3.0) |
xф – координата фронта, м;
x – текущая координата положения при насыщенности в.
Используя формулы для положения координат точек с данной насыщенностью, получим:
|
(3.0) |
Интегрируя и исключая постоянные множители, получим:
|
(3.0) |
Так, как при водонасыщенности равной единице функции Бакалея – Леверетта равна нулю, получаем уравнение:
|
(3.0) |
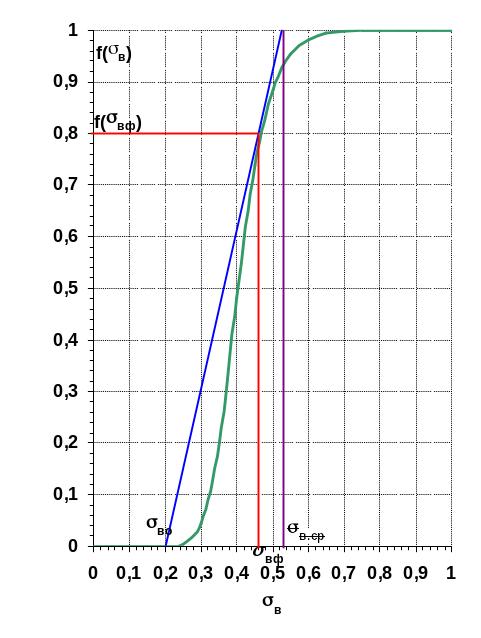
Аналитическое решение последнего уравнения затруднительно, но имеет простой геометрический смысл. Оно представляет собой уравнение касательной, проведенной из точки остаточной водонасыщенности, к кривой функции Бакалея – Леверетта, рисунок 3.8. Это дает простой графический способ определения фронтовой насыщенности по известной функции Баклея—Леверетта, который в некоторых случаях может заменить решение трансцендентного уpaвнения ( 3 .0).
Р |
Важным показателем процесса вытеснения служит средняя водонасыщенность а в зоне смеси за фронтом вытеснения, определяемая как отношение объема воды в пласте после ее закачки, к объему порового пространства в зоне смеси. Средняя водонасыщенность в.ср = определяется по формуле:
|
(3.0) |
Графический способ определения средней водонасыщенности за фронтом – продолжить касательную к функции Баклея—Леверетта до точки, где функции Баклея—Леверетта равна единице. Тогда абцисса этой точки равна средней водонасыщенности за фронтом.
Равенство (9.58) имеет простую геометрическую интерпретацию. Если продолжить касательную к кривой / (а) (см. рис. 9.4), определяющую фронтовую насыщенность ас, до пересечения в точке В с прямой / (а) = 1, то абсцисса точки В определит значение а.
Необходимо отметить, что в действительности математический скачок насыщенности не имеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счет которых появляется некоторая «переходная зона» вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно от значения ас до а„ (см. § 6).
Расчет коэффициента нефтеотдачи
Одна из важных технологических характеристик процесса вытеснения — коэффициент безводной нефтеотдачи . Он определяется как отношение вытесненного водой объема нефти от нагнетательной галереи до фронта к общему объему пор, занятых нефтью до начала вытеснения. Тогда:
|
(3.0) |
Коэффициент безводной нефтеотдачи увеличивается с ростом отношения вязкостей воды к нефти, то есть при увеличении вязкости вытесняющей фазы или (и) при уменьшении вязкости вытесняемой фазы.
Полученные точные решения задачи о вытеснении нефти водой применяются при оценочных инженерных расчетах основных технологических параметров разработки нефтяных и газовых месторождений с использованием процесса заводнения. Кроме того, они могут служить тестами при оценке точности численных методов решения более сложных задач двухфазной фильтрации с использованием ЭВМ.
В общем случае неодномерного вытеснения, а также при учете сжимаемости одной из фаз рассмотренная задача уже не сводится к одному уравнению для насыщенности. Необходимо совместно определять давление и насыщенность. Численные решения таких задач могут быть получены лишь на ЭВМ.

 ис.
3.21. Схема пласта и
начальное распределение водонасыщенности
ис.
3.21. Схема пласта и
начальное распределение водонасыщенности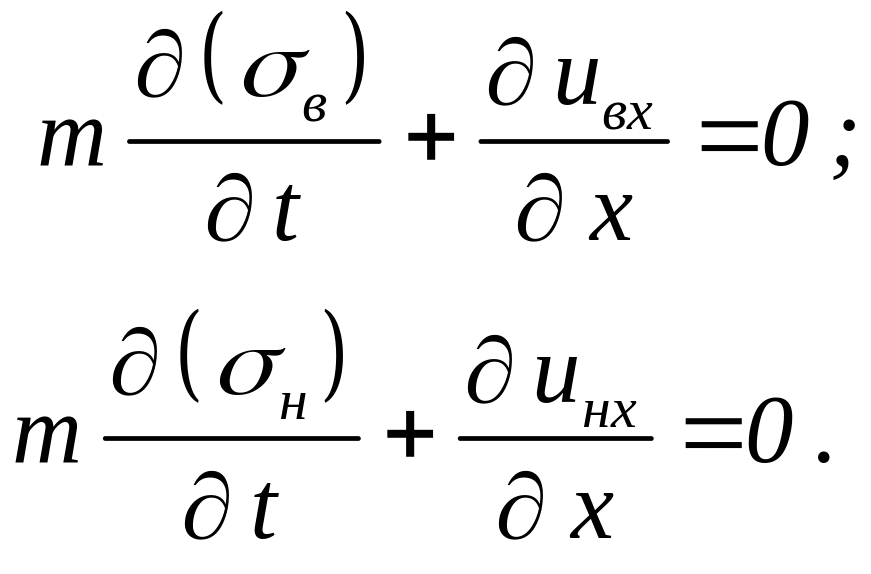
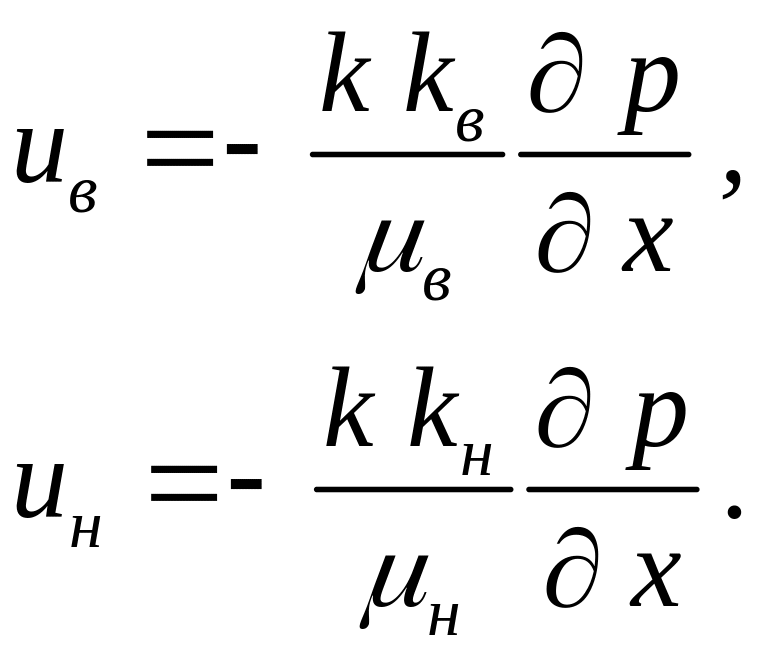 .
.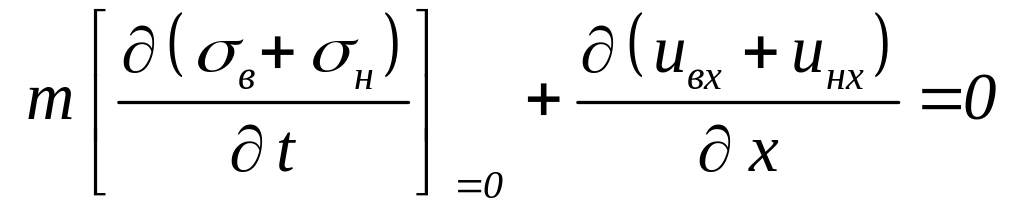 .
.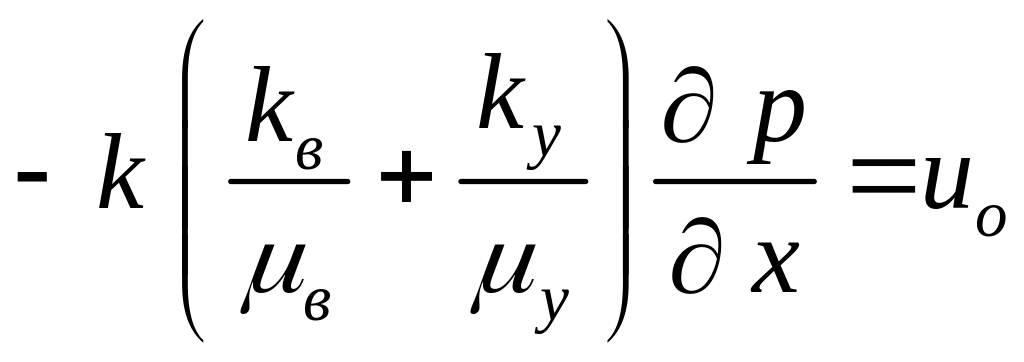 .
.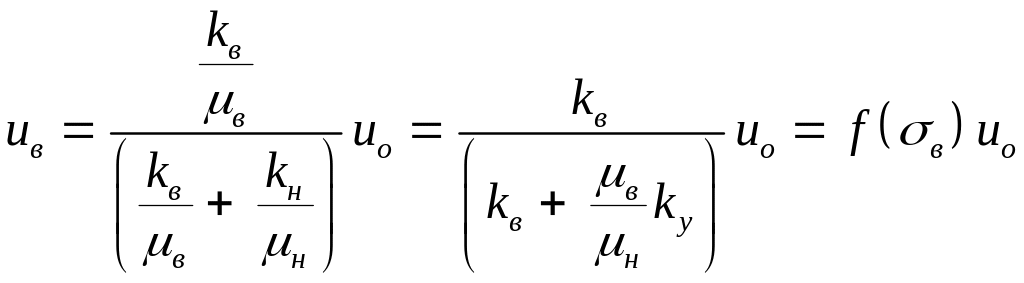 .
.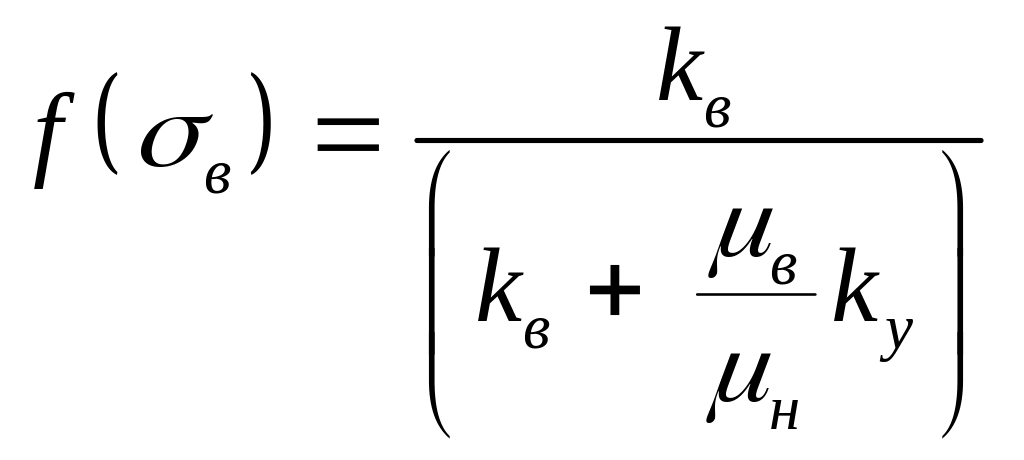 .
. ис.
3.22. Типичные графики
функции Баклея - Леверетта и ее
производной
ис.
3.22. Типичные графики
функции Баклея - Леверетта и ее
производной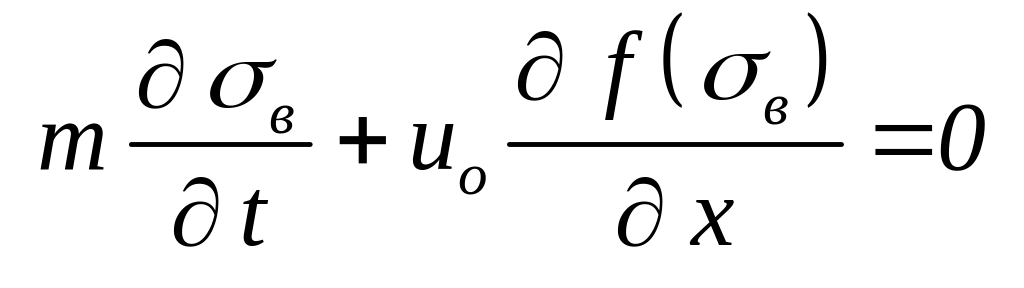 .
.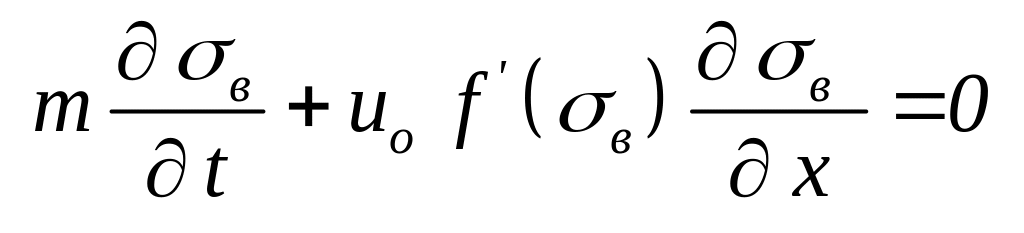 .
.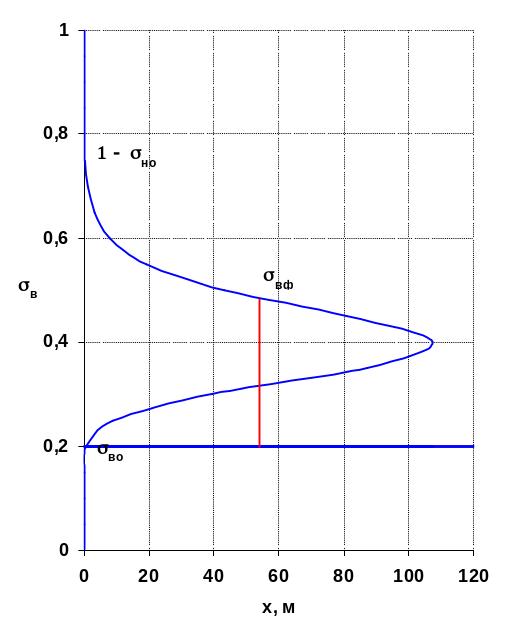 ис.
3.23. Распределение
водонасыщенности по длине пласта
ис.
3.23. Распределение
водонасыщенности по длине пласта .
.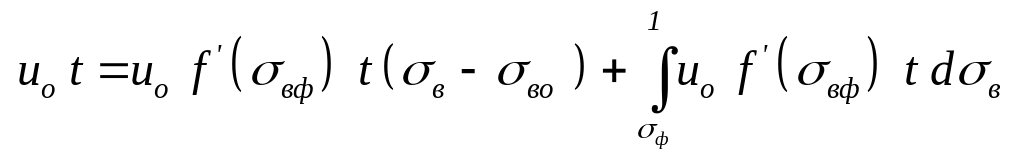 .
.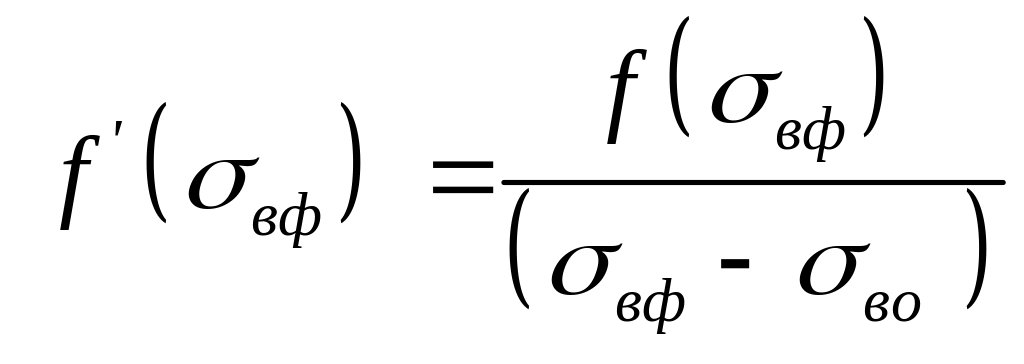 .
. ис.
3.24. Графический способ
определения фронтовой и средней
водонасыщенности
ис.
3.24. Графический способ
определения фронтовой и средней
водонасыщенности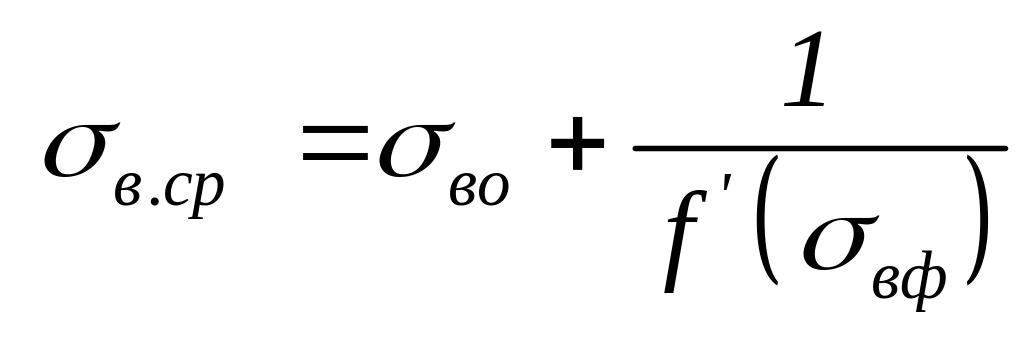 .
.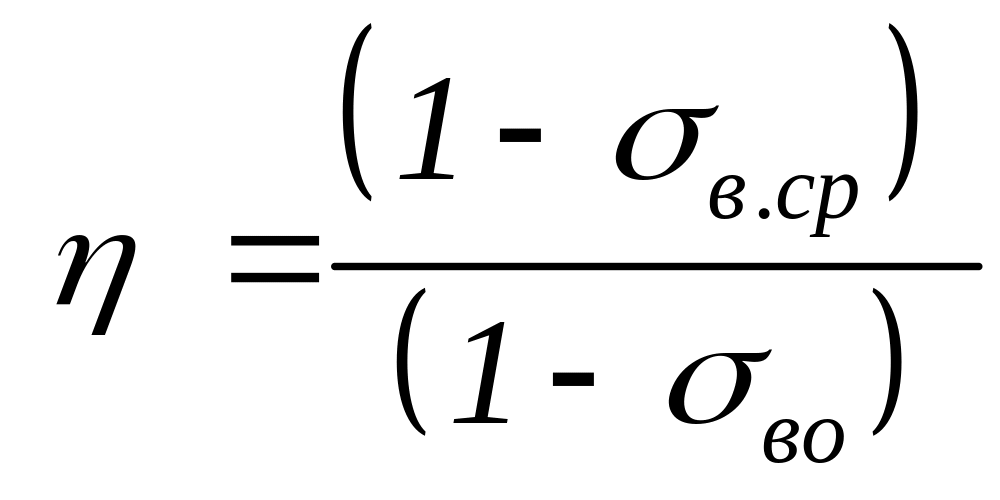 .
.