29) Двойной интеграл в полярных координатах. Вычисление двойного интеграла в полярных координатах

Пусть кривая АВ задана уравнением в полярных координатах . Предположим, что и непрерывны на отрезке Если и равенствах , связывающих полярные и Декартовы координаты, параметром считать угол φ то кривую АB можно задать параметрически Тогда Поэтому

Применяя формулу (41.5), получаем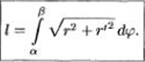

3 0) Масса неоднородного тела. Тройной интеграл.

Тройной интеграл(ТИ) – предел последовательности интегральных сумм построенных по последовательности разбиений тела Т, в которой максимальный диметр частичного тела равен нулю.

Если U=f(x,y,z) непрерывна во всех точках тела Т и его границах, то всякая последовательность интегральных сумм имеет предел и он является одним и тем же для всех последовательностей интегральных сумм его называют тройным интегралом от функции f(x,y,z) области Т.

Пусть дано тело произвольной формы. Рассмотрим некоторую точку этой фигуры массой ∆m объемом ∆V. Средней объемной плотностью называют отношение ρ=∆m/∆V. Плотностью фигуры в данной точке называется предел отношения средней плотности при условии, что частичная площадка стягивается в точку. Масса фигуры вычисляется по формуле

31) Вычисление тройного интеграла в декартовых координатах: повторный и троекратный интеграл.

Тело Т называется правильным в направлении оси OZ, если всякая прямая проходящая через любую внутреннюю точку проекции тела Т на плоскость XOY и параллельная оси Z, пересекает границу тела Т не более чем в 2 точках.

Правильное тело ограничивается снизу и сверху двумя поверхностями которые являются функциями 2 переменных.

Е сли тело Т является правильным в направлении оси OZ и если подынтегральная функция f(x,y,z) непрерывна в этом теле и на ее границы то ТИ по этому телу выражается через ДИ следующим образом:

где D проекция тела Т на XOY

φ1(x,y), φ2(x,y) задают верхнюю и нижнюю границы тела

32) Замена переменных в тройном интеграле

Для тройного интеграла имеет место следующее правило замены переменных. Если функция непрерывна в замкнутой области V, а функции (1)имеют непрерывные частные производные в замкнутой области Т пространства UVW и взаимно однозначно отображают эту область на область V пространства XYZ, то имеет место следующая формула:

(2)

где 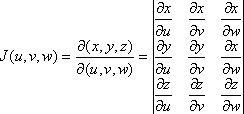- якобиан отображения

Подобно тому как в случае двух переменных модуль якобиана отображения равнялся коэффициенту изменения бесконечно малой площади, модуль якобиана отображения (1) равен коэффициенту изменения бесконечно малого объема при отображении (1).

П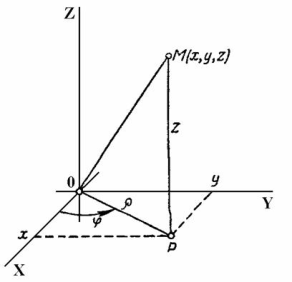 римечание. Формула (2) остается справедливой также и в том случае, если отображение области T на область V взаимно однозначно лишь для внутренних точек этих областей.