12) Линейные неоднородные дифференциальные уравнения второго порядка.

Уравнение вида y"+py'+qy=f(x), где р и q — вещественные числа, f(x) — непрерывная функция, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами. Общее решение уравнения представляет собой сумму частного решения неоднородного уравнения н общего решения соответствующего однородного уравнения. Нахождение общего решения однородного уравнения изучено. Для нахождения частного решения воспользуемся методом неопределенных коэффициентов, не содержащим процесса интегрирования.

Метод вариации произвольной постоянной. Этот метод основан на том, что форма записи решения неоднородного уравнения такая же, что и у соответствующего однородного, с той лишь разницей, что произвольную постоянную С следует считать некоторой функцией переменной t, С = С(t), то есть x(t)=C(t)e (3.5) Функция C(t) должна быть такой, чтобы при подстановке (3.5) в уравнение (3.1) последнее обращалось в тождество. Подставляя x(t) и C'(t)e =f(t) или C'(t)=f(t)e Интегрируя, находим выражение для C(t): (3.6)Подставляя полученное выражение в (3.4), получаем общее решение линейного неоднородного уравнения (3.1) в виде . (3.7) Заметим, что первое слагаемое в формуле (3.7) является частным решением линейного неоднородного уравнения (3.1), в чем можно убедиться не­посредственной проверкой. Второе слагаемое является общим решением соответствующего однородного уравнения (3.3). Этот результат подтверждает известное свойство решений неоднородного уравнения. Приведенные рассуждения позволяют сформулировать алгоритм решения уравнения (3.1).

13) Линейное неоднородное уравнение второго порядка с постоянными коэффициентами.

Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения

и некоторого частного решения неоднородного. Вид частного решения неоднородного уравнения в некоторых конкретных случаях

1. - многочлен степени m:

а) число 0 не является корнем характеристического уравнения  , т. е.  , тогда

где   - многочлен порядка m;

     б) число 0 - корень характеристического уравнения, т. е. b = 0, тогда

если 0 - простой корень, т. е.  ;

если 0 - кратный корень, т. е. a = 0.

10) Линейные однородные диф уравнения 2 порядка. Общее решение. Определитель Вронского. Условия независимости.

Дадим признак линейной независимости n частных решений (11.3) однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка n – 1 включительно:

W(x) = 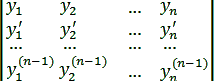Этот определитель называется определителем Вронского решений y₁, y₂, …, y_n. Теорема. Для того чтобы решения (11.3) были линейно независимы в (a, b), т. е. в интервале непрерывности коэффициентов уравнения L(y) = 0, необходимо и достаточно, чтобы W(x) не обращался в нуль ни в одной точке из (a, b).

Линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:

и установим некоторые свойства его решений.

Теорема. Если функции y₁=y₁(x) и у₂=у₂(х) являются частными решениями уравнения (3.13), то решением этого уравнения является также функция где c₁ и с₂ - произвольные постоянные.