14) Функции двух переменных

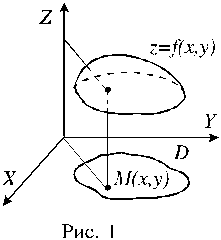
Пусть имеется n+1 переменная x₁,x₂,...,x_n,y, которые связаны между собой так, что каждому набору числовых значений переменных x₁,x₂,...,x_n соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x₁,x₂,...,x_n называется значением функции f в точке (x₁,x₂,...,x_n),что записывается в виде формулы y=f(x₁,x₂,...,x_n) или y=y(x₁,x₂,...,x_n). Переменные x₁,x₂,...,x_n являются аргументами этой функции, а переменная y ‑ функцией от n переменных. Аргументы функции двух переменных будут обозначаться, как правило, x и y, а значение функции - z. Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f(x,y) и называется значением функции f в точке (x,y). Множество D называется областью определения функции. В связи с этим определение.

Переменная z называется функцией двух переменных f(x,y), если для любой пары значений (x,y) Î D ставится в соответствие определенное значение переменной z.

Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами функции будут координаты x,y точки M.

Числа x,y можно рассматривать как координаты вектора  , исходящего из начала координат и с концом в точке M(x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f( ), причем аргументами функции являются координаты вектора  .

График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)ÎD. График представляет собой некоторую поверхность. Предел функции. Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенству называется d-окрестностью точки М₀(х₀;у₀). Другими словами, d-окрестность точки М_о — это все внутренние точки круга с центром М_о и радиусом 8 (см. рис. 206).

Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М₀(х₀;у₀), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х₀ и у → у₀ (или, что то же самое, при М(х; у) → М₀(х₀; у₀)), если для любого є > 0 существует d > 0 такое, что для всех х ≠ х₀ и у ≠ у₀ и удовлетворяющих неравенству

 выполняется неравенство | ƒ (х; у) — А| < є. Записывают:

Непрерывность функции двух переменных в точке

Пусть f – функция двух переменных и M₀(x₀,y₀) – предельная точка множества D(f), принадлежащая этому множеству. Тогда функция fназывается непрерывной в точке M₀, если:

.

Переходя к координатным обозначениям M₀=(x₀,y₀), M=(x,y), мы можем аналогично случаю функции одной переменной, рассматривать разности x-x₀, y-y₀как приращение аргументов ∆x и ∆y, а разность f(x,y)- f(x₀,y₀) – как приращение функции ∆ f(x₀,y₀). Тогда получаем, что функция  f непрерывна в точке (x₀,y₀), если бесконечно малым приращениям аргументов ∆x и ∆y соответствует бесконечно малое приращение функции ∆ f(x₀,y₀), т. е.  . Теперь учитывая определение предела функции в точке, переформулируем определение непрерывности.

Определение 7. Функция f называется непрерывной в точке M₀, если M₀ÎD(f) и для любой точки M_n, принадлежащей D(f) выполняется условие:

.

Следовательно, функция является непрерывной в точке, если: 1. функция определена в этой точке; 2. имеет предел в этой точке; 3. предел равен значению функции в этой точке. В противном же случае функция терпит разрыв в этой точке.