4.Числовая последовательность, ее предел. Свойства пределов.

Если заменить каждое натуральное число  n  в этом ряду некоторым числом  u_n , следуя некоторому закону, то мы получим новый ряд чисел:          

 

u₁ ,   u₂ ,   u₃ , …,   u_n  1 ,   u_n  , …,  кратко обозначаемый { u_n }  

 

и называемый числовой последовательностью. Величина  u_n называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой  u_n = f ( n ), позволяющей найти любой член последовательности по его номеру  n ;эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).

 

П р и м е р ы    числовых последовательностей:

 

                         1,  2,  3,  4,  5, …   ряд натуральных чисел ;

 

                         2,  4,  6,  8,  10, …  ряд чётных чисел;

 

                         1.4,  1.41,  1.414,  1.4142, …  числовая последовательность

                                                                            приближённых  значений 

                                                                            с увеличивающейся точностью.

Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу  a  при увеличении порядкового номера  n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.

Некоторые замечательные пределы:

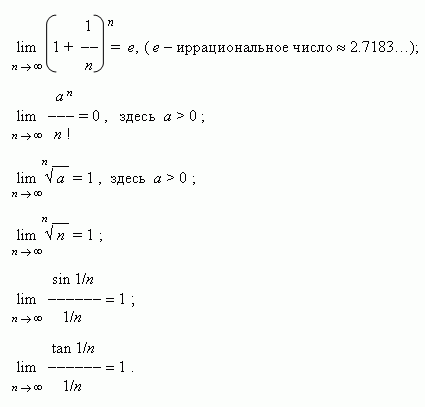
• Свойства пределов

• Предел 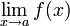  единственнен, то есть

• Сходящаяся функция локально сохраняет знак. Более обще,

где   - проколотая окрестность точки a.

• В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

• Сходящаяся функция локально ограничена в окрестности предельной точки:

• Операция взятия предела сохраняет нестрогие неравенства.

• Предел суммы равен сумме пределов:

• Предел разности равен разности пределов:

• Предел произведения равен произведению пределов:

• Предел частного равен частному пределов.

5. Предел функции. Свойства пределов.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: