35. Задачи на наибольшее и наименьшее значение функций

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, анаименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:

1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

2. Вычислить значения функции на концах отрезка при x = a, x = b.

3. Из всех полученных значений выбрать наибольшее и наименьшее.

Примеры.

1. Найти наибольшее и наименьшее значения функции 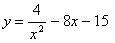  на отрезке [–2; –0,5].

Найдем критические точки функции. 

Вычислим значения функции в найденной точке и на концах заданного отрезка.

Итак, 

2. Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].

36. Понятие первообразной. Неопределённый интеграл. Его свойства

Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция   является первообразной  . Так как производная константы равна нулю,   будет иметь бесконечное количество первообразных;

Неопределённый интегра́л для функции   — это совокупность всех первообразных данной функции.

Если функция   определена и непрерывна на промежутке   и   — её первообразная, то есть   при  , то

  ,

где С — произвольная постоянная.

интегралы от основных элементарных ф-ий.

Произв. от неопр. интеграла равна подинтегр. ф-ии.

Диференциал неопр. интеграла равен подинтегр. выражению

Неопред. интеграл от диференциала некотор. ф-ии равен этой ф-ии с точностью до постоянного слогаемого

Постоянный множитель можно выносить за знак интеграла.

Интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих ф-ий.

Табличные интегралы

37. Метод замены переменной в неопределенном интеграле

См.тетрадку.

38. Метод интегрирования по частям в неопределенном интеграле

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

39.Интегрирование простейших рациональных дробей

См.тетрадь+там примеры.

40. Интегрирование тригонометрических функций

1.Интегралы вида       вычисляются преобразованием произведения тригонометрических функций в сумму по формулам:

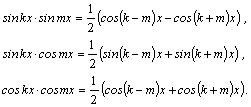
Например, 

2.Интегралы вида , где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала.

Например,

3.Интегралы вида  , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:

Например,

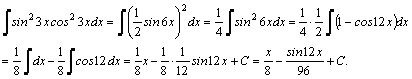
4.Интегралы   где  вычисляются заменой переменной: или

Например,

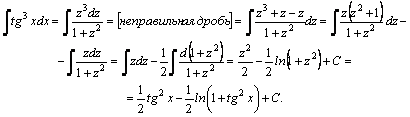
5.Интегралы вида   сводятся к интегралам от рациональных дробей с помощью универсальной тригонометрической подстановки  тогда 

 (т.к. =[после деления числителя и знаменателя на  ]= ;

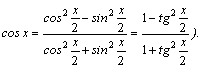
Например,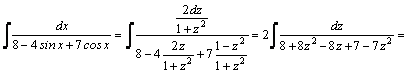 

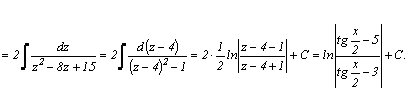
Следует заметить, что использование универсальной подстановки нередко приводит к громоздким выкладкам.