41. Интегрирование иррациональных выражений

См.конспект.

42. Определённый интеграл. Определение. Геометрический смысл

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция илифункционал, а вторая — область в множестве задания этой функции (функционала).

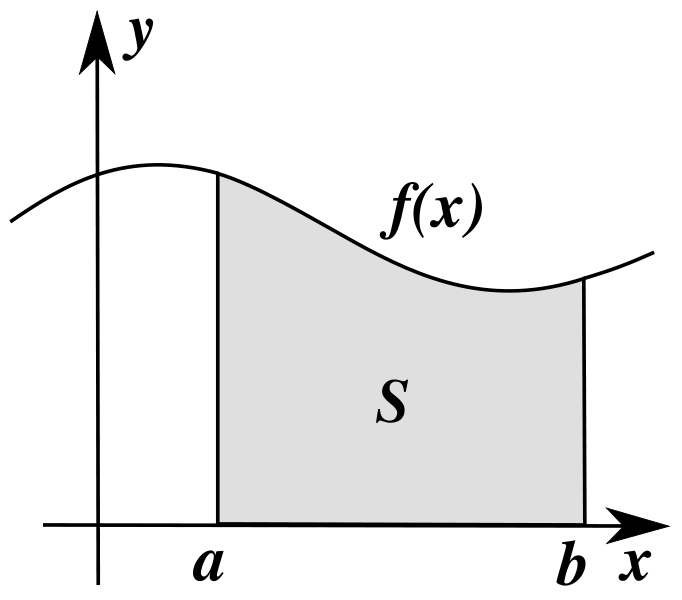
Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение R отрезка [a;b]Далее выберем произв. точку  , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при  , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.   (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

• 

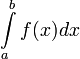
• a – нижний предел.

• b – верхний предел.

• f(x) – подынтегральная функция.

• λ_R - длина частичного отрезка.

• σ_R – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

• λ_R - максимальная длина част. отрезка.

Определение интеграла на языке  , δ:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx

Определённый интеграл   численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

43. Определённый интеграл. Свойства

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

44. Интеграл с переменным верхним пределом

Пусть на отрезке [ a, b ] задана непрерывная функция  f ( x ), тогда для любого x   [ a, b ] существует функция: 

задаваемая  интегралом с переменным верхним пределом, стоящим в правой части равенства.

 

На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.

П р и м е р .

Переменная сила на прямолинейном пути изменяется по закону:   f ( x ) = 6x2 + 5 при  x   0. По какому закону изменяется работа этой силы ?

Р е ш е н и е.

Работа силы  f ( x ) на отрезке [ 0 , x ] прямолинейного пути равна: 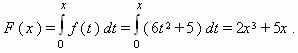  Таким образом, работа изменяется по закону:  F ( x ) = 2x 3 + 5x .

Из определения  интеграла с переменным верхним пределом - функции F ( x ) и известных свойств интеграла следует, что при  x   [ a , b]

 

F' ( x ) = f ( x ) .