6. Затухающие колебания точки

Материальная точка, совершая колебания в реальных условиях, испытывает сопротивление движению (трение, сопротивление среды и т.п.). Это означает, что кроме восстанавливающей силы, направленной к центру колебаний, на точку действует сила сопротивления, всегда направленная в сторону, противоположную направлению движения точки.

Сила сопротивления при малых скоростях прямо пропорциональна первой степени скорости точки:

,

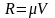где 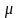– постоянный коэффициент.

Наличие сопротивления среды на технических схемах изображается с помощью демпфера.

Он представляет собой цилиндр, наполненный вязкой жидкостью, в котором движется поршень.

Дифференциальное уравнение движения материальной точки в проекции на ось Х

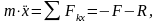
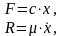
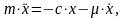
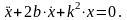(3.7.1)

где .

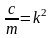Величина k является частотой свободных колебаний точки. Коэффициент b характеризует сопротивление среды.

Уравнение (3.7.1) является дифференциальным уравнением движения материальной точки под действием восстанавливающей сила и силы сопротивления, пропорциональной скорости. Это уравнение является однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

Отметим свойства затухающих колебаний:

1. При наличии сопротивления среды, пропорционального скорости движения точки, колебания затухают по закону геометрической прогрессии.

2. При наличии сопротивления среды частота колебаний убывает (по сравнению со свободными колебаниями), а их период увеличивается.

7. Вынужденные колебания точки при отсутствии сопротивления среды

Вынужденные колебания совершает материальная точка, на которую, кроме восстанавливающей силы, действует сила, периодически изменяющаяся во времени, называемая возмущающей силой.

Рассмотрим простейший, но практически очень важный случай, когда возмущающая сила 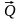изменяется по гармоническому закону

,

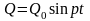Составим дифференциальное уравнение движения точки:

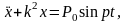(3.8.1)

где .

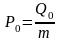Уравнение (3.8.1) представляет собой дифференциальное уравнение вынужденных колебаний при отсутствии сопротивления. Это уравнение является линейным неоднородным уравнением второго порядка, общее решение которого имеет вид

, (3.8.2)

где 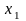– общее решение однородного уравнения 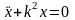; 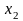– частное решение уравнения (3.8.1).

Из предыдущих расчетов известно, что 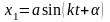(3.8.3).

В соответствии с видом функции правой части уравнения (3.8.1) частное решение при условии, что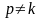 , будем искать в виде:

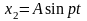, (3.8.4)

где А – неизвестная постоянная.

Для определения значения A вычисляем вторую производную уравнения (3.8.4):

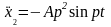(3.8.5)

Подставим в уравнение (3.8.1) уравнения (3.8.4) и (3.8.5). Получим, что 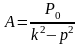(3.8.6).

Таким образом, общее решение уравнения (3.8.1) примет вид

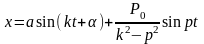. (3.8.7)

Постоянные а и α зависят от начальных условий.

Уравнение (3.8.7) показывает, что точка М совершает сложное движение, складывающееся из двух гармонических колебаний: свободных колебаний и чисто вынужденных колебаний точки.

Вынужденные колебания малой частоты 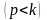не зависят от начальных условий и определяются условием

.

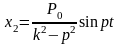При условии вынужденных колебаний большой частоты

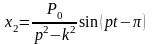. (3.8.8)

Из уравнения (3.8.8) следует, что при 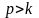фаза вынужденных колебаний отстает от фазы возмущающей силы на величину π.

При 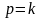, т.е. при равенстве частот свободных и вынужденных колебаний, имеет место явление, называемое резонансом. В этом случае частное решение дифференциального уравнения (3.8.1) имеет вид

. (3.8.9)

Из (3.8.9) видно, что в случае p=k размахи вынужденных колебаний возрастают пропорционально времени.

Коэффициент динамичности определяется по формуле

,

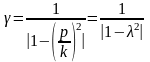где 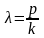– коэффициент расстройки частот.

Коэффициент динамичности 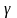характеризует динамические свойства колеблющейся системы, т.е. ее чувствительность к динамическим воздействиям.