6.Тройной интеграл.

Чтобы ввести понятие тройного интеграла, предварительно рассмотрим задачу о нахождении массы тела переменной плотности.

Пусть в системе координат Оxyz (рис. 2.18) задано некоторое ограниченное тело U с переменной плотностью γ=f(x;y;z)>0, (x;y;z) U.

Требуется приближенно вычислить массу этого тела.

Для этого разрежем это тело на n "достаточно мелких частей" ΔU_i, i=1,2,...,n.

 

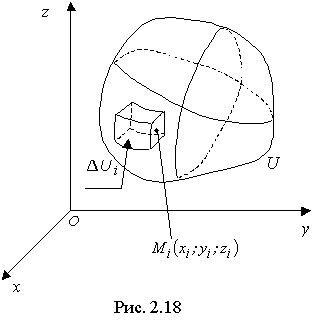
Внутри этого "кусочка" можно принять, что γ ≡ const=f(M_i), где M_i(x;y;z) - некая "средняя" точка в ΔU_i.

Обозначим объём "кусочка" ΔU_i через ΔV_i, тогда масса "кусочка" ΔM_i: ΔM_i≈f(M_i)·ΔV_i. А для всего тела: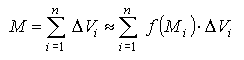

√ получена интегральная сумма.

Затем переходим к пределу при n ∞ и ΔV_i 0, i=1,2,...,n и получаем: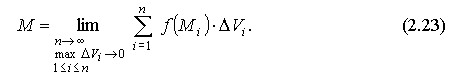

Если предел (2.23) интегральной суммы существует, то он называется тройным интегралом от функции f(x;y;z) по объему U и обозначается: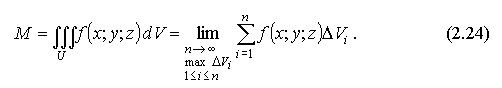

После этого можно сформулировать более точное и общее определение тройного интеграла.

Определение

Пусть f(x;y;z), (x;y;z) U - произвольная функция трех переменных, U - ограниченная трехмерная область.

Разобьем U произвольным образом на части ΔU₁, ΔU₂,...,ΔU_n. В каждой из них возьмем произвольную точку M_i(x_i;y_i;z_i) U_i и составим интегральную сумму:

Если существует предел интегральной суммы: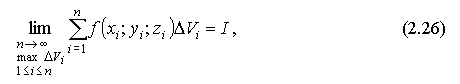

не зависящий от способа разбиения U на n частей ΔU₁, ΔU₂,...,ΔU_n, а также от произвола в выборе точек M_i U_i, то этот предел I обозначается через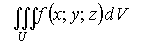  и называется тройным интегралом от функции f(x;y;z) по объёму U. При этом функция f(x;y;z) называется интегрируемой по U.

Теорема

Если f(x;y;z), (x;y;z) U непрерывна, то она интегрируема по U.

 

Определение

Тройные интегралы от непрерывных функций называются собственными тройными интегралами (или просто тройными интегралами), а тройные интегралы от разрывных функций - несобственными тройными интегралами.

В дальнейшем считаем, что все появляющиеся в тексте функции (если это не оговорено особо) интегрируемы по объёму.

7.Свойства тройного интеграла.

2.11. Свойства тройного интеграла

1. Физический смысл тройного интеграла

Если f(x;y;z)>0 на U, то масса M тела переменной плотности γ=f(x;y;z) вычисляется по формуле  

2.Объём тела:

 

Доказательство

Так как f(x;y;z)=I>0 на U, то - масса тела с плотностью γ=1.

Поэтому M=γ·V=1·V=V. В итоге I=V, что и требовалось доказать

3.

4.

5.

Если U=U₁ U₂, где U₁ и U₂ не пересекаются, то

6.

Если известны наименьшее m и наибольшее M значения непрерывной функции f(x;y;z), (x;y;z) U в области U, то тройной интеграл оценивается так:

7. Теорема

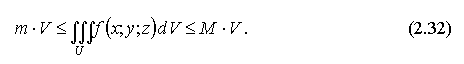
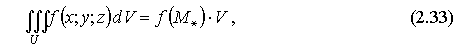(о среднем значении для тройного интеграла): где M_* - некая "средняя" точка области U, f(x;y;z) - непрерывна в U.

Доказательство

Используем свойство (6):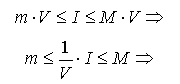

Число I/U - является промежуточным значением непрерывной функции f(x;y;z), поэтому существует точка M_*, такая, что

  в итоге , что и требовалось доказать.

доказать.

 ***********************