40. Степенной ряд. Интервал и радиус сходимости степенного ряда.
Степенным рядом называется функциональный ряд вида:
(1)
где
–
постоянные числа, называемые коэффициентами
ряда.
Теорема (Абеля)
1) Если степенной ряд сходится при некотором значении , то абсолютно сходится при всяком значении , для которого справедливо .
2) Если степенной ряд расходится при некотором значении , то он расходится при всяком : .
Заметим,
что теорема Абеля позволяет судить о
расположении точек сходимости и
расходимости степенного ряда.
Действительно, если точка х0
– точка сходимости, то интервал
заполнен
точками абсолютной сходимости. Если
–
точка расходимости, то вся бесконечная
полупрямая вправо от точки
и
вся полупрямая влево от точки –
состоит
из точек расходимости. Из этого можно
заключить, что существует число R>0,
что при
мы
имеем точки абсолютной сходимости, а
при
–
точки расходимости.
Интервалом
сходимости
степенного ряда называется такой
интервал от –R
до R,
что для всякой точки х,
лежащей внутри этого интервала, ряд
сходится при том абсолютно, а для точек
х,
лежащих вне его, ряд расходится (рис.
1). Число R
называется радиусом сходимости степенного
ряда.
Рис. 1. Интервал сходимости степенного ряда
На концах интервала (т.е. при х = R, х = –R) вопрос о сходимости или расходимости остается не ясным. И для конкретного ряда решается индивидуально. Отметим, что у некоторых рядов интервал сходимости вырождается в точку R = 0, у других охватывает всю ось (R = ¥).
41. Свойства степенных рядов.
Теорема (Абеля)
1) Если степенной ряд сходится при некотором значении , то абсолютно сходится при всяком значении , для которого справедливо .
2) Если степенной ряд расходится при некотором значении , то он расходится при всяком : .
Заметим, что теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если точка х0 – точка сходимости, то интервал заполнен точками абсолютной сходимости. Если – точка расходимости, то вся бесконечная полупрямая вправо от точки и вся полупрямая влево от точки – состоит из точек расходимости. Из этого можно заключить, что существует число R>0, что при мы имеем точки абсолютной сходимости, а при – точки расходимости.
42. Ряды Тейлора и Маклорена. Разложение функций в ряд Тейлора.
Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Определение
Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд
называется рядом Тейлора функции f в точке a. В случае, если a = 0, этот ряд также называется рядом Макло́рена
Свойства
Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например:
Ряды Маклорена некоторых функций
Экспонента:
Натуральный
логарифм
для
всех
Биномиальное разложение:
для
всех
и
всех комплексных
где
В частности:
Kвадратный корень:
для
всех
для
всех | x
| < 1
Конечный геометрический ряд:
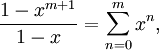для
всех
Тригонометрические функции:
для
всех
для всех
для всех
для
всех
43.Разложение функций в ряд по степеням x.
формула
ряда Маклорена (1)
1.
.
Имеем
;
.
Тогда
по формуле (1)
.
Областью
сходимости данного ряда является вся
числовая прямая, т.е.
.
2.
.
Имеем
,
откуда
и
т.д.
Очевидно,
что производные четного порядка
,
а нечетного порядка
,
где
.Поэтому
по формуле (1) имеем
.
Область сходимости ряда .
3.
.
Рассматривая аналогично предыдущему,
получим
.
Область
сходимости ряда
.
4.
,
где
–
любое действительное число.
Имеем
При
получим
Тогда по формуле (1) имеем
.
Интервал
сходимости ряда
(на
концах интервала
сходимость
зависит от конкретных значений
).
5. для всех
6. для всех